算法笔记1 复杂度分析

最新推荐文章于 2024-05-13 00:03:25 发布

阿德罗斯

最新推荐文章于 2024-05-13 00:03:25 发布

阅读量350

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/qq_37393071/article/details/86515717

本文介绍了复杂度分析在评估算法效率中的重要性，阐述了大O表示法的概念，并详细讲解了时间复杂度分析的三个方法：忽略常数、低阶项和系数，关注最大量级，以及嵌套代码的复杂度计算。同时，文章讨论了时间复杂度的四种情况：最好、最坏、平均和均摊时间复杂度，以帮助读者深入理解算法的性能表现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

微信公众号：珷玞的日常

复杂度分析是衡量算法快慢标准，这个标准很大程度上能衡量一个算法的优劣。所以在数据结构和算法最开始，复杂度分析的学习是很重要的。

为什么需要复杂度分析？

在许多算法书中都有这样一个名词，叫「事后统计法」，即通过监控代码的运行过程来得到算法的运行时间和占用的内存大小。但是显然这种方式有着很大的弊端：

测试结果非常依赖测试环境 不同的机器，硬件设施不同就可以造成代码运行时间的不同。即使是同一台机器，不同的编译器运行同一段代码时间也不尽相同。
测试结果受数据影响较大
例如在排序中，输入如果是有序的，那么运行时间就会比输入无序的结果短；另外输入数据规模过小也可能会无法真实的反映算法性能。

所以，我们需要一个不需要具体测试的方法，来达到估算算法执行效率的目的，这就是复杂度分析。

大O表示法

以一段代码为例：

# 1-1
def sum(int n):
a = 1
for i in range(n):
a += i
print(a)

这是一段很简单的累加程序，这里我们将执行每条语句的时间看成相同的。然后记录每条语句需要执行的操作数为：1+n+n+1 = 2+2n 。使用大 O 复杂度表示法表示为 O(2+2n)，也就是说，大 O 表示法并不是真的记录代码的运行时间，而是通过操作数来反映执行时间随数据规模增长的变化趋势。

时间复杂度分析的三个使用方法

1.只关注循环次数最多的一段代码
由于大O表示法只是表示一种变化趋势，所以我们通常会忽略掉公式中的常数、低阶、系数，只记录最大阶的量级。例子 1-1 时间复杂度就可以简化为 O(n)。
2.总复杂度等于量级最大的那段代码的复杂度

# 1-2
def s(int n):
a = 0
for i in range(n):
a += i
for i in range(n):
for j in range(n):
print(i+j)
print(a)

以上述代码为例，第一个 for 循环量级为 n，第二个嵌套循环量级为 n^2，代码执行的操作数为 2+n+n^2，总复杂度为 O(n^2)。

3.嵌套代码复杂度等于嵌套内外代码复杂度的乘积

这部分比较简单，不在此赘述。

时间复杂度分析的四种情况

# 1-3
def find(list s,int n,int x):
int i = 0
int pos = -1
for i in range(n):
if(s[i] == x):
pos = i
break
return pos

1.最好、最坏时间复杂度

顾名思义，最好时间复杂度就是在最理想的情况下，执行这段代码的时间复杂度。在 1-3 中，当所寻找的 x 在 s 的第一个位置时，时间复杂度是O(1)，这就是最好时间复杂度。

最差时间复杂度就是在最糟糕的情况下，执行这段代码的时间复杂度。在 1-3 中，当 x 在最后一个位置时，代码就需要运行完整个循环，时间复杂度为O(n)。

2.平均情况复杂度

在平时的数据中，最好情况复杂度和最坏情况复杂度发生的概率不大。为了更好的表示平均情况时间复杂度，平均情况复杂度就此诞生。就代码 1-3 而言，想要查找的变量 x 在数组中的位置，有 n+1 种情况：在数组的 0~n-1 位置上或者是不在数组中。我们将每种情况下，每次查找需要的操作数加起来，除以 n+1，就可以得到平均情况复杂度。即：

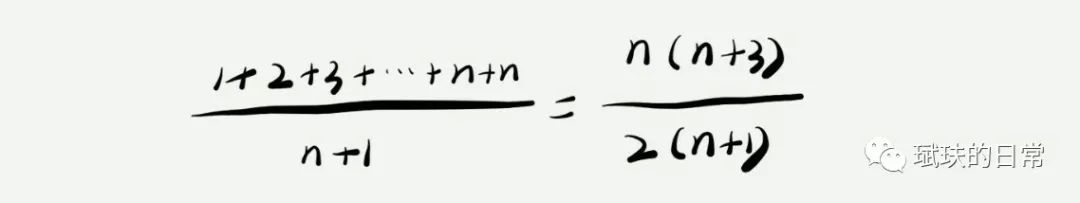
3.均摊时间复杂度

均摊时间复杂度是应用在程序循环条件带有规律时，可以将一个周期内的各自时间复杂度求取平均值，以此作为这个程序的时间复杂度，也就是均摊时间复杂度。

# 1-4
count = 0
def insert(list s,int count,int x):
if (count = len(s)):
int sum = 0
for i in range(len(s)):
sum += i
s[0] = sum
count = 1
else:
s[0] = x
++count

在上边的代码中，实现了向数组插入元素的功能。可以看到，当 count == len(s) 时，会执行 if 的内容，时间复杂度为：O(len(s))；当 count 处在 0~len(s)-1 之间，执行插入操作,时间复杂度为：O(1)。所以每 n+1 次操作构成一个周期。均摊时间复杂度为：O(1)。