HDU-3308-线段树合并-求最大连续子串

!

题目链接

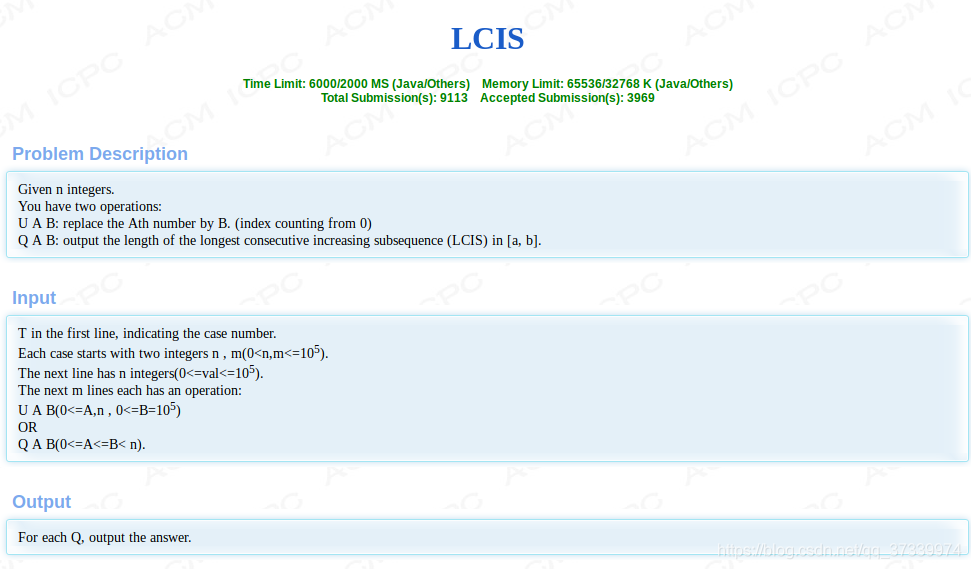
题意：

​ 给定一段区间求 最长连续上升序列长度

​ 两个操作 Q 操作区间查询最长连续上升子序列 U操作 单点更新

题解：

​ 一般的区间合并问题，我算是发现了，都要维护三个基本参数

​ 从左端开始的 从右端开始的 中间最大的

​ 所以这个题 也不例外 维护左端开始的最长 和右端结束的最长 还有区间最长

​ 然后 在记录一下这个区间的左右端点值 在合并的时候 需要比较

​ 主要是如何pushup 首先往上更新的时候 最长的肯定是左右的最大的

​ 然后 左端 判断是否贯穿 贯穿就是 左儿子右端点大于 右儿子左端点 这个时候

​ 左端连续 要加上右儿子的左端连续

​ 同理 右端连续也是这样 然后就可以了

​ 然后 查找的时候 同样遵守之前的道理 你的区间要是分开的时候要判断一下

​ 你分开的区间 左儿子的右端点和右儿子的左端点的大小比较一下

​ 如果可以连续 我们比较一下 左右儿子的最大和 还有这个区间大小

​ 就是你不能超过这个区间的大小和之前的找01 最长1的那个是一个道理

​ 然后比较一个最大值就可以了

ps : 总感觉最正统的线段树往下递归的时候 都应该分三个写诶 以前两个的写法有点偷懒

AC代码

#include<bits/stdc++.h>
#define N 100005
using namespace std;
struct node
{
    int l,r;
    int ls,rs;
    int lsum,rsum,sumb;
};
node shu[N<<2];
int a[N];
void pushup(int rt)
{
    shu[rt].ls = shu[rt<<1].ls;
    shu[rt].rs = shu[rt<<1|1].rs;
    shu[rt].sumb = max(shu[rt<<1].sumb,shu[rt<<1|1].sumb);
    if(shu[rt<<1|1].ls>shu[rt<<1].rs)
    {
        shu[rt].sumb = max(shu[rt].sumb,(shu[rt<<1].rsum + shu[rt<<1|1].lsum));
    }
    shu[rt].lsum = shu[rt<<1].lsum;
    if(shu[rt].lsum == (shu[rt<<1].r - shu[rt<<1].l+1) && shu[rt<<1].rs<shu[rt<<1|1].ls)
    {
        shu[rt].lsum += shu[rt<<1|1].lsum;
    }

    shu[rt].rsum = shu[rt<<1|1].rsum;
    if(shu[rt].rsum == (shu[rt<<1|1].r - shu[rt<<1|1].l+1) && shu[rt<<1].rs<shu[rt<<1|1].ls)
    {
        shu[rt].rsum += shu[rt<<1].rsum;
    }

}
void build(int rt,int l,int r)
{
    shu[rt].l = l,shu[rt].r = r;
    if(l==r)
    {
        shu[rt].ls = shu[rt].rs = a[l];
        shu[rt].lsum = shu[rt].rsum = shu[rt].sumb = 1;
        return ;
    }
    int mid = (l+r)>>1;
    build(rt<<1,l,mid);
    build(rt<<1|1,mid+1,r);
    pushup(rt);
}
void update(int rt,int pos,int val)
{
    int L = shu[rt].l ,R = shu[rt].r;
    if(L==R&&L==pos)
    {
        shu[rt].ls = shu[rt].rs = val;
        return;
    }
    int mid = (L+R)>>1;
    if(pos<=mid) update(rt<<1,pos,val);
    else update(rt<<1|1,pos,val);
    pushup(rt);
}
int Find(int rt,int l,int r)
{
    int L = shu[rt].l, R = shu[rt].r;
    if(l<=L&&R<=r)
    {
        return shu[rt].sumb;
    }
    int ans = 0;
    int mid = (L+R)>>1;
    if(l<=mid) ans = max(ans,Find(rt<<1,l,r));
    if(r>mid) ans = max(ans,Find(rt<<1|1,l,r));
    if(shu[rt<<1].rs < shu[rt<<1|1].ls && l<=mid && r>mid )
    {
        ans = max(ans , (min(shu[rt<<1].rsum,mid-l+1)+min(shu[rt<<1|1].lsum,r-mid)));
    }
    return ans;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n,m;
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
        }
        memset(shu,0,sizeof(shu));
        build(1,1,n);
        while(m--)
        {
            char s1[10];
            int l,r;
            scanf("%s%d%d",s1,&l,&r);
            if(s1[0]=='Q')
            {
                l++,r++;
                int x1 = Find(1,l,r);
                printf("%d\n",x1);
            }
            else
            {
                l++;
                update(1,l,r);
            }
        }
    }
}

作者拥有版权，请注明出处转载！

如果觉得有什么疑惑或者博主代码有什么问题，可以通过关于我，加我QQ联系 ，感谢。