CMU 15-213 CSAPP

导论

[root@zhr ~]# gdb
GNU gdb (GDB) Fedora 8.1-11.fc28
Copyright (C) 2018 Free Software Foundation, Inc.
License GPLv3+: GNU GPL version 3 or later <http://gnu.org/licenses/gpl.html>
This is free software: you are free to change and redistribute it.
There is NO WARRANTY, to the extent permitted by law.  Type "show copying"
and "show warranty" for details.
This GDB was configured as "x86_64-redhat-linux-gnu".
Type "show configuration" for configuration details.
For bug reporting instructions, please see:
<http://www.gnu.org/software/gdb/bugs/>.
Find the GDB manual and other documentation resources online at:
<http://www.gnu.org/software/gdb/documentation/>.
For help, type "help".
Type "apropos word" to search for commands related to "word".
(gdb) print 40000 * 40000
$1 = 1600000000
(gdb) print 50000 * 50000 
$2 = -1794967296
(gdb) 

上面我们打开GDB 输入4w * 4w 是正数，而5w * 5w是负数为什么？5w * 5w是正数相乘不可能为负
是程序出错了吗？不是的，因为我们这台计算机默认他为32位也就是4个字节的最大表示4294967296个数字，但是在DGB中他是有符号的，32位字符表示范围为-2147483648~2147483647，但是我们的 5w * 5w 等于2500000000超出了最大表示2147483647，352516352个数字，再拿-2147483648加上352516352正好等于-1794967296（超出范围后从最左边的数字重新开始计算超出的范围）

(gdb) print 300*400*500*600
$6 = 1640261632
(gdb)   
/*  300*400*500*600不可能出现个数为，十数位，百数位，为什么我们的计算结果出现了？因为他溢出了*/

(gdb) print 1e20 - 1e20 +3.14
$7 = 3.1400000000000001
(gdb) print 1e20+(-1e20+3.14)
$8 = 0
(gdb) 
/*我们知道整数可以满足加法的结合律，但是我们这个例子从数学的角度来说2个式子都是一样的，但是我们的计算结果不一样*/

typedef struct {
	int a [2]; 
	double d;  
}struct_t;  
double fun(int i)  
{
	volatile struct_t s ; 	//volatile 的作用 是作为指令关键字，确保本条指令不会因编译器的优化而省略，且要求每次直接读值。
	s.d = 3.14;  
	s.a[i] = 1073741824;  
	return s.d;
}  
/*当我们的i等于0或者1的时候他会输出正常  
fun(0) = 3.14；  
fun(1) = 3.14;  
但是当我们的i大于1的时候就出现异常了  
fun(2) = 3.1399986664856  
fun(3) = 2.00000061035156
fun(4) = 3.14
fun(5)  = 3.14
fun(6)  segmentation fault  
*/

为什么上述的代码会出现这样？我们输出的是s.d也就是浮点数，我们输入的只改变数组，这样的，因为当我们的数组当i等于2的时候就越界了，我们的c/c++并不会检查他，c/c++很乐意我们访问内存 ，当数组越界后他会影响后面的变量，在我们例子中是s.d这个double变量，因为我们结构在内存中存储的位子很奇特 如下图

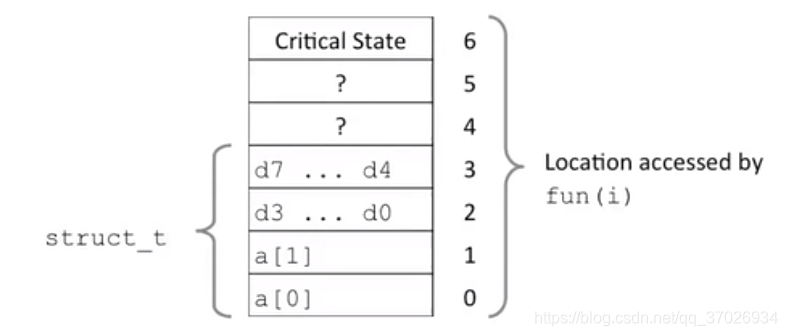
当我们的输入越界后，比如输入i = 2，他就影响到了他后面存储的double类型只到输入4，5，我们也不知道它里面存储的是什么，如果这样改变了就非常的可怕，再输入到6的时候，这一片内存已经被操作系统分配给其他的应用了，我们改变他就会由操作系统报错，禁止你的操作也就是 segmentation fault

计算机位

二进制 与位

最开始我们使用的10进制表示，但是10进制表示电子管非常的复杂，所以到了1948年人们又使用2进制表示，其中二进制只有0和1，0和1都表示某一个阈值之间的范围，0表示低压，1表示高压，他们相互转换

在计算机世界中用2进制表示所有数字
平常2进制数动不动就32位64位这样非常的长所以我们使用16进制表示他
16进制表示2进制的规则就是，2进制4个为一组，每一组都转换成16进制

我们内存中的虚拟地址是由机器的字长决定的，字长的大小是64或者32或者16等，也就是我们计算机的处理器32位他的字长就是32位，64位处理器，他的字长就是64位，而64位操作系统和32位操作系统是为了匹配64位处理器或者32位处理器。
注意的是64位的pc可以跑32位os，虽然浪费，但是64位os不可能跑在32位pc上，因为他的内存总线，就是32位的，64位os一次传64位的数据。

字长：字长分很多种类
机器字长： CPU一次运算处理的二进制位数。
指令字长： 计算机指令字的位数。
数据字长： 计算机数据存储所占用的位数。
存储字长： 存储器中一个存储单元(存储地址)所存储的二进制代码的位数，即存储器中的MDR的位数。
一般我们说的字长就是机器字长

and，or，exclusive OR（异或），取反

and就是当2个数都是为1的时候才为1，其他时候为0
or就是当2个数有一个为1的时候就为1，其他为0
^就是当2个数相同的时候就为0，否则就为1，
~就是取反
千万不要和&&和||搞混，前一个表示a&&b，a和b都为真才返回真，a||b，a和b其中有一个为真则返回真，我们最开始讲的是bit位操作

右移左移

右移和左移分为一下4种
算数左移
逻辑左移
算数右移
逻辑右移

其中算数左移和逻辑左移相同都是往左移动后右边填充0
逻辑右移也是的，往右边移动左边填充0
算数右移是往右移动往左添加符号相关的位，比如是负数最高位为1，比如11001001，右移一位为11100100，最左边高位填充的是符号位1

源码，反码，补码

首先先说结论计算机所有的数字都是以补码存储的
因为补码可以直接将比特位使用cpu中的加法器进行相加，不用额外的模拟电路，
正数的补码是他本身，而负数的补码为他本身取反加一（取反不包括第一个符号位）

符号扩展和无符号扩展

一个8位int扩展成16位int，首先判断这个数是否为signed还是usigned，unsigned不用说，8位扩展成16位前面全部都为0，但是如果是有符号，为负数那么第一个高位为1，如果扩展的话前面都置为1比如，10000011，这个是一个8位signed int（为负），扩展成16位就为，11111111 10000011
为什么？？？
这里我们注意一个知识点，signed int 为负的4位2进制，1110，把他转化成10进制和signed大部分一样就只有一点不一样，那就是最高位位负数，
如果1110为无符号数，他这样化成10进制

1*2^3+1*2^2+1*2^1+0*2^0=14

如果1110为signed，可判断他为负，因为第一个数字（高位）为1，他这样化成10进制

-1*2^3+1*2^2+1*2^1+0*2^0=-2  
我们将他扩展成6位，而且按照以上的法则“有符号扩展前面高位都置为1”，得到以下式子  
-1*2^5+1*2^4+1*2^3+1*2^2+1*2^1+0*2^0=-2 
//符号没有变说明成功！

符号截断和无符号截断

首先我们将2进制无符号数阶段

10101010	//将此2进制数左边高位截断2位成  
  101010  

这中间有个式子可以由原unsigned 二进制数得到被截取后的unsigned int,公式如下

10101010=a	//a为次二进制数字的10进制， 
  101010=b 		// b为次二进制数字的10进制，k为b二进制的长度，也就是有多少位  
a%(2^k)=b	//%为取模，k也就是被截取后还有多少位

有符号截断

unsigned addition

假设我们有2个unsigned的数13和5我们将他们的2进制相加，假设他们2进制只有4位
13 = 1101
5 = 0101
将上述2个4位2进制相加为
10010，但是我们一共只有4位所以我们的计算结果超出了一位，所以最高位1被截掉，只剩0010，最后结果位2，这也叫做溢出

如果我们有2个数一个为5（0101），一个为-3补码为（1101）两个相加为10010，但是只有4位所以截取最高位1得到0010为2，所以我们的补码可以直接参与加减法
所以我们的数字绝大多数都用补码

如果我们有2个负数一个为-3补码为1101，一个为-6补码为1010，把他们相加为10111，除去最高位1得到0111，为7，我们所知-3加上-6为-9不是7，但是我们直接2进制补码相加为7，因为他们溢出了，他因该是-9但是我们不能用4位2进制表示他所以溢出
总结我们如果2个整数补码相加等于负数，说明他们正溢出了，如果2个负数补码相加等于正数，他们负溢出了

比特位乘法

我们直到比特位加法就是取其补码直接加，我们再回顾一下补码的知识
首先正数的补码就是其本身，负数的补码为其取反加1，那么负数的源码怎么表示？
比如-0101为真值，其源码为1101，也就是最高位为负数（1）
此时我们有2个数-3和3，我们要计算他们的乘机，使用二进制运算，其运算方法如下
3的源码为011，其补码为其本身
-3的真值为-011，其原码为111，补码取反加一（除了符号位）得到101，我们将其相乘

		101	#-3
		011	#-3
________________________ 
     111101		#第一行为-3最低位1乘以上面的3位，并且要补位，补的位数是N，总大小位2N（N为位数，我们101和011都只有三位所以布三位，并且如果为1则布的值为前面的数，如果为0则就补0，上面最后一个数为1*1则补三个1）
     11101			#与上面一样但是左边和上面对其，右边空一格
     0000 			#与上面一样但是左边和上面对其，右边空一格
————————————————————————— 
    1110111 		#相加得到1110111
——————————————————————————
     110111	#与上面对其，舍弃最左边的1，得到最终结果110111为-9

算法图解如下

注意无符号和有符号乘机的时候有符号在上无符号在下，其他直接乘

位移和乘法，除法

unsigend

我们有一个unsigned无符号二进制数0110，他为6，他左移一位为1100，为12，所以左移一位为乘以2，我们的位移比乘法运算更加的简洁，通常位移只需要1个时钟周期，而乘法需要三到四个，但是我们现代编译器都会给程序调优，乘法会被编译器调优成位移，我们通过向左位移得到一个公式

u << k 等于 u*2^k

我们除法就是往右位移

u>>k 等于 u/2^k
比如上面的0110（6）右移一位为0011（3），但是我们再往右位移一位为0001（1），为啥不是1.5？因为整数不
会输出小数，而是约等，并且往0靠（注意不是四舍五入）

signed

signed的情况比signed的情况复杂多得多了，如果signed是正数那么就和unsigned一样如果为负数因为涉及到符号位所以我们要特别考虑
如果signed的符号为负也就是最高位为1，那么他在除法的时候往右位移一位，但是最高位要补1，不再补0，例如

1010为-6的补码 
-6/2=-3，则1010往右位移一位并且高位补一，为1101为-3的补码 
如果我们再往右位移一位，高位补一得到1110为-2的补码，我们理应的带-1.5就算约等于也是往0靠其也就是-1.这种情况我们可以加一个偏移位也就是加上1个bit，计算如下 
1101 + 0001 = 1110 （加上一个bit的偏移位）
1110 >> 1 = 1111(往右位移一位得到-1的补码)

如果是有符号乘法的时候
32:46

扩充1：

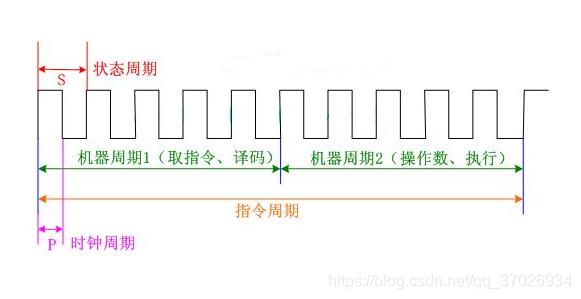
时钟周期：一个时钟脉冲所需要的时间。在计算机组成原理中又叫T周期或节拍脉冲。是CPU
和其他单片机的基本时间单位。它可以表示为时钟晶振频率（1秒钟的时钟脉冲数）的倒数（也
就是1s/时钟脉冲数，比如1/12MHz），对CPU来说，在一个时钟周期内，CPU仅完成一个最基
本的动作。时钟脉冲是计算机的基本工作脉冲，控制着计算机的工作节奏。时钟频率越高，时
钟周期就越短，工作速度也就越快。时钟周期在CPU的描述里也叫节拍，即将一个机器周期划
分成若干个相等的时间段，每一段仅完成一个基本操作，用一个电平信号宽度对应。举例：
（个人理解）工作频率为100MHZ的芯片的时钟周期为10000ns，理解为1s(10的9次方ns)内的
时钟周期个数为10的8次方，所以每个时钟周期的时间长为10的9次方ns/10的8次方个时钟周
期，结果为10ns。

总线周期：cpu从内存中读取指令，向内存中存取数据，对外设端口读写数据，执行总线周
期，总线周期通常包含4个T状态：T1，T2，T3,T4。所谓一个T状态就是一个时钟周期。它是
CPU执行操作的最小时间单位。

机器周期：通常用从内存中读取一个指令字的最短时间来规定CPU周期（机器周期），也即
CPU完成一个基本操作所需的时间。通常一个机器周期包含12个时钟周期，在8051系列单片机
的一个机器周期由6个S周期（状态周期）组成。 一个S周期=2个节拍（P），也就是一个状态
周期包含2个时钟周期，所以8051单片机的一个机器周期=6个状态周期=12个时钟周期。又称
CPU的工作周期或基本周期，总线周期。

指令周期：执行一条指令所需要的时间，是从取指令、分析指令到执行完指令所需的全部时
间，计算机中，常把一条指令的执行过程划分为若干个阶段，每一个阶段完成一项工作。每一
项工作称为一个基本操作，完成一个基本操作所需要的时间称为机器周期，所以一个指令周期
一般由若干个机器周期组成。指令不同，所需的机器周期也不同，比如一个复杂指令可能需要
很多个机器周期才能完成，而每个机器周期又由多个时钟周期完成。

扩充2：
逻辑右移就是不考虑符号位，右移一位，左边补零即可。
算术右移需要考虑符号位，右移一位，若符号位为1，就在左边补1,；否则，就补0

内存面向字节的表示

在我们的脑海中内存是一个巨大的字节数组 ，如果在64位机器上内存由64位表示，但是我们实际在机器上使用的最大内存地址为47位，逻辑上程序认为你的计算机有那么大的字节的内存，而且他不是都能访问，因为计算机只能他访问一些空间，如果程序试图访问其他的空间则会报错（segmentation fault）

我们所说的64位机器，一般是指处理64位值，和算数运算，并且他的指针或者说地址是64位的

字长:字长并没有确切的定义，硬件本身并不一定定义字长大小，是硬件和编译器一起决定的程序中使用的字长大小是多少

大端序小端序

首先我们的计算机内存存储有2中方式大端序和小端序，
小端序:第一个字节是最低有效字节，然后直到最大的字节位于高位 （intel x86）
大端序:大端序正好反过来
大端序和小端序的英文名出自于小说<<格列佛游记>>

在世界上同时存在大端序和小端序机器，我们现在越来越难找到大端序机器
arm处理器（手机上的）他可以处理大端序也可以处理小端序，如果arm处理器上运行标准操作系统的时候，他会用小端序来运行
以前的sun microsystems公司推出的鼎鼎大名的处理器power pc，他就是使用大端序
现代的互联网中还有一个地方频繁使用大端序就是：当internet发送32位数据包的时候，他是以大端序发送的，在网络端口你必须要在2者之间转换