m数据结构 day18 查找（一）无序表查找（线性查找），有序表查找（二分查找，插值查找， 斐波那契查找）

查找,也叫做 搜索，是一个非常常用，操作极为频繁的操作。

比如当我们写完一篇博客，载有这篇博客的网页就会被上传到优快云网站的主机上，然后各大搜索引擎公司，比如Google，百度等，就会抓取到这个新网页（爬虫），并把它存入他们公司自己的网页数据库，然后搜索引擎公司会对这个网页进行分析，比如全文检索提取有效信息并存入索引数据库，提取网页链接存入链接数据库。并且这些搜索引擎公司还会定期再去优快云网站看看我的这个网页的地址是否变化，对它的链接数据库做定期的维护。

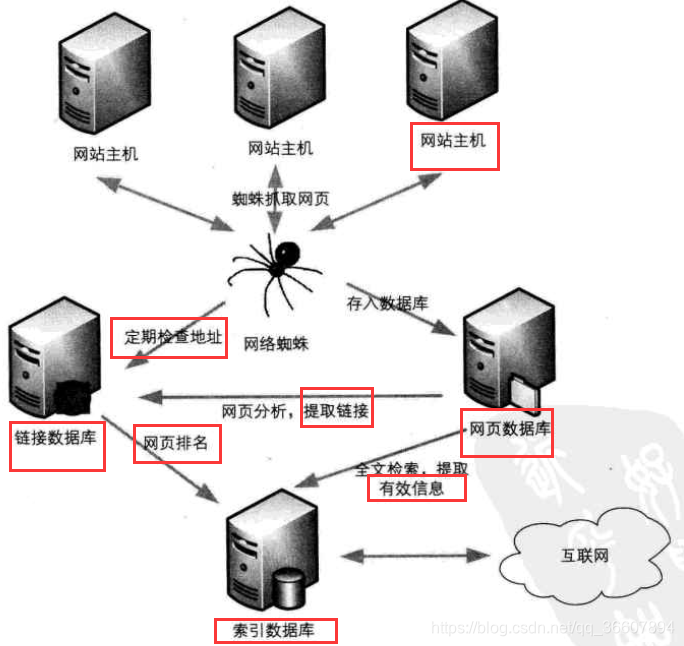
当你输入关键词，点击搜索之后，搜索引擎的查找算法就会带着你的关键词奔向索引数据库，检索到所有包含关键词的网页，并按照这些网页的浏览次数和关联性按照一定算法对网页们进行排序，然后按照排序后的格式呈现在网页上。

概念

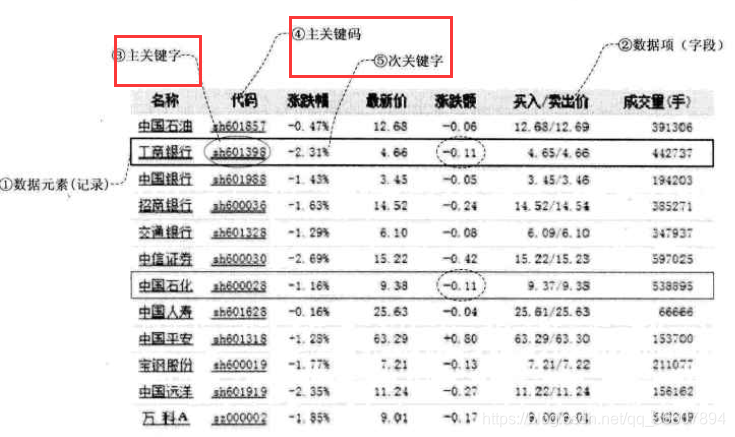
• 关键字：key, 是数据元素中某个数据项的值，又称为键值。用于标识一个数据元素或者一个记录的某个字段（标识一个记录的某个字段的关键字也叫做关键码）。

• 主关键字:primary key, 可以唯一地标识一个记录的关键字。所以不同记录的主关键字不同。

• 主关键码：主关键字所在的数据项（字段）。

• 次关键字：secondary key,可以识别多个数据元素或记录的关键字。即不能唯一标识一条记录的关键字呗。

• 次关键码：次关键字对应的数据项。
  

• 查找表: search table, 所有被查的数据所在的集合。由同一类数据元素或数据记录构成的集合。

查找表按照操作方式可以分为两大类：静态查找表，动态查找表。

• 静态查找表：static search table,只做查找操作的查找表。比如：查询某各数据元素是否在查找表中；检索某个数据元素及其属性。
• 动态查找表: dynamic search table，即不只做查找，查找的目的不只是为了查找，比如添加和删除，你要首先查找一下添加项或者删除项是否在查找表中，如果不在则可以添加，不能删除。
• 查找：searching，根据给定值，在查找表中确定一个关键字等于给定值的数据元素或记录。
• 查找结构：为了提高查找的效率，专门为查找操作设计的数据结构，是面向查找操作的数据结构。本来，查找面向的数据结构是集合，即所有被查找的数据相互之间没有关系，只是同在一个集合里，但是为了提高查找的效率，所以要为数据元素之间加点关系，比如动态查找表可以把数据元素们存储为集合以外的数据结构中，比如存在二叉查找树中，这样能够提高查找和添加删除的效率。

静态查找表还是要使用线性表结构来存储数据，因为这样可以用顺序查找算法；如果对静态查找表的主关键字排序，则可以用二分查找。
动态查找表一般用二叉查找树存储，还可以用散列表结构。

无序表查找

根据查找表中的数据记录之间的关系是否有特定顺序，查找可分为无序表查找和有序表查找。

无序表查找，即查找表的数据记录们没有任何次序，只是同处一个集合的关系。

线性查找（顺序查找）:最基本的查找技术，$O(n)$,适合用于小型数据

代码

这里是以数组存储结构和int类型关键字来示例的，实际应用中，数据还可以用栈，队列，链表等线性表数据结构存储。关键字也可以改变。

代码很简单，就是从头开始找

int Sequential_search(int *a, int n, int key)
{
   
   
	int i;
	for (i=0;i<n;++i)
		if (a[i]==key)
			return i;
	return -1;
}

时间复杂度分析：

• 最好情况：第一个就找到了，O(1)
• 最坏情况：最后一个才找到，则需要比较n次；或者最后一次都没找到,则需要n+1次比较。O(n)
• 平均情况：由于关键字在任何一个位置找到的概率是一样的，所以平均查找次数是(n+1)/2,所以最后的时间复杂度还是O(n)

代码层面的优化（值得学习发扬）：使用哨兵以减少不必要的比对，$O(n)$

这是一个很细微的代码层面的优化，真的很细微，很适合用在日常工作中的一线代码调优中。

上面的代码用for循环，每一次都要判断i是否还小于n,在n很大的时候，这个判断也会耗费很多时间。所以，优化的思路就是省略这个判断，每次不要再把i和n作比较。怎么做呢？通过加入一个哨兵。直接看代码：

int Sequential_Search2(int * a, int n, int key)
{
   
   
	int i;
	a[0] = key;//a[0]是哨兵，不用于存储数据，这是和上面代码的一大区别
	i = n;//倒着查找
	while (a[i]!=key)
		--i;
	return i;//返回0则说明查找失败
}

或

int Sequential_Search2(int * a, int n, int key)
{
   
   
	int i;
	a[n] = key;//a[0]是哨兵，不用于存储数据，这是和上面代码的一大区别
	i = 0;//顺着查找
	while (a[i]!=key)
		++i;
	return i;//返回n则说明查找失败
}

这样一改，就只需要比对数据元素和关键字了，不需要比较循环变量i和n的大小。对于很大的n,还是一笔可观的优化的。这种优化细节一定要学着点。

虽然时间复杂度还是$O(n)$,但是一定要明白，$O(n)$和$O(n)$之间绝对也是有区别的，虽然咱们用大O表示法省略了系数和低次项，但是如果真是相同复杂度的两个算法来比较的话，还是要看看那些被省略的项的。比如，成绩不用分数公布，而是公布为优秀，良好，及格，不及格等，那99和91都是优秀，有区别吗？有。优秀和优秀之间也不全是一样的。一个道理。

优缺点

• 优点：简单，不需要对静态查找表的记录进行排序等操作
• 确定：n很大时，查找效率很低，所以不适用于大型数据集，只适用于小数据。

其实，每一条数据被查找的概率是不一样的，就像之前学习霍夫曼编码，每一个字符在文本信息中的出现概率是不一样的，所以可以给大概率出现的字符更短的编码，而给小概率出现的字符较长的编码，这样可以使得平均码长更短，进而压缩数据。仅仅是考虑到了字符的出现概率，就做出了如此巨大的优化，现在也是一样，我们应该考虑到一个客观事实，那就是查找表中的多条数据，并不是以均等的概率被用户搜索查找的，一定是某些数据记录被频繁查找，而另一些则不怎么被人问津。

基于这种概率特性带来的启示，我们应该把经常被查找到的数据记录放在查找表的前面，而不经常被查找的记录放在后面，这样就可以大幅提高效率。这就是下面要说的有序表查找。

有序表查找

无序查找一定是差于有序查找的。不然图书馆为啥要给所有书编号呢？图书馆又不傻。

对线性表先做个排序，然后在查找，效率会高很多。

二分查找，$O(\log n)$，前提：顺序存储有序查找表

binary search，也叫折半查找

前提：线性表中的记录必须是关键字有序（一般从小到大的顺序）的，且线性表必须采用顺序存储，即不能用链式存储。

换句话说，二分查找必须用数组存储一个有序查找表，而不可以用单链表。

思想：取有序表的中间记录作为比较对象，如果给定值等于中间记录的关键字，则查找成功；若给定值小于中间记录的关键字，则在中间记录的左半区继续使用二分查找进行查找；若给定值大于中间记录的关键字，则在中间记录的右半区查找。重复这个过程，直到查找成功或者查找失败为止。

每次都找中间，记住找中间就对了。

代码

举个例子，从一个有11个元素的int数组中找是否有数字62，注意，数组a是排序过的哦，这是二分查找的前提，关键字必须有序，这里关键字就是数据本身

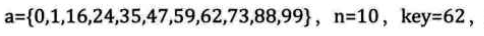
int Binary_Search(int *a, int n, int key)
{
   
   
	int low, mid, high;
	low = 1;//注意不是0哦！
	high = n;
	while (low<=high)
	{
   
   
		mid = (low + high) / 2;//整数除法
		if (key < a[mid])
			high = mid-1;
		else if (key > a[mid])
			low = mid+1;
		else
			return mid;//查找成功
	}
	return -1;//查找失败
}

• 过程：
  注意low并不是指向0！！！

如果不想多浪费第一个空间，想从0开始，则代码为：

//二分查找
int Binary_Search(int *a, int n, int s)
{
   
   
	int low=0, mid, high=n-1;
	while (low<high)
	{
   
   
	    mid = (low+high)/2 + 1;//改变在这里，很简单很好理解
	    if (s == a[mid])
	        return mid;
	    else if (s > a[mid])
	        low = mid + 1;
	    else if (s < a[mid])
	        high = mid - 1;   
	}
	if (low==high && a[low]==s)
	    return low;