目录:
-
信息量
-
熵
-
相对熵(KL散度)
-
交叉熵
-
JS散度
-
推土机理论
-
Wasserstein距离
-
WGAN中对JS散度,KL散度和推土机距离的描述
信息量:
任何事件都会承载着一定的信息量,包括已经发生的事件和未发生的事件,只是它们承载的信息量会有所不同。如昨天下雨这个已知事件,因为已经发生,既定事实,那么它的信息量就为 0。如明天会下雨这个事件,因为未有发生,那么这个事件的信息量就大。
从上面例子可以看出信息量是一个与事件发生概率相关的概念,而且可以得出,事件发生的概率越小,其信息量越大。这也很好理解,狗咬人不算信息,人咬狗才叫信息嘛。
我们已知某个事件的信息量是与它发生的概率有关,那我们可以通过如下公式计算信息量:假设X是一个离散型随机变量,其取值集合为 x ,概率分布函数P(x)=Pr(X=x) ,,则定义事件X=
的信息量为:
熵:
信息量的期望就是熵,所以熵的公式为:
假设事件X共有 n 种可能,发生的概率为
,那么该事件的熵H(X)为:
然而有一类比较特殊的问题,比如投掷硬币只有两种可能,字朝上或花朝上。买彩票只有两种可能,中奖或不中奖。我们称之为 0-1 分布问题(二项分布的特例),对于这类问题,熵的计算方法可以简化为如下算式:
相对熵(KL 散度):
相对熵又称 KL 散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x),我们可以使用 KL 散度(Kullback-Leibler (KL) divergence)来衡量这两个分布的差异。
在机器学习中,P 往往用来表示样本的真实分布,Q 用来表示模型所预测的分布,那么 KL 散度就可以计算两个分布的差异,也就是 Loss 损失值。
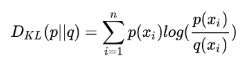
从 KL 散度公式中可以看到 Q 的分布越接近 P(Q 分布越拟合 P),那么散度值越小,即损失值越小。
因为对数函数是凸函数,所以 KL 散度的值为非负数。
有时会将 KL 散度称为 KL 距离,但它并不满足距离的性质:
-
KL 散度不是对称的;
-
KL 散度不满足三角不等式。
交叉熵:
我们将 KL 散度公式进行变形:
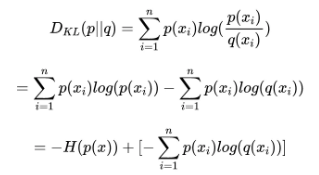
等式的前一部分恰巧就是 p 的熵,等式的后一部分,就是交叉熵:
![]()
在机器学习中,我们需要评估 label 和 predicts 之间的差距,使用 KL 散度刚刚好,即![]() ,由于 KL 散度中的前一部分 −H(y)不变,故在优化过程中,只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做 loss,评估模型。
,由于 KL 散度中的前一部分 −H(y)不变,故在优化过程中,只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做 loss,评估模型。
JS 散度:
JS 散度度量了两个概率分布的相似度,基于 KL 散度的变体,解决了 KL 散度非对称的问题。一般地,JS 散度是对称的,其取值是 0 到 1 之间。定义如下:
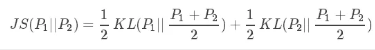
Wasserstein 距离(该部分摘自KL 散度、JS 散度、Wasserstein 距离):
KL 散度和 JS 散度度量的问题:
如果两个分配 P,Q 离得很远,完全没有重叠的时候,那么 KL 散度值是没有意义的,而 JS 散度值是一个常数。这在学习算法中是比较致命的,这就意味这这一点的梯度为 0。梯度消失了。
Wasserstein 距离度量两个概率分布之间的距离,定义如下
![]()
Π(P1,P2)是 P1 和 P2 分布组合起来的所有可能的联合分布的集合。对于每一个可能的联合分布 γ,可以从中采样(x,y)∼γ 得到一个样本 x 和 y,并计算出这对样本的距离||x−y||,所以可以计算该联合分布 γ 下,样本对距离的期望值 E(x,y)∼γ[||x−y||]。在所有可能的联合分布中能够对这个期望值取到的下界 infγ∼Π(P1,P2)E(x,y)∼γ[||x−y||]就是 Wasserstein 距离。
直观上可以把 E(x,y)∼γ[||x−y||]理解为在 γ 这个路径规划下把土堆 P1 挪到土堆 P2 所需要的消耗。而 Wasserstein 距离就是在最优路径规划下的最小消耗。所以 Wesserstein 距离又叫 Earth-Mover 距离。
Wasserstein 距离相比 KL 散度、JS 散度的优越性在于,即便两个分布没有重叠,Wasserstein 距离仍然能够反映它们的远近;而 JS 散度在此情况下是常量,KL 散度可能无意义。WGAN 本作通过简单的例子展示了这一点。考虑如下二维空间中的两个分布 和
,
在线段 AB 上均匀分布,
在线段 CD 上均匀分布,通过控制参数
可以控制着两个分布的距离远近。
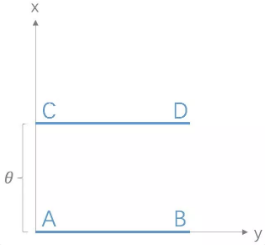
此时容易得到
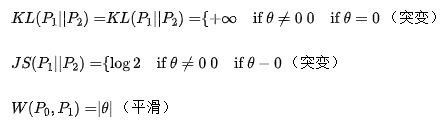
KL散度和JS散度是突变的,要么最大要么最小,Wasserstein距离却是平滑的,如果我们要用梯度下降法优化这个参数,前两者根本提供不了梯度,Wasserstein距离却可以。类似地,在高维空间中如果两个分布不重叠或者重叠部分可忽略,则KL和JS既反映不了远近,也提供不了梯度,但是Wasserstein却可以提供有意义的梯度。
WGAN中对KL散度和JS散度的描述

最优判别器:
首先根据公式1,当生成器固定时,确定最优的判别器。对判别器进行求导,并令导数为0,则:
![]()
化简得:
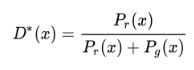
从上述公式也可以很容易看出最优判别器的特征:当![]() 且
且![]() ,最优判别器可以给出概率值0,相反,最优判别器可以给出概率值1。
,最优判别器可以给出概率值0,相反,最优判别器可以给出概率值1。
生成器损失:
普通的GAN在训练时会有一个明显问题,即如果判别器训练的太好,生成器就会完全学不动;那么当判别器为最优时,我们可以通过公式推导生成器的损失函数是怎样。










 本文深入解析信息论中的核心概念——熵、相对熵(KL散度)、交叉熵、JS散度及Wasserstein距离,阐述其在机器学习中的应用,特别是GAN模型中的作用。通过实例说明不同散度度量的优劣,强调Wasserstein距离在解决分布不重叠问题上的优势。
本文深入解析信息论中的核心概念——熵、相对熵(KL散度)、交叉熵、JS散度及Wasserstein距离,阐述其在机器学习中的应用,特别是GAN模型中的作用。通过实例说明不同散度度量的优劣,强调Wasserstein距离在解决分布不重叠问题上的优势。
















 320
320

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








