《算法图解》总结及实战

一、算法简介与二分查找法

开启算法探索之路之前，首先要了解的概念：

1.大O表示法：用来表示算法的速度有多快。这里的速度并非指时间，而是增速。

    常见的大O运行时间：（n表示操作数）

     O (log n )，也叫对数时间 ，这样的算法包括二分查找。

     O (n )，也叫线性时间 ，这样的算法包括简单查找。

     O (n * log n )，这样的算法包括快速排序。

     O (n ^2 )，这样的算法包括选择排序。

     O (n !)，也叫阶乘时间（n!为n的阶乘）,这样的算法包括旅行商问题的解决方案。

2.二分查找法用大O表示法表示为：O（logn）；

注：对数运算是幂运算的逆运算，即 log10 100相 当于问“将多少个10相乘的结果为100”。答案是两个：10 × 10 = 100。因此，log10 100 = 2。

 

二、选择排序

1.数据结构：链表

    链表的每个元素都存储了下一个元素的地址，从而使一系列随机的内存地址串在一起。

2.数据结构：数组

    数组存储连续的地址，可以通过索引下标进行访问。

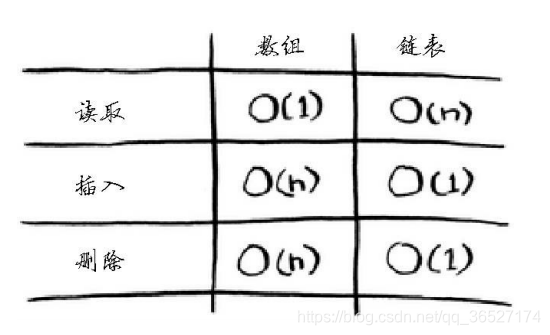
3.数组和链表相关操作的速度：

 

3.选择排序

    选择排序用大O表示法表示为：O（n^2）。

    工作原理：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。重复以上操作，直到全部待排序的数据元素的个数为零。

 

三、递归

1.递归函数的构成：基线条件和递归条件。递归条件指的是函数调用自己。而基数条件是函数不再调用自己的，从而避免无限循环。

2.数据结构：栈，入栈和出栈。先入后出。

3.调用栈：函数的调用，调用函数时计算机会分配一块内存来存储函数中的变量及调用其他函数的信息，先调用的函数和声明的变量会入栈压到栈底，释放的资源和变量时，出栈会先释放最后入栈的内存块。这就是调用栈。

4.递归也使用调用栈。

5.需要注意调用栈可能会很长，占用大量的内存。

比如：利用递归实现计算数组所有元素和。

<?php

$num=array(1,2,3,4);

function sum($n){

    if(count($n)>0){

        $tmp_value = array_shift($n);

        $s=sum($n)+$tmp_value;

    }else{

        $s=$n[0];

    }

    return $s;

}

echo sum($num);

     

四、快速排序

1.分而治之（D&C）

    快速排序其实是递归的。使用D&C算法解决问题分为两个步骤：

    1.找出基线条件，这种条件必须尽可能的简单；

    2.不断的将问题分解（或者缩小规模），知道符合基线条件。

 

    举个分而治之的例子：找出列表中最大的数字。    

<?php

$array = array(1,2,3,4,1,2,23,3);

function sum($arr){

        if(count($arr)>1){

                $tmp = array_shift($arr);

                if($tmp>$arr[0]){

                        $arr[0] = $tmp;

                }

                $arr = sum($arr);

        }

        return $arr[0];

}

ech