算法图解：总结篇

 

要计算两点的距离，可使用毕达哥拉斯公式。这种距离指出了两组数字之间的相似程度。

在实际工作中，经常使用余弦相似度（cosinesimilarity）。

OCR指的是光学字符识别（optical character recognition）,Google使用OCR来实现图书数字化。OCR是如何工作的呢?

一般而言，OCR算法提取线段、点和曲线等特征。

二分查找仅在数组有序时才管用。将新元素插入庞大数组并重新排序： 名为二叉查找树（binary search tree）的数据结构能将用新元素插入到数组的正确位置，这样就无需在插入后再排序。对于其中的每个节点，左子节点的值都比它小，而右子节点的值都比它大。

 

 

假设你要查找Maggie。为此，你首先检查根节点；Maggie排在David的后面，因此你往右边找。Maggie排在Manning前面，因此你往左边找。

在二叉查找树中查找节点时，平均运行时间为O(log n)，但在最糟的情况下所需时间为O(n)；

而在有序数组中查找时，即便是在最糟情况下所需的时间也只有O(logn)，因此你可能认为有序数组比二叉查找树更佳。

然而，二叉查找树的插入和删除操作的速度要快得多。

二叉查找树的缺点：不能随机访问；在二叉查找树处于平衡状态时，平均访问时间也为O(log n)。不平衡时性能更差。

有一些处于平衡状态的特殊二叉查找树，如红黑树。B树是一种特殊的二叉树，数据库常用它来存储数据。

请研究如下数据结构：B树，红黑树，堆，伸展树。

反向索引：搜索引擎的工作原理

先根据网页的内容创建一个散列表，这个散列表的键为单词，值为包含指定单词的页面。现在假设有用户搜索hi，在这种情况下，搜索引擎需要检查哪些页面包含hi。

一个散列表将单词映射到包含它的页面。这种数据结构被称为反向索引（inverted index），常用于创建搜索引擎。

傅里叶变换

傅里叶变换非常适合用于处理信号，可使用它来压缩音乐。为此，首先需要将音频文件分解为音符。傅里叶变换能够准确地指出各个音符对整个歌曲的贡献，让你能够将不重要的音符删除。这就是MP3格式的工作原理！

PG也是一种压缩格式/数字信号，也采用了同样的工作原理。傅里叶变换还被用来地震预测和DNA分析。

并行算法

在最佳情况下，排序算法的速度大致为O(n logn)。众所周知，对数组进行排序时，除非使用并行算法，否则运行时间不可能为O(n)！对数组进行排序时，快速排序的并行版本所需的时间为O(n)。

并行算法速度的提升并非线性的，即便你的笔记本电脑装备了两个而不是一个内核，算法的速度也不可能提高一倍，其中的原因有两个。

并行性管理开销。假设你要对一个包含1000个元素的数组进行排序，如何在两个内核之间分配这项任务呢？如果让每个内核对其中500个元素进行排序，再将两个排好序的数组合并成一个有序数组，那么合并也是需要时间的。

负载均衡。假设你需要完成10个任务，因此你给每个内核都分配5个任务。但分配给内核A的任务都很容易，10秒钟就完成了，而分配给内核B的任务都很难，1分钟才完成。这意味着有那么50秒，内核B在忙死忙活，而内核A却闲得很！你如何均匀地分配工作，让两个内核都一样忙呢？要改善性能和可扩展性，并行算法可能是不错的选择！

分布式算法 ：越来越流行的并行算法

MapReduce是一种流行的分布式算法，你可通过流行的开源工具ApacheHadoop来使用它。

分布式算法非常适合用于在短时间内完成海量工作，其中的MapReduce基于两个简单的理念：映射（map）函数和归并（reduce）函数。

映射函数接受一个数组，并对其中的每个元素执行同样的处理。映射是将一个数组转换为另一个数组。

arr1 = [1, 2, 3, 4, 5]
arr2 = map(lambda x: 2 * x, arr1)   # 结果：[2, 4, 6, 8, 10]

你有一个URL清单，需要下载每个URL指向的页面并将这些内容存储在数组arr2中。对于每个URL，处理起来都可能需要几秒钟。如果总共有1000个URL，可能耗时几小时！如果有100台计算机，而map能够自动将工作分配给这些计算机去完成就好了。这样就可同时下载100个页面，下载速度将快得多！这就是MapReduce中“映射”部分基本的理念。

归并函数的理念是将很多项归并为一项。归并是将一个数组转换为一个元素。

 arr1 = [1, 2, 3, 4, 5]
reduce(lambda x,y: x+y, arr1)     # 15

布隆过滤器和HyperLogLog

假设你在Google负责搜集网页，但只想搜集新出现的网页，因此需要判断网页是否搜集过。

给定一个元素，你需要判断它是否包含在这个集合中。为快速做出这种判断，可使用散列表。

例如，Google可能有一个庞大的散列表，其中的键是已搜集的网页。

散列表的平均查找时间为O(1)，即查找时间是固定的，非常好！

只是Google需要建立数万亿个网页的索引，因此这个散列表非常大，需要占用大量的存储空间。创造性的解决方案——布隆过滤器。

布隆过滤器是一种概率型数据结构，它提供的答案有可能不对，但很可能是正确的。

为判断网页以前是否已搜集，可不使用散列表，而使用布隆过滤器。

使用散列表时，答案绝对可靠，而使用布隆过滤器时，答案却是很可能是正确的。

 

布隆过滤器可能出现错报的情况，即Google可能指出“这个网站已搜集”，但实际上并没有搜集。

不可能出现漏报的情况，即如果布隆过滤器说“这个网站未搜集”，就肯定未搜集。

布隆过滤器的优点在于占用的存储空间很少。使用散列表时，必须存储Google搜集过的所有URL，但使用布隆过滤器时不用这样做。布隆过滤器非常适合用于不要求答案绝对准确的情况。

 HyperLogLog近似地计算集合中不同的元素数，它不能给出准确的答案，但也八九不离十，而占用的内存空间却少得多。面临海量数据且只要求答案八九不离十时，可考虑使用概率型算法！

散列函数

• 第一种：查找时间固定的，散列函数的结果是均匀分布的。散列函数接受一个字符串，并返回一个索引号。

假设你有一个键，需要将其相关联的值放到数组中。用散列函数来确定应将这个值放在数组的什么地方。当你想要知道指定键对应的值时，可再次执行散列函数，它将告诉你这个值存储在什么地方，需要的时间为O(1)。

• 第二种：另一种散列函数是安全散列算法（secure hash algorithm，SHA）函数。给定一个字符串，SHA返回其散列值【一个较短的字符串】

用于创建散列表的散列函数根据字符串生成数组索引，而SHA根据字符串生成另一个字符串。

对于每个不同的字符串，SHA生成的散列值都不同。

可使用SHA来判断两个文件是否相同，在比较超大型文件时很有用，可计算它们的SHA散列值，再对结果进行比较。散列值相同则为同一个文件。

SHA被广泛用于计算密码的散列值。这种散列算法是单向的。你可根据字符串计算出散列值。但你无法根据散列值推断出原始字符串。

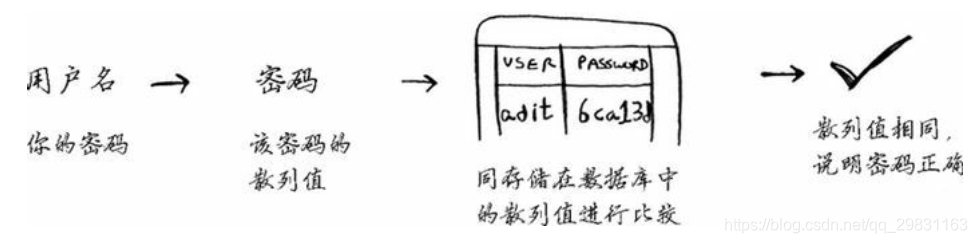
Google存储的并非密码，而是密码的SHA散列值！你输入密码时，Google计算其散列值，并将结果同其数据库中的散列值进行比较。你可将密码转换为散列值，但反过来不行。这意味着计算攻击者窃取了Gmail的SHA散列值，也无法据此推断出原始密码！

SHA实际上是一系列算法；如果你要使用SHA算法来计算密码的散列值，请使用SHA-2或SHA-3。当前，最安全的密码散列函数是bcrypt，但没有任何东西是万无一失的

局部敏感的散列算法

SHA还有一个重要特征，那就是局部不敏感的。假设你有一个字符串，并计算了其散列值。如果你修改其中的一个字符，再计算其散列值，结果将截然不同！

 

如果希望散列函数是局部敏感的，可使用Simhash。需要检查两项内容的相似程度时，Simhash很有用。

如果你对字符串做细微的修改，Simhash生成的散列值也只存在细微的差别。这让你能够通过比较散列值来判断两个字符串的相似程度，这很有用！

Google使用Simhash来判断网页是否已搜集。

老师可以使用Simhash来判断学生的论文是否是从网上抄的。

Diffie-Hellman密钥交换

Diffie-Hellman算法解决了一个古老的问题：如何对消息进行加密，以便只有收件人才能看懂呢？Diffie-Hellman算法解决了如下两个问题。

• 双方无需知道加密算法。他们不必会面协商要使用的加密算法。
• 要破解加密的消息比登天还难。

Diffie-Hellman使用两个密钥：公钥和私钥。Diffie-Hellman算法及其替代者RSA依然被广泛使用。

公钥就是公开的，可将其发布到网站上，通过电子邮件发送给朋友，或使用其他任何方式来发布。你不必将它藏着掖着。有人要向你发送消息时，他使用公钥对其进行加密。

加密后的消息只有使用私钥才能解密。只要只有你知道私钥，就只有你才能解密消息！

• 所有的图算法都可使用线性规划来实现。
• 大O表示法不考虑乘以、除以、加上或减去的数字。
• 数组的读取速度快，而插入速度慢；链表的读取速度慢，而插入速度快。当你要读取所有的元素时，链表的读取速度也不慢。
• 当你执行的插入操作比读取操作多时，使用链表更合适。另外，仅当你要随机访问元素时，链表的读取速度才慢。
• 经常要执行插入操作，正是链表擅长的。
• 数组让你能够随机访问——立即获取数组中间的元素，而使用链表无法这样做。要获取链表中间的元素，你必须从第一个元素开始，沿链接逐渐找到这个元素。
• 数组的插入速度很慢。另外，要使用二分查找算法来查找数组元素时，数组必须是有序的。因此每次插入元素后，你都必须对数组进行排序！
• 每个程序可使用的调用栈空间都有限，程序用完这些空间（终将如此）后，将因栈溢出而终止。
• 分查找的基线条件是数组只包含一个元素。如果要查找的值与这个元素相同，就找到了！否则，就说明它不在数组中。在二分查找的递归条件中，你把数组分成两半，将其中一半丢弃，并对另一半执行二分查找.