Leetcode 376. Wiggle Subsequence-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_36294507/article/details/112874634

这篇博客探讨了一种使用贪心策略解决最长摆动序列问题的方法。作者首先提出了两个关键命题：1) 最长的摆动序列必然包含数组的第一个元素；2) 以数组第一个元素为起点，选取单调区间极值能构成解。然后通过Python代码展示了如何从上升和下降两个方向分别计算最长摆动序列，并选择最长的那个作为结果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

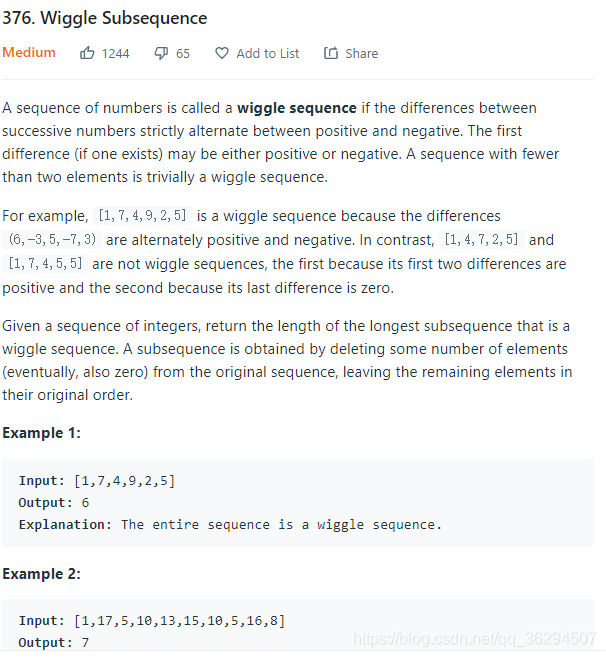
这道题是从dp的tag中找到的，但实际上可以使用贪心求解。

主要是明确两个真命题：

命题一、长度最长的符合要求的子序列中一定至少有一个子序列包含原数组第一个元素

证明：

使用反证法，假设长度最长的子序列均不包含第一个元素

1）当子序列从上升开始且第一个元素比原数组第一个元素大时，该子序列可使用原数组第一个元素替换其第一个元素，得到一个同长度的子序列解。

2）当子序列从上升开始且第一个元素比原数组第一个元素小时，该子序列应该加上原数组第一个元素，与长度最长冲突。

3)4）当子序列从下降开始同理

因此可证明命题一为真

命题二、以某个方向（增或减）从原数组第一个元素起始，由每一个单调区间上的极值组成的子序列一定是该方向上的一个解

证明：

由题意，每个单调区间最多只能选择一个元素，当我们选择单调区间极值时，子序列的长度是单调区间的个数，如果不选择极值，则可能少于这个数量。

class Solution(object):    def wiggleMaxLength(self, nums):        """        :type nums: List[int]        :rtype: int        """        if not nums:            return 0                res_up = 1        up = []        i=1        pre = nums[0]                direction = 1 #起始状态为上        while i<len(nums):            print(pre,direction,i)            if nums[i]>pre and direction==1:                res_up += 1                up.append(pre)                while i<len(nums) and nums[i]>=pre:                    pre = nums[i]                    i += 1                i -= 1                pre = nums[i]                direction = 0            elif nums[i]<pre and direction == 0:                res_up += 1                up.append(pre)                while i<len(nums) and nums[i]<= pre :                    pre = nums[i]                    i += 1                i -= 1                pre = nums[i]                direction = 1                        i += 1        up.append(pre)        print(up)                        res_down = 1        i=1        pre = nums[0]        direction = 0 #起始状态为下        down = []        while i<len(nums):            if nums[i]>pre and direction==1:                down.append(pre)                res_down += 1                while i<len(nums) and nums[i]>=pre:                    pre = nums[i]                    i += 1                i -= 1                pre = nums[i]                direction = 0            elif nums[i]<pre and direction == 0:                res_down += 1                down.append(pre)                while i<len(nums) and nums[i]<= pre :                    pre = nums[i]                    i += 1                i -= 1                pre = nums[i]                direction = 1            i += 1        down.append(pre)        print(down)        print(res_up,res_down)                    return max(res_up,res_down)