【leetcode】799. Champagne Tower

最新推荐文章于 2022-11-20 19:52:37 发布

原创最新推荐文章于 2022-11-20 19:52:37 发布 · 309 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode

本文介绍了一种利用动态规划解决LeetCode上经典香槟塔问题的方法。通过定义dp数组并设置状态转移方程，实现了高效计算倒入指定数量香槟后各杯子内香槟的体积。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述：

https://leetcode.com/problems/champagne-tower/

题目大意：

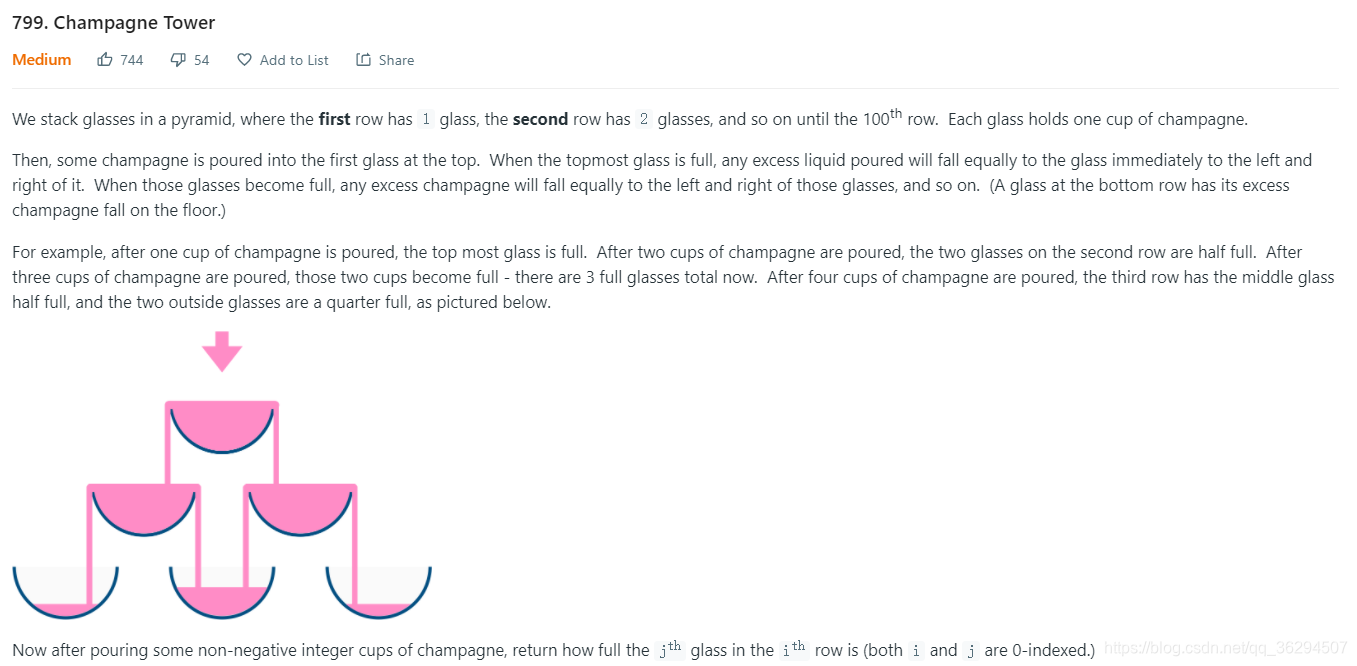
经典倒香槟场景，从由高脚杯叠成的金字塔最上一个杯子开始倒入poured数目的香槟，问倒完之后，第i行第j个杯子内有多少香槟。

解题思路：

这道题看到poured数据规模在e9，让人觉得需要寻找O（n）的解法，但实际上这道题的时间复杂度并不由poured的数量级决定。

在倒入一定体积香槟后，杯子金字塔中任意一个杯子内的香槟体积都是固定的，不涉及排列组合问题，因此基本不考虑dfs回溯，更多的可能是数学计算或者动态规划。

笔者使用动态规划对这道题进行求解。

在解题过程中，最重要的是动态规划数组元素的定义:

定义dp[i][j]为到完poured香槟后经过该杯子的香槟总体积（可以>1）

因此可得状态转移方程：

if dp[i][j]>1:
    dp[i+1][j] += (dp[i][j]-1)/2
    dp[i+1][j+1] += (dp[i][j]-1)/2

python代码为：

class Solution(object):
    def champagneTower(self, poured, query_row, query_glass):
        """
        :type poured: int
        :type query_row: int
        :type query_glass: int
        :rtype: float
        """
        if poured == 0:
            return 0
        dp = [[0.00000]*(query_row+1) for _ in range(query_row+1)]
        dp[0][0] = float(poured)
        for i in range(0,query_row):
            for j in range(i+1):
                if dp[i][j]>1:
                    dp[i+1][j] += (dp[i][j]-1)/2
                    dp[i+1][j+1] += (dp[i][j]-1)/2
        
        return min(1,dp[query_row][query_glass])

一个坑就是dp数组内的值要为float类型，输出为dp值与1取min