C++成长之路（4）——函数的递归调用

函数直接或间接地调用自身，称为递归调用

例如：计算n！

方法1（不使用递归）：

方法2（使用递归）：

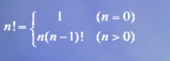
思路如下：

计算n！--完整代码 ：

#include <iostream>

using namespace std;

//计算n的阶乘
unsigned fac (unsigned n){
    unsigned f;
    if(n == 0)  f = 1;//规定：0！为1
    else
        f = fac(n - 1) * n;//递归调用，知道n为0
    return f;
}
int main()
{
    unsigned n;
    cout << "Enter a positive integer: ";
    cin >> n;
    unsigned y = fac(n);
    cout << n << "! = " << y <<endl;
    return 0;
}

程序分析：

1. 输入n = 3

2.调用fac（3） → f  = fac(2) * 3 → 调用fac(2) →  f  = fac(1) * 2 →  调用 fac(1) → f = fac(0) * 1 → fac(0) = 1

→ return f = 1, fac(1) = 1 → return f = 2, fac(2) = 2 →  return f = 6, fac(3) = 6

                                                                                                                                                                                   

运行结果：

思考题：

 一、求组合问题C（n,k）：

用递归法计算从n个人中选择k个人

 完整代码：

#include <iostream>

using namespace std;


int comm(int n, int k){//组合函数
    if(k > n)   return 0;
    else if(n == k || k == 0)   return 1;
    else return comm(n - 1,k) + comm(n - 1, k - 1);
}

int main()
{
    int n, k;
    cout << "Please enter two integers n and k:";
    cin >> n >> k;
    cout << "C(" << n <<"," << k << ")= " << comm(n, k) << endl;
    return 0;
}

运行结果：

二、汉诺塔问题

题目要求：

求解思路：

 代码如下：

#include <iostream>

using namespace std;

//把src针最上面的一个盘子，移动到dest指针
void move(char src, char dest){
    cout << src << " --> " << dest << endl;
}

//把n个盘子从src针移动到dest针，以medium针为中介
void hanoi(int n, char src, char medium, char dest){
    if(n == 1)
        move(src,dest);
    else{
        hanoi(n - 1, src, dest, medium);
        move(src, dest);
        hanoi(n - 1, medium, src, dest);
    }

}

int main()
{
    int m;
    cout << "Enter the number of diskes: ";
    cin >> m;
    cout << "the steps to moving " << m << "diskes: " << endl;
    hanoi(m, 'A', 'B', 'C');

    return 0;
}

 运行结果：

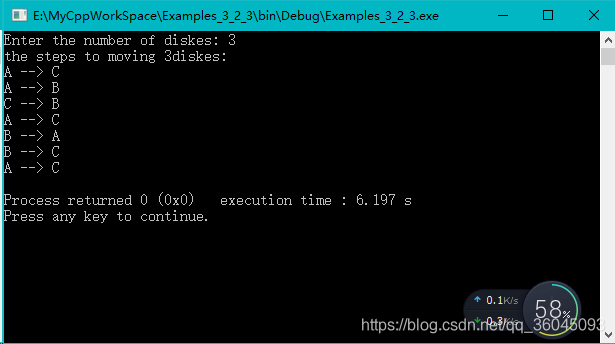
三、计算Fibonacci级数

题目：

 完整代码：

#include <iostream>

using namespace std;

int fib(int n){
    int f = 0;
    if(n ==1 || n == 2)
        f = 1;
    else
    f = fib(n - 1) + fib(n - 2);
    return f;
}
int main()
{
    int n;
    cout << "Enter a number:";
    cin >> n;
    cout << fib(n) << " is the " << n << "th Fibonacci number." << endl;
    return 0;
}

 运行结果：