数据结构——查找

最新推荐文章于 2023-08-08 09:56:29 发布

原创最新推荐文章于 2023-08-08 09:56:29 发布 · 471 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#查找 #数据结构 #二叉排序树 #索引

数据结构专栏收录该内容

7 篇文章

订阅专栏

本文深入讲解查找算法，包括顺序查找、折半查找、二叉排序树等，探讨各种算法的实现原理、性能分析及应用场景。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、定义

查找（Searching）就是根据给定的某个值，在查找表中确定一个其关键字等于给定值的数据元素（或记录）。

查找表（Search Table）是由同一类型的数据元素（或记录）构成的集合。
关键字（Key）是数据元素中某个数据项的值，又称为键值，用它可以标识一个数据元素。也可以标识一个记录的某个数据项（字段），称为关键码。
若此关键字可以唯一地标识一个记录，则称此关键字为主关键字（Primary Key）。
对于可以识别多个数据元素（或记录）的关键字，称为次关键字（Secondary Key）。

查找性能的评价指标——平均查找长度ASL
ASL：在查找的过程中，给定值K与关键字比较次数的期望值
$\sum_{i=1}^{n}{C_{i}*P_i}$
n表示查找表中记录的数量
$C_{i}$ 表示查找到第i条记录时，K与关键字的比较次数
$P_i$ 表示查找第i条记录的概率

1、静态查找表（Static Search Table）：只作查找操作的查找表

2、动态查找表（Dynamic Search Table）：在查找过程中同时插入查找表中不存在的数据元素或删除查找表中已经存在的某个数据元素。

二、顺序查找

1、定义

顺序查找（Sequential Search）又叫线性查找，是最基本的查找技术，它的查找过程是：从表中第一个（或最后一个）记录开始，逐个进行记录的关键字和给定值比较，若某个记录的关键字和给定值相等，则查找成功，找到所查的记录；如果直到最后一个记录，其关键字和给定值比较都不等时，则表中没有所查的记录，查找不成功。

2、顺序表查找算法

顺序查找

//顺序查找，a为数组，n为要查找的数组个数，key为要查找的关键字
int Sequential_Search(int *a, int n, int key){
	int i;
	for(i=1; i<=n; i++){
		if(a[i]==key)
			return i;
	}
	return 0;
}

顺序表查找优化
由于方法1中的顺序查找每次循环都需对i是否越界作判断，这里做一个优化，设置一个哨兵，不需要每次让i与n作比较。

//有哨兵顺序查找
int Sequential_Search2(int *a,int n,int key){
	int i;
	a[0]=key;//设置a[0]为关键字值，称为“哨兵”
	i=n;
	while(a[i] != key){
		i--;
	}
	return i;//返回0说明查找失败
}

顺序表查找效率：
查找成功时：
$\sum_{i=1}^{n}{(n-i+1)}*\frac{1}{n} = \frac{n+1}{2}$
查找失败时：
$A S L = n + 1$
平均情况：
$A S L = 3 (n + 1) / 4$

顺序表是最朴素的查找方法，对表的限制最少，适用于顺序存储结构和链式存储结构，但是时间性能最差O(n)

三、有序查找

1. 折半查找

折半查找（Binary Search）技术，又称二分查找。它的前提是线性表中的记录必须是关键码的有序（通常从小到大有序），线性表必须采用顺序存储。折半查找的基本思想是：在有序表中，取中间记录作为比较对象，若给定值与中间记录的关键字相等，则查找成功；若给定值小于中间记录的关键字，则在中间记录的左半区继续查找；若给定值大于中间记录的关键字，则在中间记录的右半区继续查找，不断重复上述过程，直到查找成功，或所有查找区域无记录，查找失败为止。

//折半查找
int Binary_Search(int *a, int n, int key){
	int low,high,mid;
	low = 1;
	high = n;
	while(low<=high){
		mid = (low+high)/2;
		if(key<a[mid])
			high=mid-1;
		else if(key>a[mid])
			low=mid+1;
		else 
			return mid;
	}
	return 0;
}

折半查找判定树：
折半查找的过程可以用二叉树来描述：把当前查找区间的中间位置上的结点作为根，左子表和右子表中的结点分别作为根结点的左子树和右子树，每个结点的值均大于其左子树上所有结点的值，小于其右子树上所有结点的值。由此得到的二叉树，称为二分查找树的判定树（Decision Tree）或比较树（Comprision Tree）。

例子：
在这里插入图片描述
详细可参考：https://blog.youkuaiyun.com/qq_28409193/article/details/50484638

折半查找：
1、折半查找要求必须是有序的顺序表;
2、折半查找效率高，时间复杂度为O( $log_{2}n$ );
3、折半查找判定树是分析查找性能的有效工具，查找每个结点所需的比较次数等于该结点在树上的层次数;
4、折半查找判定树是一棵理想平衡二叉树，树的高度为 $\lfloor\log_2 n\rfloor+1$ ;
5、无论查找是否成功，与关键字的最大比较次数都不会超过树的高度；

2. 插值查找

略

3. 斐波那契查找

略

四、线性索引查找

索引就是把一个关键字与它对应的记录相关联的过程。
索引按照结构可分为线性索引、树形索引和多级索引。
其中线性索引是将索引项集合组织为线性结构，也称为索引表。

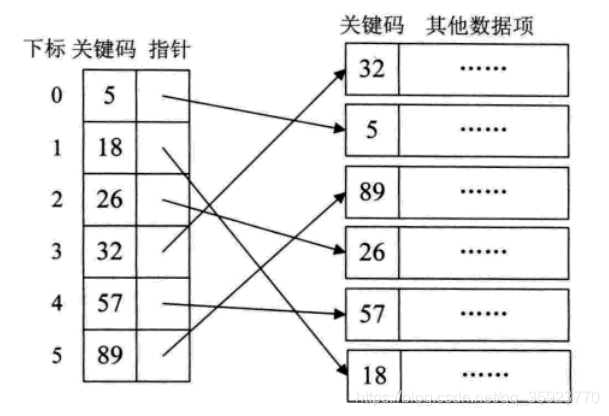
稠密索引
稠密索引是指在线性索引中，将数据集中的每个记录对应一个索引项，其中索引项一定是按照关键字代码有序的排列。
分块索引
分块有序就是把数据集的记录分成了若干块，并且这些块需要满足两个条件：
a、 块内无序，即每一块内的记录不要求有序。
b、 块间有序
对于分块有序的数据集，将每块对应一个索引项，这种索引方法称为分块索引。如图所示：

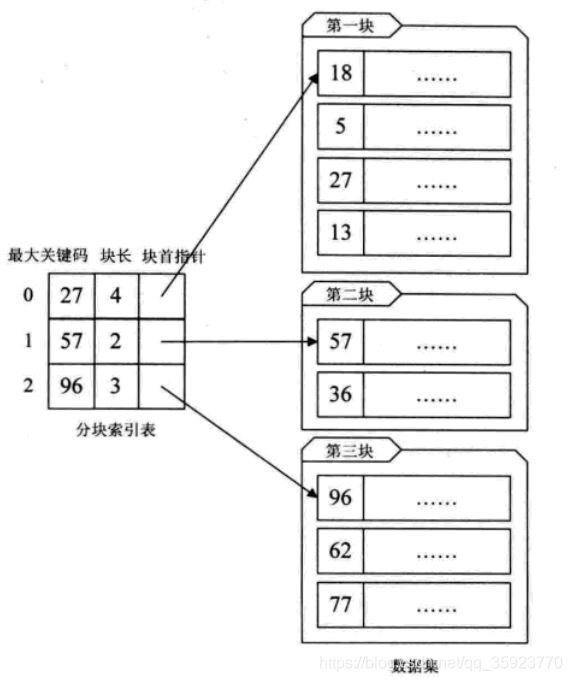
分块索引的索引项分为三个数据项：
a、最大关键码，存储每一块中的最大关键字，这样有利于是在他之后的下一块中的最小关键字也能比这一块最大的关键字要大
b、块长，存储块中记录个数，以便于循环时使用
c、块首指针，拥有指向数据元素的指针，便于开始对这一块中的记录进行遍历
分块索引查找：
1、在分块索引表中查找要查关键字所在的块。
2、根据块首指针找到相应的块，并在块中顺序查找关键码。
倒排索引

五、二叉排序树

二叉排序树（Binary Sort Tree），又称二叉查找树。它或者时一棵空树，或者具有下列性质：

若它的左子树不空，则左子树上所有节点的值均小于它的根结构的值；
若它的右子树不空，则右子树上所有节点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树。

1、二叉排序树查找操作

#define TRUE 1
#define FALSE 0

typedef int TElemType;
typedef struct BiTNode{
	TElemType data;
	struct BiTNode *lchild;
	struct BiTNode *rchild;
}BiTNode,*BiTree;

/*
递归查找二叉排序树T中是否存在key，
指针f指向T的双亲，初始值为NULL
若查找成功，则指针p指向该数据元素节点，并返回TRUE
否则指针p指向查找路径上访问的最后一个节点并返回FALSE
*/
//递归算法
int SearchBST(BiTree T, KeyType key, BiTree &f, BiTree &p){
	if(!T){//查找不成功
		p = f;
		return FALSE;
	}
	else if(key == T->data){//查找成功
		p = T;
		return TRUE;
	}
	else if(key < T->data)
		return SearchBST(T->lchild, key, T, p);
	else 
		return SearchBST(T->rchild, key, T, p);
}

//非递归算法
int BSTSearch(BiTree T, KeyType key,BiTree &f, BiTree &p){
	p = T;
	while(p){
		if(key < p->data){
			f = p;
			p = p->lchild;
		}
		else if(key > p->data){
			f = p;
			p = p->rchild;
		}
		else
			return TRUE;
	}
	return FALSE;
}

2、二叉排序树插入操作

/*当二叉排序树T中不存在关键字等于key的数据元素时，
插入key并返回TRUE*/
int InsertBST(BiTree &T, int key){
	BiTree p,s;
	if(!SearchBST(T, key, NULL, p)){//查找不成功
		s = new BiTNode;
		s->data = key;
		s->lchild = s->rchild = NULL;
		if(!p)
			T = s;
		else if(key < p->data)
			p->lchild = s;
		else
			p->rchild = s;

		return TRUE;
	}
	else
		return FALSE;//树中已有关键字相同的节点
}

3、二叉排序树删除操作

//从二叉排序树中删除节点p，并重接它的左右子树
int Delete(BiTree &p){
	BiTree q,s;
	if(p->rchild == NULL){//右子树为空,重接左子树
		q = p;
		p = p->lchild;
		free(q);
	}
	else if(p->lchild == NULL){//左子树为空，重接右子树
		q = p;
		p = p->rchild;
		free(q);
	}
	else{//左右子树均不为空
		q = p;
		s = p->lchild;
		while(s->rchild){//转左，找到待删结点的前驱
			q = s;
			s = s->rchild;
		}
		p->data = s->data;
		if(q != p)
			q->rchild = s->lchild;
		else
			q->lchild = s->lchild;
		free(s);
	}
	return TRUE;
	
}

int DeleteBST(BiTree &T, int key){
	if(!T)
		return FALSE;
	else{
		if(key == T->data)
			return Delete(T);
		else if(key < T->data)
			return DeleteBST(T->lchild, key);
		else
			return DeleteBST(T->rchild, key);
	}
}