Tarjan求LCA

我对Tarjan越来越崇拜了！
首先是最近公共祖先的概念(什么是最近公共祖先？)：

在一棵没有环的树上，每个节点肯定有其父亲节点和祖先节点，而最近公共祖先，就是两个节点在这棵树上深度最大的公共的祖先节点。

换句话说，就是两个点在这棵树上距离最近的公共祖先节点。

所以LCA主要是用来处理当两个点仅有唯一一条确定的最短路径时的路径。

有人可能会问：那他本身或者其父亲节点是否可以作为祖先节点呢？

答案是肯定的，很简单，按照人的亲戚观念来说，你的父亲也是你的祖先，而LCA还可以将自己视为祖先节点。

来看下面这张图

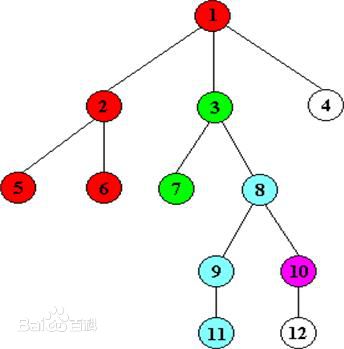
LCA(1,2)=1
LCA(2,4)=1

而对于求LCA的问题，有三种方法
1：倍增求LCA
2：DFS序+RMQ
3：Tarjan

前两种都使用了倍增的思想，而且是在线算法！

Tarjan是一种离线算法，复杂度O（n+m）n为点的数量，m查询的数量。
对于查询比较少的问题，Tarjan算法比较有优势。


图1为Tarjan算法（不使用快读）
图2为倍增算法（使用快读）

可以很明显的看出Tarjan的优势.

下面是具体实现

总思路就是每进入一个节点u的深搜，就把整个树的一部分看作以节点u为根节点的小树，再搜索其他的节点。每搜索完一个点后，如果该点和另一个已搜索完点为需要查询LCA的点，则这两点的LCA为另一个点的现在的祖先。

1.先建立两个链表，一个为树的各条边，另一个是需要查询最近公共祖先的两节点。

2.建好后，从根节点开始进行一遍深搜。

3.先把该节点u的father设为他自己（也就是只看大树的一部分，把那一部分看作是一棵树），搜索与此节点相连的所有点v，如果点v没被搜索过，则进入点v的深搜，深搜完后把点v的father设为点u。

4.深搜完一点u后，开始判断节点u与另一节点v是否满足求LCA的条件，满足则将结果存入数组中。

5.搜索完所有点，自动退出初始的第一个深搜，输出结果。

如上图，根据实现算法可以看出，只有当某一棵子树全部遍历处理完成后，才将该子树的根节点标记为有颜色（初始化是白色），假设程序按上面的树形结构进行遍历，首先从节点1开始，然后递归处理根为2的子树，当子树2处理完毕后，节点2， 5， 6均为红色；接着要回溯处理3子树，首先被染色的是节点7（因为节点7作为叶子不用深搜，直接处理），接着节点7就会查看所有询问(7, x)的节点对，假如存在(7, 5)，因为节点5已经被染黑，所以就可以断定(7, 5)的最近公共祖先就是find(5)，即节点1（因为2子树处理完毕后，子树2和节点1返回了合并后的树的根1，此时树根的祖先的值就是1）。
luogu模板题
实现代码

#include <cstdio>
#include <iostream>
using namespace std;
const int maxm=501000;
struct node{
    int net;
    int to;
    int lca;
};
bool vis[maxm];
int fat[maxm];
node edge[2][2*maxm];
int cnt[2],head[2][maxm];
void add(int id,int x,int y)
{
    edge[id][++cnt[id]].to=y;
    edge[id][cnt[id]].net=head[id][x];
    head[id][x]=cnt[id];
}
int find(int x)
{
    if(fat[x]==x) return x;
    else return fat[x]=find(fat[x]);
}
void dfs(int x)
{
    vis[x]=1;
    fat[x]=x;//以x为根节点的子树

    for(int K=head[0][x];K;K=edge[0][K].net)
    {
        int p=edge[0][K].to;
        if(vis[p]) continue;
        dfs(p);
        fat[p]=x;
    }

    for(int i=head[1][x];i;i=edge[1][i].net)
    {
        int p=edge[1][i].to;
        if(!vis[p]||edge[1][i].lca) continue;
        edge[1][i].lca=find(p);//找LCA
        if(i%2)
         edge[1][i+1].lca=edge[1][i].lca;
        else
         edge[1][i-1].lca=edge[1][i].lca;
    }
}
int main()
{
    int n,m,p;
    scanf("%d%d%d",&n,&m,&p);
    for(int i=1;i<n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add(0,x,y);
        add(0,y,x);
    }
    for(int i=1;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add(1,x,y),add(1,y,x);//一定要存双向的，因为你不知道那个节点先访问到
    }

    dfs(p);//根节点

    for(int i=1;i<=m;i++)
     printf("%d\n",edge[1][2*i].lca);
}