目录
1. 两点分布
-
定义: 实验的结果只有两种情况,即随机变量只有两个值,则称随机变量ξ服从两点分布。
-
分布律
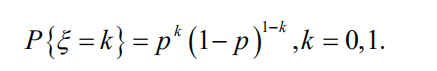
-p:表示实验成功的概率。 -
分布函数
-
概率密度函数
-
期望: E(ξ) = p
-
方差: D(ξ) = p(1-p)
2. 二项分布/伯努利分布 【X~B(n, p)】
-
定义: n个相互独立的两点分布的组合,具体分布律如下:
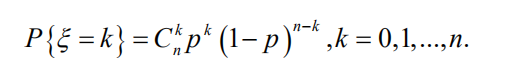
(ⅰ)当n为1时,即为两点分布。
(ⅱ)当n趋于无穷大时,即为泊松分布。 -
分布函数:
-
概率密度函数:
-
期望: E(ξ) = np
-
方差: D(ξ) = np(1-p)
✈二项分布最大值问题。
3. 泊松分布【ξ ~ P(λ)】
-
定义:
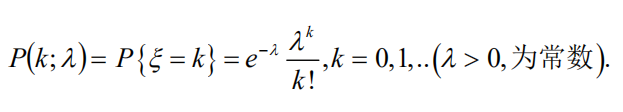
-λ:(一次实验中,实验成功的概率pn )× (总的试验次数n) -
分布函数
-
概率密度函数
-
期望: E(ξ) = λ
-
方差: D(ξ) = λ
泊松定理
4. 几何分布【ξ ~ Ge§】
- 分布函数
- 概率密度函数
- 期望: E(ξ) = 1/p
- 方差: D(ξ) = (1-p) / p2
几何分布的无记忆性
5. 超几何分布 【ξ ~ H(n, M , N)】
- 分布函数
- 概率密度函数
- 期望
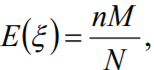
- 方差
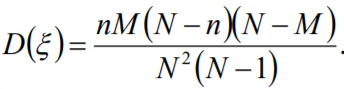
超几何分布的二项分布近似:
当n<<N时,
6. 负二项分布
期望
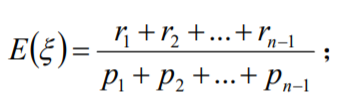
方差
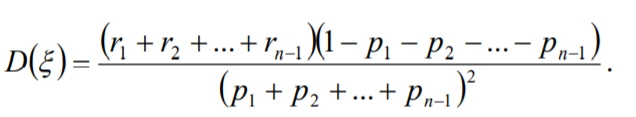








 本文系统地介绍了六种常见的离散型随机变量分布,包括两点分布、二项分布、泊松分布、几何分布、超几何分布及负二项分布。详细探讨了每种分布的定义、分布律、分布函数、概率密度函数、期望与方差等核心概念,为理解随机现象提供坚实的数学基础。
本文系统地介绍了六种常见的离散型随机变量分布,包括两点分布、二项分布、泊松分布、几何分布、超几何分布及负二项分布。详细探讨了每种分布的定义、分布律、分布函数、概率密度函数、期望与方差等核心概念,为理解随机现象提供坚实的数学基础。
















 3885
3885

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








