POJ P1958 Strange Towers of Hanoi

目录：

---

题目：

传送门

---

分析

首先我们定义只有三根柱子时有n个盘的话移动次数是$dn$，然后$dn=dn−1∗2+1$
定义有四根柱子时有n个盘移动次数为$fn$
之后我们看四根柱子

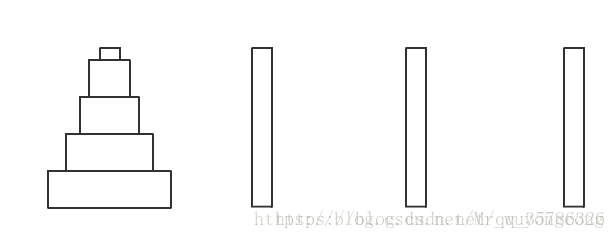
我们可以将这个塔任意分割成两部分，上面有k个，一个有n个

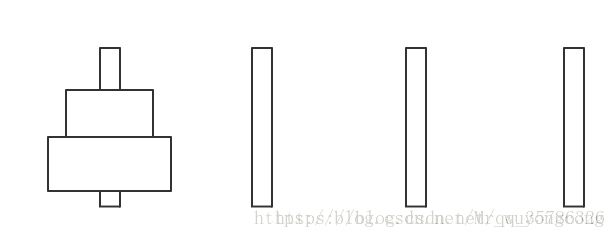
之后我们开始移动上面的

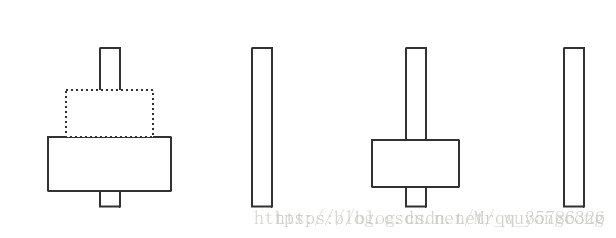
次数$fk$
然后我们移动下面的到第4个柱子

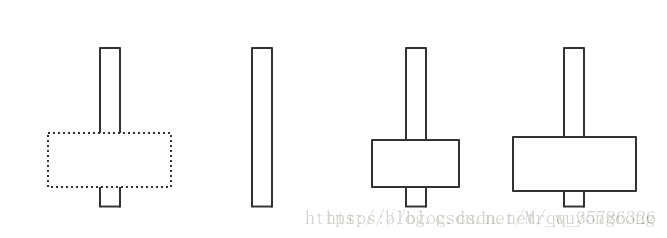
这时无论如何也不可以到达第3根柱子于是我们可以看作只有3个盘，于是次数$dn−k$
最后我们在将小盘移过去

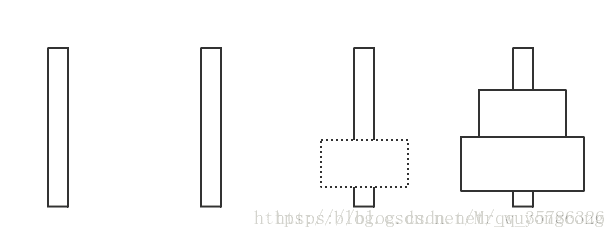
这时消耗$fk$
于是总代价为$fk∗2+dn−k$
之后我们枚举取最优的答案就好了。

---

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#define LL long long
using namespace std;
inline LL read() {
    LL d=0,f=1;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){d=d*10+s-'0';s=getchar();}
    return d*f;
}
int d[15],ans[15];
int min(int x,int y)
{
    return x<y?x:y;
}
int main()
{
    for(int i=1;i<=12;i++) d[i]=1+2*d[i-1];
    for(int i=1;i<15;i++) ans[i]=99999999;
    ans[1]=1;
    printf("1\n");
    for(int j=2;j<=12;j++)
    {
        for(int i=1;i<j;i++)
          ans[j]=min(2*ans[i]+d[j-i],ans[j]);
        printf("%d\n",ans[j]);
    }
    return 0;
}