数据结构--线性表3

前言

每天要学习的太多，今天花大量时间敲完静态链表的代码，发现后面还有循环链表，双向链表，这样学习效率太低。所以后面不打算把伪码重新实现一遍，只记录学习的要点等。

静态链表

通过物理的线性结构实现逻辑的链式存储，下标由0开始，及S[0]为第一个数据。

typedef struct
{
	ElemTpye data;
	int cur;  /* 游标(Cursor) ，为0时表示无指向 */
} Component, StaticLinkList[MAXSIZE];

静态链表的实现，最大的问题是区分那些空间是已经使用的还是没有使用的。
刚开始异想天开，自己这样实现的:
将游标利用起来，cur=-1代表空间是空闲的，cur>=0代表指向下一个使用的空间。当malloc时候，就将对应的下标修改为>0的，free时候，就将下标修改为-1，这样也能实现，但每次都遍历一遍 时间复杂度为N。

//通过遍历的方式返回该表中空闲的空间下标
int  SearchFree(StaticLinkList L)
{
	int i=1;
	while (i < MAXSIZE)
	{
		if (L[i].cur == -1)
			return i;
		i++;
	}
	return ERROR;
}

其实正确的思路是这样：
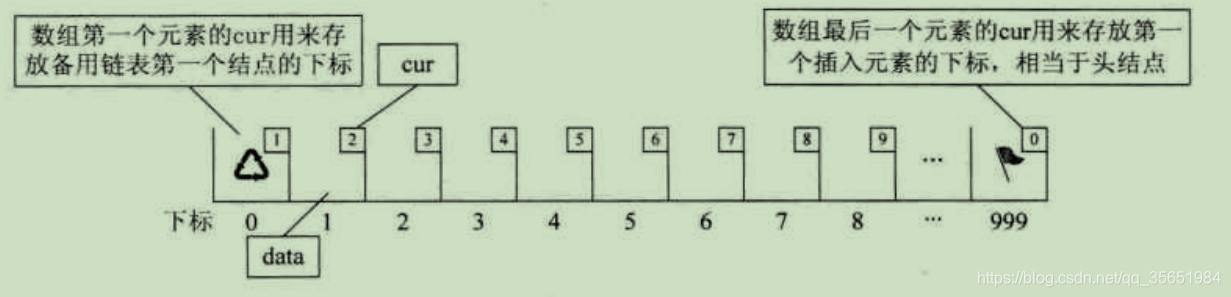
让数组的第一个元素cur存放第一个备用元素（未被占用的元素）下标，而数组的最后一个元素cur存放第一个有值的元素下标，相当于头结点作用。每当进行插入时候便返回备用链表的第一个节点，进行删除时候便将删除的节点连接到备用链表的第一个节点。

//从备用链表获得一个空闲空间下标
int Malloc_SSL(StaticLinkList space) 
{ 
	int i = space[0].cur;           		/* 当前数组第一个元素的cur存的值 */
	                                		/* 就是要返回的第一个备用空闲的下标 */
	if (space[0]. cur)         
	    space[0]. cur = space[i].cur;       /* 由于要拿出一个分量来使用了， */
	                                        /* 所以我们就得把它的下一个 */
	                                        /* 分量用来做备用 */
	return i;
}


/*  将下标为k的空闲结点回收到备用链表 */
void Free_SSL(StaticLinkList space, int k) 
{  
    space[k].cur = space[0].cur;    /* 把第一个元素的cur值赋给要删除的分量cur */
    space[0].cur = k;               /* 把要删除的分量下标赋值给第一个元素的cur */
}

删除一个元素,先循环到当前的i位置，将i-1游标指向i+1游标，并将i添加到备用链表

/*  删除在L中第i个数据元素   */
Status ListDelete(StaticLinkList L, int i)   
{ 
    int j, k;   
    if (i < 1 || i > ListLength(L))   
        return ERROR;   
    k = MAXSIZE - 1;   
    for (j = 1; j <= i - 1; j++)   
        k = L[k].cur;   
    j = L[k].cur;   
    L[k].cur = L[j].cur;   
    Free_SSL(L, j);   
    return OK;   
} 

增加同理

/*  在L中第i个元素之前插入新的数据元素e   */
Status ListInsert(StaticLinkList L, int i, ElemType e)   
{  
    int j, k, l;   
    k = MAXSIZE - 1;   /* 注意k首先是最后一个元素的下标 */
    if (i < 1 || i > ListLength(L) + 1)   
        return ERROR;   
    j = Malloc_SSL(L);   /* 获得空闲分量的下标 */
    if (j)   
    {   
		L[j].data = e;   /* 将数据赋值给此分量的data */
		for(l = 1; l <= i - 1; l++)   /* 找到第i个元素之前的位置 */
		   k = L[k].cur;           
		L[j].cur = L[k].cur;    /* 把第i个元素之前的cur赋值给新元素的cur */
		L[k].cur = j;           /* 把新元素的下标赋值给第i个元素之前元素的ur */
		return OK;   
    }   
    return ERROR;   
}

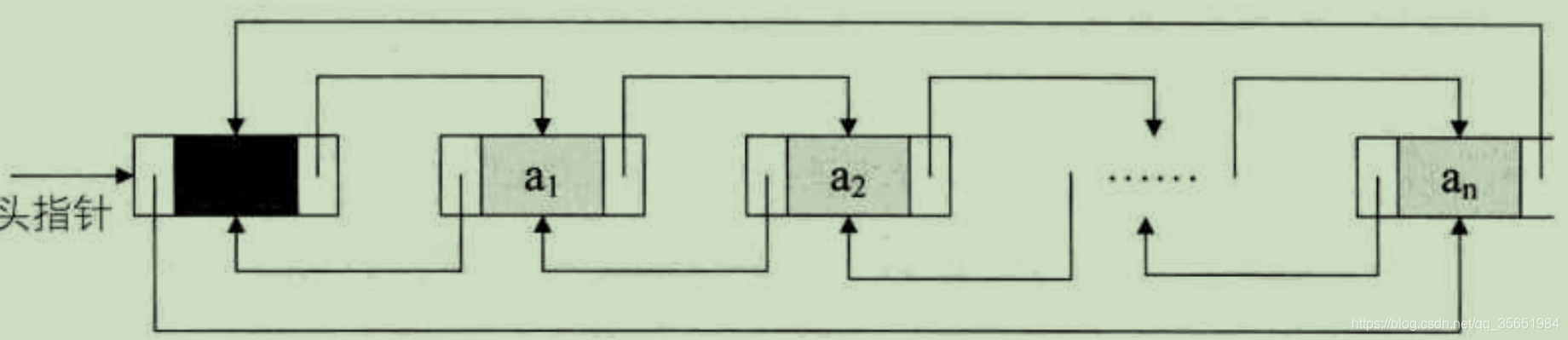
循环链表

表中的最后一个节点指针指向指向头节点，整个链表形成一个环
与线性链表差别在：判断是否循环完成的条件，由p->next是否为空变为是否等于头指针。

双向链表

双向链表为空：p->next=p->prior等于头指针

typedef struct
{
	ElemTpye data;
	struct DuLNode *prior;
	struct DuLNode *next;
	
} DuLNode, StaticLinkList[MAXSIZE];

插入

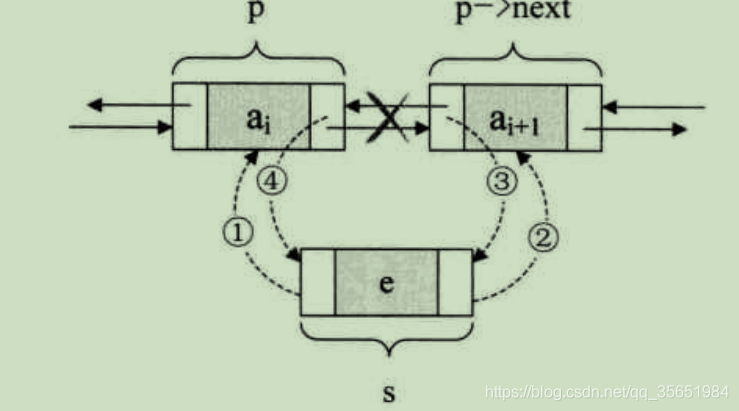
先填充待插入元素的前驱和后继，再由后到前释放原指针

s->prior =p
s->next =p->next
p->next ->prior=s;
p->next=s

删除

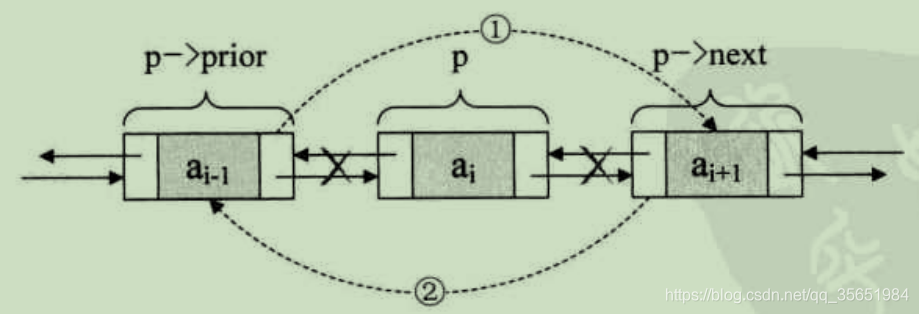
双向链表满足：
p->next->prior=p->prior->next