Distilling the Knowledge in a Neural Network

知识蒸馏：很多时候大模型效果好而小模型效果不行不一定是小模型容量不够，而可能是直接去拟合训练集太困难，因此诞生了知识蒸馏方法，主要思想是用一个大模型去学训练集，然后小模型去学大模型预测的结果，就容易多了。

以前的方法怎么做的？博客

简单来说是让小模型去学习大模型预测的softmax结果

本文呢？不去学大模型预测的softmax结果，而是学分类层输出的结果

首先是本人结合论文总结的几个观点，不一定对：

• (0.1,0.3,0.2,0.4)这种soft的标签，比(0,0,0,1)这种hard标签更好学一些，包含的信息更丰富，学到的效果更好。因为hard表示模型不可能为前三类，而soft则是给了一个较低的概率，在有noise时前者泛化性更强
• 分类层输出的结果又比(0.1,0.3,0.2,0.4)这种softmax输出结果更好学，效果更好。因为分类层的输出经过了BN，是零均值的，正负都有，但softmax直接全都归一化到零一之间，缺乏对称性，那些负的结果没有很好的发挥作用。这一点也是为什么目前设计的激活函数都想设计成零均值的(relu不是，因此大家想改进)

作者咋做的？

对softmax进行改进：

其中$z$是分类层结果经过BN的输出，$q$是改进的softmax的输出，也就是属于某一类的概率，其中$q_i$就是输入属于第i类的概率。而$T$是Temperature参数，设置为1时上式就是softmax函数。

经过改进的softmax的输出$q$，就可以计算出模型的交叉熵损失CE，记为C。

首先推导以下普通交叉熵损失和交叉熵损失对于$z_i$的偏导怎么算：

而无论是hard的标签，还是soft标签，都有$\sum y_i=1$，因此，上述偏导最终结果$=s_i-y_i$

那么，改进的带Temperature的softmax和普通softmax差别在哪呢？就是上图中带两个星号的波浪线处，计算偏导时各项会多出一个$1/T$将softmax表达式替换为：

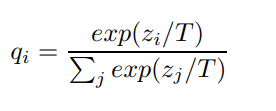
并且使用大模型预测的soft标签作为GT监督小模型的改进softmax网络，最终，也就可以得到改进的带Temperature的softmax对于的偏导为：

注意图片推导里的$s$就是改进softmax的$q$，而图片里的GT为$y$，对于改进softmax的soft标签$p$，且soft标签有$\sum p_i=1$

上式即为小模型在soft标签下的偏导

继续地，作者指出，在T很大时有：

这是因为在$x$接近0时，根据泰勒展开有：$e^x$可以近似为$1+x$，这才有上式的结果

而由于分类层会带一个BN，然后送给softmax，因此$z$和$v$都是零均值的，而$z$和$v$都是$N$维的向量，即分类层FC的神经元个数（N是类别数），不是无穷的，因此$\sum z_j/T$近似为0（只有无穷个0相加结果才不可以认为是0，有限个极限为0的项的和仍是0），另一项同理。

于是上式可以进一步简化为：

括号前是常数，可以不管，所以上式等于在说：相当于是在直接优化小模型分类层经过BN的输出和大模型保持一致，这比优化softmax输出可直接多了，因为避免了对称性的滤除(softmax直接将负的输出全部拉正到零一之间了)。

当然，上述推导的前提是$T$比较大，$T$比较小的时候和softmax差不多($T>=1$)

模型训练方式(作者的训练方式)：

• 大模型在训练集上训练模型
• 在较大T的情况下训练小模型
  • 大模型针对每个样本进行预测，得到改进softmax输出，当作GT给小模型学习
  • 小模型在改进softmax的情况下去学吧所谓的soft的GT吧
• 在T=1的情况下继续训，即正常的softmax
  • 这时可以使用大模型的正常的softmax输出作为GT给小模型学
  • 也可以直接用训练集的hard标签，比如用个3%的数据（而完全不用就是无监督了）

最终效果在多种任务下都是不错的。

个人收获：

• 可以蒸馏大模型
• 也可以用作知识迁移，这些就可以做域适应了

文中的几个可以和其他问题串起来的点：

• FC经过BN的负的输出不能直接舍弃，因为其实包含了大量信息，那么relu该如何自处？

负的部分直接置零损失了大量信息，并且输出不是零均值，不对称

于是可以看到relu的一些改进：

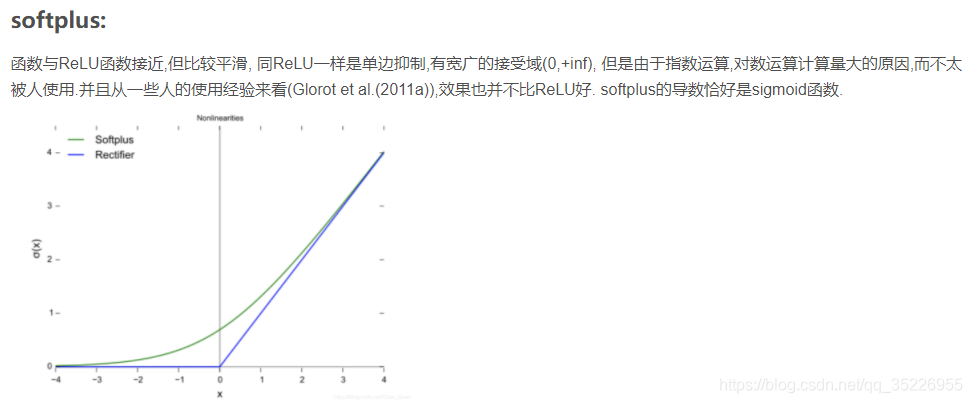
貌似在规避将负的输出直接置零

貌似也在规避这一点，同时规避非零均值和不对称问题

感觉有诸多相通之处

• T参数太大太小军不好，所以取中庸之道吧
• 带T的改进softmax时如何比普通softmax work的？

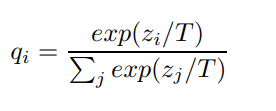
可以得到$1/q_i=e^{(z_1-z_i)/T}+e^{(z_2-z_i)/T}+...+e^{(z_{i-1}-z_i)/T}+1e^{(z_{i+1}-z_i)/T}+...+e^{(z_n-z_i)/T}$

现在各种论文中常用的一般是T<1的情况，比如0.1，相较于普通的softmax，T减小使得$q_i$减小
而交叉熵损失$L=-\sum y_{i}log{q}_i$，这使得L增大，而网络的目标是使得minL，于是训练网络输出的z会更有利于L减小，反复在L增大和L减小的过程中博弈，最终模型越来越强，鉴别性越来越高

而本文则是T>1的情况，与上述刚好相反，使得L减小。最终在T趋向于无穷时，q趋向于$(1/n,1/n,...,1/n{)}^T$，其实就是瞎猜了，各打五十大板。而交叉熵损失$L=-\sum y_{i}log{q}_i$，在hard标签下，损失就是$-log(1/n)$,这时L减小使得模型鉴别性降低，这也是为何作者会加一个T减小到1的softmax交叉熵的原因，因为可以增强鉴别性；而如果是softmax，在T增大时就可以实现作者那种优化分类层的BN输出，比优化softmax输出更直接。