Java：float/double取值范围与精度、BigDecimal

0、基本数据类型

1、浮点数的表示

• 在同等位数的情况下，浮点数可表示的数值范围比整数的大；
• 浮点数无法精确表示其数值范围内的所有数值，只能精确表示可用科学计数法m*2^e表示的数值而已;（如0.5的科学计数法是2^-1，则可被精确存储；而0.2则无法被精确存储）
• 浮点数不仅可表示有限的实数，还可以表示有限的整数。

1.1 浮点数结构

要说清楚Java浮点数的取值范围与其精度，必须先了解浮点数的表示方法，浮点数的结构组成，之所以会有这种所谓的结构，是因为机器只认识0和1，你想表示小数，你要机器认识小数点这个东西，必须采用某种方法，比如，简单点的，float四个字节，前两个字节表示整数位，后两个字节表示小数位（这就是一种规则标准），这样就组成一个浮点数。而Java中浮点数采用的是IEEE 754标准。

1.2 IEEE 754

这里就不细说什么是IEEE 754了，就直接讲具体内容，有兴趣的可以自己百度。

1.3 float

1.3.1 第一种表示方法

4 bytes	实数符号位：31	指数符号位：30，指数位：29—23	有效数位：22—0

• 符号位1表示正，0表示负，包括了实数符号位和指数符号位
• 指数位 = 指数符号位 + 指数位（严格上不太对，还是看第二种表示方法吧）
• 剩下的23位表示小数部分，这里23位表示了24位的数字，因为有一个默认的前导1(只有二进制才有这个特性)，即有效位数为24位，其中一位是实数符号位，

1.3.2 第二种表示方法

符号位(S):1bit	指数位(E):8bit	尾数位(M): 23bit

一个float4字节32位，分为三部分：符号位，指数位，尾数位。

• 符号位(S)：最高位（31位）为符号位，表示整个浮点数的正负，0为正，1为负；
• 指数位(E)：23-30位，共8位为指数位，这里指数的底数规定为2（取值范围：0~255），这一部分的最终结果格式为： 2^(E−127)，即范围-127~128。另外，标准中还规定了，当指数位8位全0或全1的时候，浮点数为非正规形式（这个时候尾数不一样了），所以指数位真正范围为：-126~127。其用移码表示
• 尾数位(M)，即小数部分：0-22位共23位为尾数位，表示小数部分的尾数，即形式为1.M或0.M，至于什么时候是1，什么时候是0，则由指数和尾数共同决定。 小数部分最高有效位是1的数被称为正规（规格化）形式，小数部分最高有效位是0的数被称为非正规（非规格化）形式，其他情况是特殊值。 最终float的值 = (−1)^S∗(2^E−127)∗(1.M)，其用原码表示。Java中float的取值范围的具体形式如下：
  

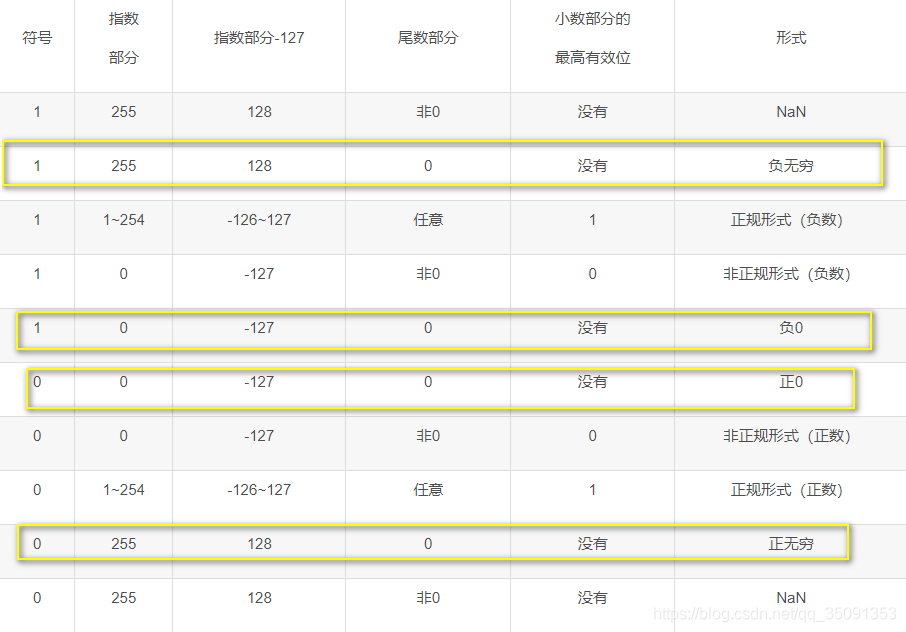
根据上表可知，float的取值范围：负无穷 —— −2¹²⁸ ~~ −2⁻¹⁴⁹ —— 0 —— 2⁻¹⁴⁹ ~~ 2¹²⁸ —— 正无穷：

• （1）上面的“——”表示中间不能取值，例如负无穷到−2¹²⁸中间的值是取不到的（事实上128也是取不到的，只是接近近似值），同时，这也并不是意味着，“~”表示的任意值都能取到，要注意，浮点数都是有精度的，并不能表示绝对值任意小的值。另外，Java中无穷大表示为：

Float.POSITIVE_INFINITY或Double.POSITIVE_INFINITY	//表示正无穷大
Float.NEGATIVE_INFINITY或Double.NEGATIVE_INFINITY	//负无穷大
//  打印的结果：+/-Infinity

// 要加(float)强制转换，否则编译提示出错
float f1 = (float)Math.pow(2,128);		//指数>=128的，打印结果：Infinity
float f2 = (float)Math.pow(2,127);//1.7014118E38
System.out.println(Float.MAX_VALUE);//3.4028235E38

• （2）-149的由来：看上面理论应该是150（指数全0，则指数值 = 0 -127=-127，这个时候尾数取最小，即2⁻²³，则-127-23 = -150），可不知道为什么是149，我查到的资料是说，全0，全1为特殊值，不作为范围内的值，上面的float的最大最小值Float.MAX_VALUE都是接近2¹²⁸）。故值 = (−1)^S∗(2⁻¹²⁶)∗(2⁻²³) = +/-2⁻¹⁴⁹

float f3 = (float) Math.pow(2,-149)//1.4E-45，小于-149，结果则为0.0
Float.MIN_VALUE //1.4E-45

• （3）float的尾数：23位，其范围为：0~2²³，而2²³=8388608=10^6.92，所以float的精度为6~7位，能保证6位为绝对精确，7位一般也是正确的，8位就不一定了（但不是说8位就绝对不对了），注意这里的6~7位是有效小数位（大的数你先需要转换成小数的指数形式，例如：8317637.5，其有效小数位：8.3176375E6，七位），而有效位（从第一个不为0的开始数）是7~8位，是包括整数位的，像8317637.5，你不转换，则要从有效位的角度来看，有8位有效位。

System.out.println((float)Math.pow(10,6.92));//注意加float强制转换
//打印结果8317637.5，float只保证7~8位有效位，其余位数舍入

不理解的话，可以再这样想：23位，二进制0101……0101，尾数表示小数位，最小为0000……0001（22个0，最后一个1），即2⁻²³=1.1920929E-7，这是float的最小单元（大概是0.0000001192大小，你想表示比这更小的，比如0.00000001，不可能啊），这是一个7位小数位小数，最小就是这么小，比这个更小的，计算机就无能为力了，比这个更大的，每次通过加这么一个最小单元，直到相等或接近（两个相差一个最小单元的数，它们之间的数也是不能表示的，所以有的7位也是不能精确的，因为最小不是0.0000001，而是比这个稍大）。

• Java中double类型的格式基本遵循IEEE 754标准。尽管数学意义上的小数是连续的，但double仅仅能表示其中的一些离散点，把这些离散点组成的集合记为S，S的大小还是有限的。如果要保存的小数P刚好在集合S内，那么double类型就能精确的表示P；否则double类型只能从集合S中找一个与P最近的离散点P'代替P。以上表述对于float也成立。IEEE 754中float和double的表示策略完全相同，区别仅仅体现在各个字段（指数字段、小数字段）的bit数量不同，也就是说，float和double都是不精确的。

1.4 double

符号位(S):1bit	指数位(E):11bit	尾数位(M): 52bit

• double这里就类似float，只是double的长度更大，所以范围就更大，但规则是一样的。double的值 = (−1)^S∗(2^E−1023)∗(1.M)

• double的取值同float：负无穷 —— −2¹⁰²⁴ ~~~ −2⁻¹⁰⁷⁴ —— 0 —— 2⁻¹⁰⁷⁴ ~~2¹⁰²⁴—— 正无穷，其中 1074 =| (-1022) - (52)|

• 另外，注意表格中，还有NaN，即表示非数值，例如：

System.out.println(0.0/0.0);  //打印结果：NaN。注意不能是 0/0
//NaN表示计算错误，具体出现情况，可以参考表中
//Float.NaN或 Double.NaN 也能直接表示NaN，NaN与其他数计算结果均为NaN，除了
Math.pow(Float.NaN,0);//结果为1.0
//另外NaN == NaN; false

• 计算方