如何通俗易懂地理解大模型参数?

大型语言模型 (LLM) 的大小是通过参数数量来衡量的。举几个典型例子，GPT-3 有 1750 亿个参数，1750亿也可称为175B（1B = 10亿），Meta最新开源的Llama3 参数数量在 80 亿到 700 亿之间，智谱公司最新开源的GLM4-9B参数为90亿。

这就有一个问题，什么叫做参数？

LLM 被称之为基于深度神经网络的大模型，为了了解这个非常复杂的模型，我们关注一个最简单并且与我们日常生活息息相关的的例子。

假设你是一名房地产经纪人，正在估算房屋的价值。你最近看到很多房子被卖出，并得出了一个简单的经验法则，即房子的价格约为每间房间 75,000 英镑。你可以用公式来表示：

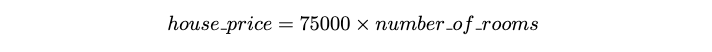
从上面这公式可以看出，输入只有一个房间数量，75000称之为参数。然后再来看一个复杂一点的例子，我假设房子价格依赖于房间数量与修建年份，用公式表示为：

从上面这公式可以看出，输入有二个分别是房间数量和修建年份，其中50000、-1000称之为参数。

上面两个公式，我们可以理解成最简单意义上的模型。不过在实际情况中，会发现这两个模型都不是最准确的，房子价格受到周围多种因素影响，实际中可以列出一个更长的输入列表来影响房价，比如最近的学校有多远以及厕所的数量。通过往模型添加越来越多的输入和参数，并调整参数的值，模型可能会得到越来越好的房价估计。假设确定了7个你认为对房价最重要的输入。为了方便理解，可以画成图表。

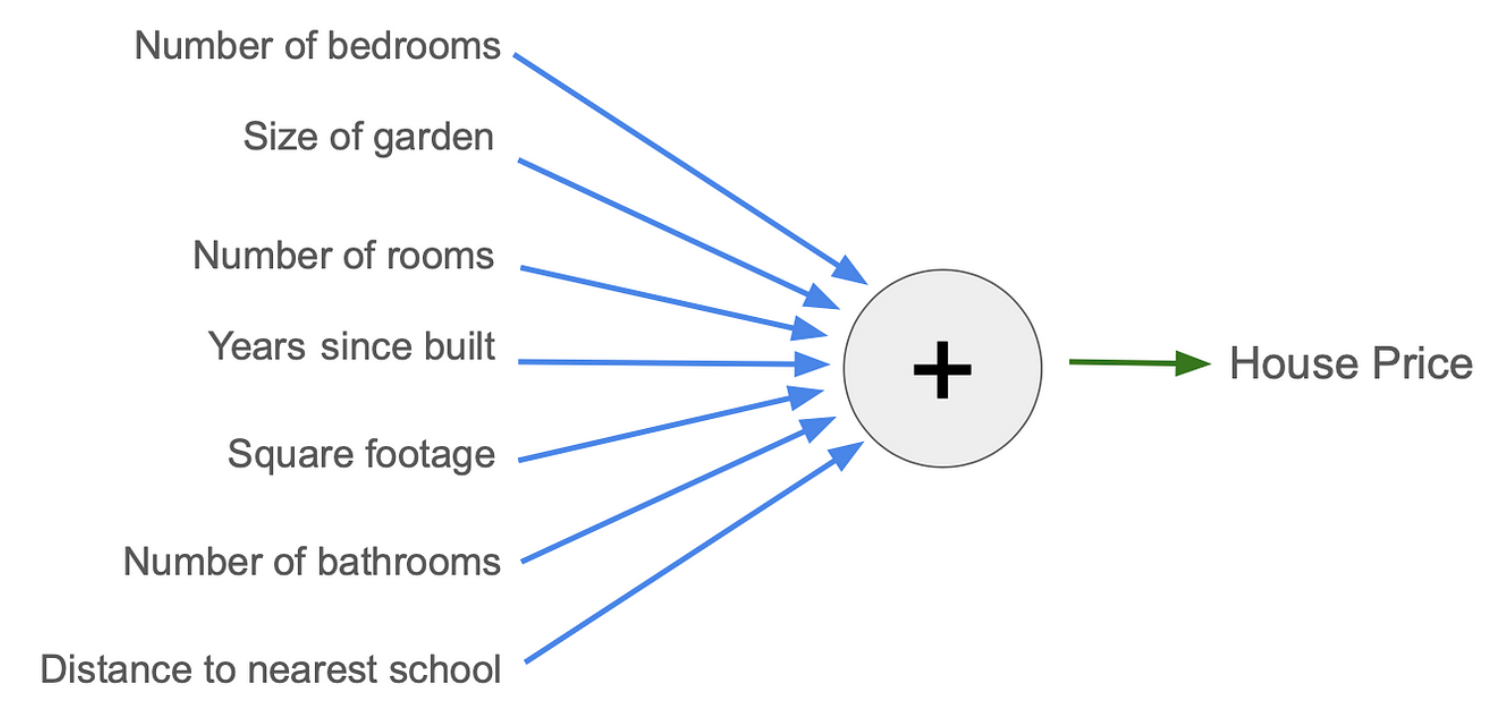
其中输入在左侧。每个蓝色箭头将输入乘以一个参数，然后所有参数相加，得出绿色箭头处的估计房价。此图中有 7个参数，可以一直调整这7个参数（蓝色箭头），直到找到一个好的模型。

因此，参数是模型内部的数字，我们可以调整它以使其生成的结果更准确或更不准确。并且我们希望使用7个输入使模型比只有1个或2个输入时更准确。

怎么衍生到神经网络？

LLM 是神经网络模型。神经网络模型的构建模块与我们目前用于估算房价的模型非常相似，它的构建方法是将许多这些简单模型排列成网格排列，并排列成包含节点的层。

这个神经网络模型有 3 层，有 7 个输入。第一层有 2 个节点，第二层有 5 个节点，最后一层有 1 个节点。每条蓝线都是一个参数。

相同点：与上一个模型一样，输入为7个，输出仍然是房价的估计值。

不同点：在于模型的复杂程度。这个神经网络内部有更多的步骤来将输入转换为输出。因此，我们希望这个更复杂的模型可以为我们提供更好的房价估计。与以前模型一样，每个参数都可以调整以使模型更好。

怎么衍生到大模型？

LLM 是大型神经网络，由许多输入和许多参数组成。LLM与我们的房价神经网络示例的主要区别在于：

• LLM 将单词作为输入和输出。
• LLM 的神经网络内部结构与上述示例不同，目前主流LL