BZOJ3240-NOI2013矩阵游戏

最新推荐文章于 2018-09-14 08:25:04 发布

JackflyDC

最新推荐文章于 2018-09-14 08:25:04 发布

阅读量341

点赞数 2

CC 4.0 BY-SA版权

分类专栏： OI

本文链接：https://blog.youkuaiyun.com/qq_34531807/article/details/81041711

OI 专栏收录该内容

222 篇文章

订阅专栏

本文提供了一种不使用矩阵乘法的方法来解决特定问题，并利用费马小定理处理大数计算。针对不同情况，推导了递推公式，并给出C++代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

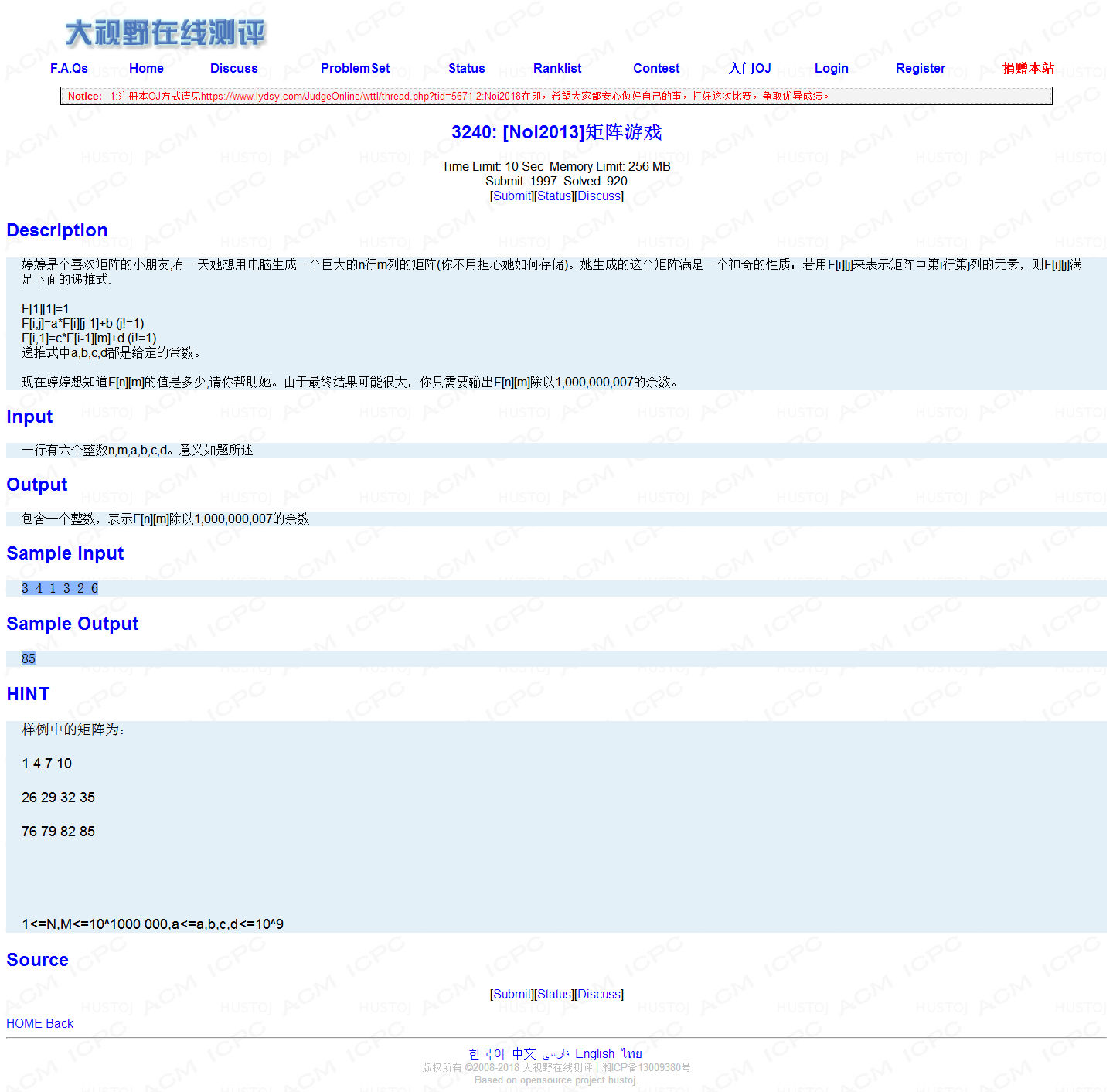
题解：
很多人都用矩乘来 $A$ 这道题，但据说矩乘可能会超时 $……$ 。
当 $a=1$ 时：
$F[i][j] = F[i][1] + (j − 1) ∗ b$
$F[i + 1][1] = c ∗ F[i][1] + (j − 1) ∗ b ∗ c + d$
当 $a\ne1$ 时：
$F[i][j] + λ = a ∗ (F[i][j − 1] + λ)$
$λ =\frac{b}{a-1}$
$F[i][j] = a^{j−1} ∗ (F[i][1] + λ) − λ$
$F[i + 1][1] = a^{m−1} ∗ c ∗ F[i][1] + b ∗ c ∗\frac{a^{m−1}−1}{a−1}+ d$
两式整理一下，发现同样的关系： $F[i + 1][1] = A ∗ F[i][1] + B$ ，计算方法同上。
算出 $F[n+1][1]$ ，减去 $d$ 再除 $c$ 即为 $F[n][m]$ 。
由于 $n$ 、 $m$ 的范围很大，需要使用费马小定理。
$Code：$

#include<bits/stdc++.h>
#define N 1000005
#define mod 1000000007
using namespace std;
typedef long long ll;
char s1[N],s2[N];
struct arr{ll uni,ord;}n,m;
ll a,b,c,d,p,k,t;
void give(char *s,arr &n)
{
    int p=strlen(s);
    for (int i=0;i<p;++i)
    {
        n.uni=(n.uni*10+s[i]-48)%mod;   
        n.ord=(n.ord*10+s[i]-48)%(mod-1);
    }
}
ll power(ll x,ll y)
{
    ll res=1ll;
    while (y)
    {
      if(y&1ll)res=res*x%mod;
      y=y/2ll;x=x*x%mod;
    }
    return res;
}
int main()
{
    scanf("%s%s",s1,s2);
    scanf("%lld%lld%lld%lld",&a,&b,&c,&d);
    give(s1,n);give(s2,m);
    if(a==1)
    {
        b=((m.uni-1)*b%mod*c+d)%mod;
        a=c;
    }else
    {
        k=b*power(a-1,mod-2)%mod;
        t=power(a,m.ord-1);
        a=c*t%mod;
        b=((t-1)*k%mod*c+d)%mod;
    }
    if(a==1)p=(1+n.uni*b)%mod;else
    {
        k=b*power(a-1,mod-2)%mod;
        t=power(a,n.ord);
        p=(t+(t-1)*k)%mod;
    }
    printf("%lld",((p-d)*power(c,mod-2)%mod+mod)%mod);
    return 0;
}