题目描述:

我的超时了,尽管使用了双向的bfs也是超时了
代码:
public boolean isEscapePossible(int[][] blocked, int[] source, int[] target) {
if(blocked == null || blocked.length == 0)
return true;
// 存放已经被封锁的
Set<Long> feng = new HashSet<>();
int mod = 1000000;
for (int [] tem : blocked) {
feng.add((long) (tem[0] * mod + tem[1]));
}
if(feng.contains((long)(source[0] * mod + source[1])) || feng.contains((long)(target[0] * mod + target[1]))){
return false;
}
int x[] = {0,0,1,-1};
int y[] = {1,-1,0,0};
Set<Long> isvisit = new HashSet<>();
Queue<int[]> queue1 = new LinkedList<>();
queue1.offer(new int[]{source[0],source[1]});
isvisit.add((long) (source[0] * mod + source[1]));
Set<Long> listqu1visit = new HashSet<>();
listqu1visit.add((long) (source[0] * mod+ source[1]));
Queue<int[]> queue2 = new LinkedList<>();
queue2.offer(new int[]{target[0],target[1]});
Set<Long> listqu2visit = new HashSet<>();
listqu2visit.add((long) (target[0] * mod+ target[1]));
isvisit.add((long) (target[0] * mod + target[1]));
while (!queue1.isEmpty() && !queue2.isEmpty()) {
int size = queue1.size();
int size2 = queue2.size();
if(size < size2){
for (int j = 0; j < size; j++) {
int ges[] = queue1.poll();
int temx = ges[0];
int temy = ges[1];
for (int i = 0; i < 4; i++) {
int x1 = temx + x[i];
int y1 = temy + y[i];
if(listqu2visit.contains((long) (x1 * mod + y1))){
return true;
}
if(x1 >= 0 && x1 < mod && y1 >= 0 && y1 < mod && !feng.contains(x1 + "" + y1) && !isvisit.contains(x1 + "" + y1)){
queue1.offer(new int[]{x1,y1});
listqu1visit.add((long) (x1 * mod + y1));
isvisit.add((long) (x1 * mod + y1));
}
}
}
}else {
for (int j = 0; j < size2; j++) {
int []ges = queue2.poll();
int temx = ges[0];
int temy = ges[1];
for (int i = 0; i < 4; i++) {
int x1 = temx + x[i];
int y1 = temy + y[i];
if(listqu1visit.contains((long) (x1 * mod + y1))){
return true;
}
if(x1 >= 0 && x1 < mod && y1 >= 0 && y1 < mod && !feng.contains(x1 + "" + y1) && !isvisit.contains(x1 + "" + y1)){
queue2.offer(new int[]{x1,y1});
listqu2visit.add((long) (x1 * mod + y1));
isvisit.add((long) (x1 * mod + y1));
}
}
}
}
}
return false;
}
参照别人的代码:
class Solution {
int dx[] = new int[]{0,0,1,-1};
int dy[] = new int[]{1,-1,0,0};
Set<Long> st = new HashSet<Long>();
public boolean isEscapePossible(int[][] b, int[] s, int[] t) {
for(int[] v:b){
long ck = (long)v[0]*(long)1000000+(long)v[1];
st.add(ck);
}
Queue<int[]> que = new LinkedList<>();
que.offer(s);
int d =1;
while(que.size()>0){
if(d==201){
return true;
}
int sz = que.size();
for(int i=0;i<sz;++i){
int go[] = que.poll();
if(go[0]==t[0]&&go[1]==t[1]) return true;
for(int ii=0;ii<4;++ii){
int nx = dx[ii]+go[0];
int ny = dy[ii]+go[1];
long ck = (long)nx*(long)1000000+(long)ny;
if(nx>=0&&ny>=0&&nx<1000000&&ny<1000000&&!st.contains(ck)){
st.add(ck);
que.offer(new int[]{nx,ny});
}
}
}
d++;
}
return false;
}
}
注意的是强制转成long必须这么写,可能我的这里强制转换出现了错误
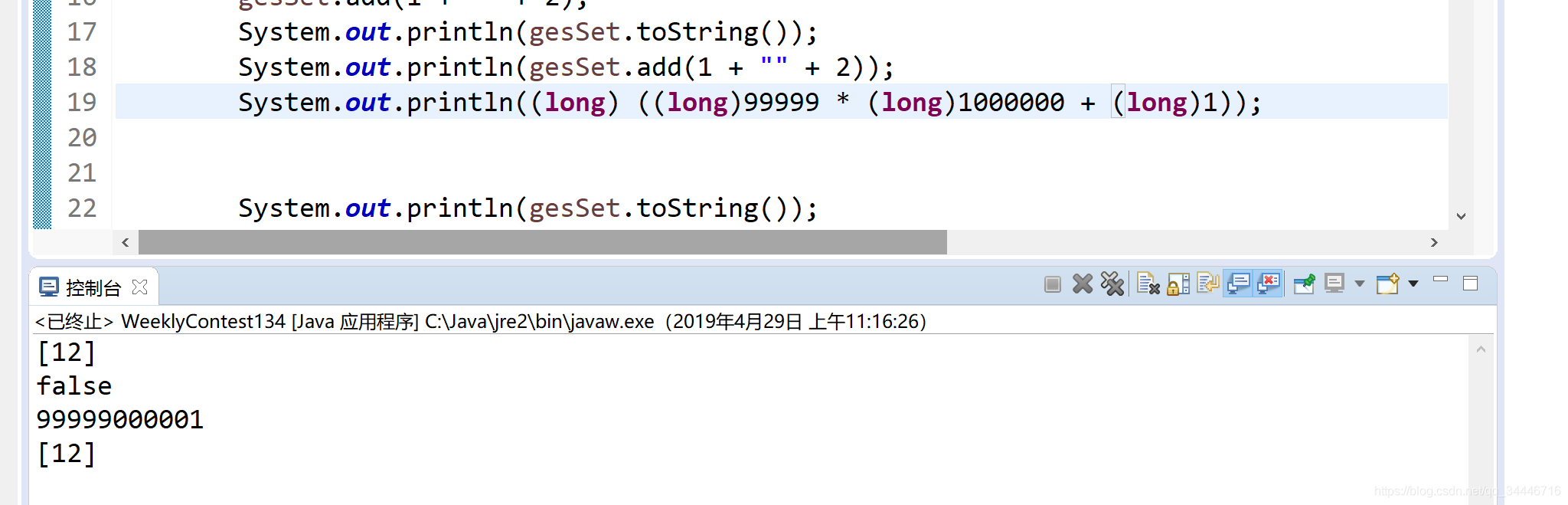
如果还是不清楚的话可以参照这个详细解释添加链接描述
具体如下:
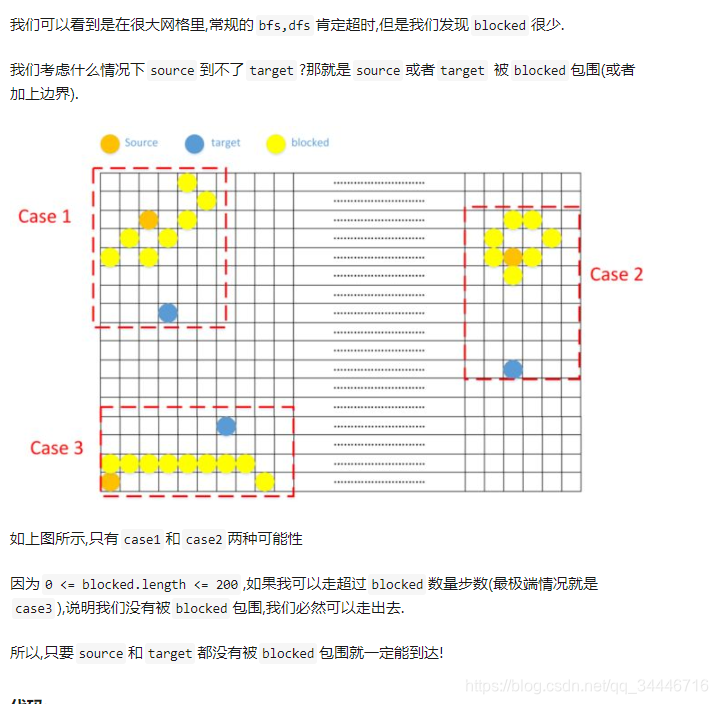








 探讨使用双向BFS算法解决迷宫中从源点到目标点的路径寻找问题,对比不同实现方式,分析超时原因及优化策略。
探讨使用双向BFS算法解决迷宫中从源点到目标点的路径寻找问题,对比不同实现方式,分析超时原因及优化策略。
















 467
467

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








