embedding发展史

1.文本多类分类

2.embedding

2.1 离散型

2.1.1 one-hot

2.1.2 词袋

2.1.3 TF-IDF

2.1.4 n-gram

n-gram介绍：
https://zhuanlan.zhihu.com/p/32829048
https://www.jianshu.com/p/c13b9468a924

数据稀疏问题：
https://www.jianshu.com/p/c13b9468a924
无论是原始的语言模型还是n-gram都是采用极大似然估计来估计概率值，即通过统计频次来近似概率值，统计频次极有可能统计不到较长句子的频次。比如在bi-gram模型下，在对语料进行统计时没有统计到“喜大”和“普奔”没有同时出现过，可是在计算语句概率时需要计算”我喜大普奔”这句话出现的概率，然而P(“普奔”|“喜大”)的概率为0（因为没有同时出现过），那么句子的概率为P(”我喜大普奔”) = p(“我”|<开始>) * p(“喜大”|“我”) * p(“普奔”|“喜大”) 经过连乘后概率为0，这样并不对。
解决措施（平滑技术）：
https://zhuanlan.zhihu.com/p/96826160
https://blog.youkuaiyun.com/tianyouououou/article/details/95591532
《统计自然语言处理》

n的大小对n-gram性能的影响：
n越大：对一下个词的约束就更强，理论上越精确，但是计算量更大，模型更复杂，并且精度提升的不够明显，所以在实际的任务中很少使用n>=4的语言模型。并且可能的n-gram数量是词汇表V的指数倍，这会占据很大的存储空间。
n越小：数据稀疏问题相对于大n来讲并不是那么严重。

2.2 分布型

2.2.1 共现矩阵

2.2.2 NNLM

NNLM(Neural Network Language model)，03年提出，词向量是神经网络训练时的中间产物。

首先通过长度为n的前向窗口构造训练集，前向窗口的意思就是把窗口内的最后字/词当作需要预测的y，前面的当作输入x，因此在NNLM在提出时仅考虑通过预测单词的上文进行预测。
eg:“我在人民广场吃炸鸡”，这里假如按词划分：【“我”，“在”，“人民广场”，“吃”，“炸鸡”】，那么使用长度为3的窗口划分，会得到以下训练集：
【“我”，“在”，“人民广场（待预测）”】
【“在”，“人民广场”，“吃（待预测）“】
【”人民广场“，”吃“，”炸鸡（待预测）“】

得到训练集后，模型训练流程如下：

2.2.3 word2vec

谷歌2013年提出的Word2Vec是目前最常用的词嵌入模型之一。Word2Vec实际是一种浅层的神经网络模型，它有两种网络结构，分别是CBOW（Continues Bag of Words）连续词袋和Skip-gram。Word2Vec和上面的NNLM很类似，但比NNLM简单。

2.2.3.1 CBOW

CBOW获得中间词两边的的上下文，然后用周围的词去预测中间的词，把中间词当做y，把窗口中的其它词当做x输入，x输入是经过one-hot编码过的，然后进行词袋（求和）操作；然后将此时的向量乘以V*m的矩阵，这个【V，m】就是我们要的词向量矩阵；最后乘以【m，V】的矩阵并通过激活函数softmax，可以计算出词库中每个单词的概率，接下来的任务就是训练神经网络的权重，使得语料库中所有被预测单词的整体概率最大化。

CBOW和NNLM异同：
相同：
1.都是one-hot编码
2.词向量都是中间产物，且是静态的
区别：
1.NNLM是将one-hot编码contact，CBOW则是进行词袋
2.NNLM仅通过上文预测中心词，CBOW则是通过上下文预测中心词

2.2.3.2 skip-gram

Skip-Gram正好和CBOW相反，我们的输入是特定词， 输出是softmax概率排前n的n个词，n是上下文词数。对应的Skip-Gram神经网络模型输入层有1个神经元，输出层有词汇表大小个神经元。隐藏层的神经元个数我们可以自己指定。通过DNN的反向传播算法，我们可以求出DNN模型的参数，同时得到所有的词对应的词向量。这样当我们有新的需求，要求出某1个词对应的最可能的8个上下文词时，我们可以通过一次DNN前向传播算法得到概率大小排前8的softmax概率对应的神经元所对应的词即可。

因此在输入特定词的one-hot后，也就不需要进行词袋操作了，当然词向量仍然是V*m矩阵。

2.2.3.3 加速方法之哈夫曼树/层次softmax

（1）哈夫曼树回顾
这个加速方法的实现是通过哈夫曼树，首先复习下哈夫曼树的建立：
霍夫曼树的建立其实并不难，过程如下：

输入：权值为(w1,w2,…wn)的n个节点

输出：对应的霍夫曼树

1）将(w1,w2,…wn)看做是有n棵树的森林，每个树仅有一个节点。

2）在森林中选择根节点权值最小的两棵树进行合并，得到一个新的树，这两颗树分布作为新树的左右子树。新树的根节点权重为左右子树的根节点权重之和。

3） 将之前的根节点权值最小的两棵树从森林删除，并把新树加入森林。

4）重复步骤2）和3）直到森林里只有一棵树为止。

下面我们用一个具体的例子来说明霍夫曼树建立的过程，我们有(a,b,c,d,e,f)共6个节点，节点的权值分布是(20,4,8,6,16,3)。

首先是最小的b和f合并，得到的新树根节点权重是7.此时森林里5棵树，根节点权重分别是20,8,6,16,7。此时根节点权重最小的6,7合并，得到新子树，依次类推，最终得到下面的霍夫曼树。
　　　　
那么霍夫曼树有什么好处呢？一般得到霍夫曼树后我们会对叶子节点进行霍夫曼编码，由于权重高的叶子节点越靠近根节点，而权重低的叶子节点会远离根节点，这样我们的高权重节点编码值较短，而低权重值编码值较长。这保证的树的带权路径最短，也符合我们的信息论，即我们希望越常用的词拥有更短的编码。如何编码呢？一般对于一个霍夫曼树的节点（根节点除外），可以约定左子树编码为0，右子树编码为1.如上图，则可以得到c的编码是00。

在word2vec中，约定编码方式和上面的例子相反，即约定左子树编码为1，右子树编码为0，同时约定左子树的权重不小于右子树的权重。

（2）word2vec缺点以及如何加速
在传统的word2vec中，不管是CBOW还是skip-gram在隐藏层到输出层中都需要对V个参数进行softmax计算，而这种计算所有词导致计算量太大，哈夫曼树就是基于隐藏层到输出层的改进。

用哈夫曼树进行隐藏参到输出层的映射，具体通过单词在语料库中出现的频率构建哈夫曼树。

和之前的神经网络语言模型相比，我们的霍夫曼树的所有内部节点就类似之前神经网络隐藏层的神经元,其中，根节点的词向量对应输入的词向量，而所有叶子节点就类似于之前神经网络softmax输出层的神经元，叶子节点的个数就是词汇表的大小。在霍夫曼树中，隐藏层到输出层的softmax映射不是一下子完成的，而是沿着霍夫曼树一步步完成的，因此这种softmax取名为"Hierarchical Softmax"。

如何“沿着霍夫曼树一步步完成”呢？在word2vec中，我们采用了二元逻辑回归的方法，即规定沿着左子树走，那么就是负类(霍夫曼树编码1)，沿着右子树走，那么就是正类(霍夫曼树编码0)。判别正类和负类的方法是使用sigmoid函数，即：

$P(+)=\sigma (x_w^T\theta )=\frac{1}{1+e^{-x_w^T\theta }}$

其中$x_w$是当前内部节点的词向量，而θ则是我们需要从训练样本求出的逻辑回归的模型参数。

使用霍夫曼树有什么好处呢？ 首先，由于是二叉树，因此隐藏参到输出层的计算量由V变成了log2V。第二，由于使用霍夫曼树是高频的词靠近树根，这样高频词需要更少的时间会被找到，这符合我们的贪心优化思想。

容易理解，被划分为左子树而成为负类的概率为P(−)=1−P(+)。在某一个内部节点，要判断是沿左子树还是右子树走的标准就是看P(−),P(+)谁的概率值大。而控制P(−),P(+)谁的概率值大的因素一个是当前节点的词向量，另一个是当前节点的模型参数θ。

对于上图中的w2，如果它是一个训练样本的输出，那么我们期望对于里面的隐藏节点n(w,1)的P(−)概率大，n(w,2)的P(−)概率大，n(w,3)的P(+)概率大。

回到基于Hierarchical Softmax的word2vec本身，我们的目标就是找到合适的所有节点的词向量和所有内部节点θ, 使训练样本达到最大似然。那么如何达到最大似然呢？
　　　　
我们使用最大似然法来寻找所有节点的词向量和所有内部节点 $\theta$ 。先手上面的 $w$ 例子来看, 我们期望最大化下面的似然函数:
$$\prod _{i=1}^{3}P\left(n\left(w\right),i\right)=\left(1-\frac{1}{1+e^{-x_w^T{\theta }_1}}\right)\left(1-\frac{1}{1+e^{-x_w^T{\theta }_2}}\right)\frac{1}{1+e^{-x_w^T{\theta }_3}}$$
为了便于我们后面一般化的描述，我们定义输入的词为$w$,其从输入层词向量求和平均后的霍夫曼树根节点词向量为$x_w$, 从根节点到预测单词所在的叶子节点，包含的节点总数为 $l_w,w$ 在霍夫曼树中从根节点开始, 经过的第 $i$ 个节点表示为 $p_i^w$, 对应的霍夫曼编码为 d i w ∈ { 0 , 1 } d_{i}^{w} \in\{0,1\} diw​∈{0,1}, 而该节点对应的模型参数表示为${\theta }_i^w$，其中$i=1,2,...l_w-1$，其中$l_w$已经是叶子节点了，而模型参数仅仅针对于霍夫曼树的内部节点。

定义 $w$ 经过的霍夫曼树节点$j$的逻辑回归概率为 $P\left(d_j^w\mid x_w,{\theta }_{j-1}^w\right)$, 其表达式为:

$$P\left(d_j^w\mid x_w,{\theta }_{j-1}^w\right)=\{\begin{array}{ll}\sigma \left(x_w^T{\theta }_{j-1}^w\right)& d_j^w=0\\ 1-\sigma \left(x_w^T{\theta }_{j-1}^w\right)& d_j^w=1\end{array}$$

那么对于某一个输入$w$的目标输出词,其最大似然为：

$$\prod _{j=1}^{l_w-1}P\left(d_j^w\mid x_w,{\theta }_{j-1}^w\right)=\prod _{j=1}^{l_w-1}{\left[\sigma \left(x_w^T{\theta }_{j-1}^w\right)\right]}^{1-d_{ȷ}^u}{\left[1-\sigma \left(x_w^T{\theta }_{j-1}^w\right)\right]}^{d_j^w}$$

在word 2 vec中, 由于使用的是随机梯度上升法, 所以并没有把所有样本的似然乘起来得到真正的训练集最大似然, 仅仅每次只用一个样本更新梯度, 这样做的目的是减少梯度计算量。这样我们可以得到 $w$ 的对数似然函数 $L$ 如下:
$$L=\log \prod _{j=1}^{l_w-1}P\left(d_j^w\mid x_w,{\theta }_{j-1}^w\right)=\sum _{j=1}^{l_w-1}\left(\left(1-d_j^w\right)\log \left[\sigma \left(x_w^T{\theta }_{j-1}^w\right)\right]+d_j^w\log \left[1-\sigma \left(x_w^T{\theta }_{j-1}^w\right)\right]\right)$$
要得到模型中 $w$ 词向量和内部节点的模型参数 $\theta$, 我们使用梯度上升法即可。首先我们求㔍型参数 ${\theta }_{j-1}^w$ 的梯度:
$$\begin{array}{rl}\frac{\partial L}{\partial {\theta }_{j-1}^w}& =\left(1-d_j^w\right)\frac{(\sigma (x_w^T{\theta }_{j-1}^w)(1-\sigma \left(x_w^T{\theta }_{j-1}^w\right)}{\sigma \left(x_w^T{\theta }_{j-1}^w\right)}{x}_w-d_j^w\frac{(\sigma (x_w^T{\theta }_{j-1}^w)(1-\sigma \left(x_w^T{\theta }_{j-1}^w\right)}{1-\sigma \left(x_w^T{\theta }_{j-1}^w\right)}{x}_w\\ & =\left(1-d_j^w\right)\left(1-\sigma \left(x_w^T{\theta }_{j-1}^w\right)\right)x_w-d_j^w\sigma \left(x_w^T{\theta }_{j-1}^w\right)x_w\\ & =\left(1-d_j^w-\sigma \left(x_w^T{\theta }_{j-1}^w\right)\right)x_w\end{array}$$

同样的方法, 可以求出 $x_w$ 的梯度表达式如下:
$$\frac{\partial L}{\partial x_w}=\sum _{j=2}^{l_w}\left(1-d_j^w-\sigma \left(x_u^T{\theta }_{j-1}^w\right)\right){\theta }_{j-1}^w$$
有了梯度表达式, 我们就可以用梯度上升法进行迭代来一步步的求解我们需要的所有的 ${\theta }_{j-1}^w$ 和 $x_w$

（3）CBOW下的多层softmax
准备工作：定义词向量大小M，CBOW的上下文大小2c，根据单词出现频率建立一颗哈夫曼树。
输入：对上下文2c中的每个词进行M大小的随机初始化，然后对其加权求平均，得到中间词的词向量w
输出：中间词的在整个词库上的预测概率
过程：模型中霍夫曼树的每个内部节点的参数$\theta$和输入词向量w在整个训练过程中被更新，训练后的w就是我们要的词向量。因为w是加权平均获得的，因此w的具体更新为对上下文词content(w)中的词进行更新。

过程如下：

1. 基于语料训练样本建立霍夫曼树。
2. 随机初始化所有的模型参数 $\theta$, 所有的词向量 $w$
3. 进行梯度上升迭代过程, 对于驯练集中的每一个样本 $(\mathrm{context}(w),w)$ 做如下处理:
   a) $\mathrm{e}=0$, 计算 $x_w=\frac{1}{2c}{\sum }_{i=1}^{2c}{x}_i$
   b) for $\mathrm{j}=1$ to $l_w-1$, 计算:
   $$\begin{array}{c}f=\sigma \left(x_w^T{\theta }_{j-1}^w\right)\\ g=\left(1-d_j^w-f\right)\eta \\ e=e+g{\theta }_{j-1}^w\\ {\theta }_{j-1}^w={\theta }_{j-1}^w+g{x}_w\end{array}$$
   c) 对于 $\mathrm{con}text(w)$ 中的每一个词向量 $x_i$ (共 2 c个 $)$ 进行更新:
   $$x_i=x_i+e$$
   d) 如果梯度收敛，则结束梯度迭代，否则回到步骤3继续迭代。

（4）skip-gram下的多层softmax
输入：中心词w的随机初始化词向量，维度为M
输出：中间词的在整个词库上的预测概率
过程：模型中霍夫曼树的每个内部节点的参数$\theta$和输入词向量w在整个训练过程中被更新，训练后的w就是我们要的词向量。这里和CBOW不同的是对w的更新不是对输入的更新，而也是为对上下文词content(w)中的词进行更新，具体解释和过程如下：
通过梯度上升法来更新我们的 ${\theta }_{j-1}^w$ 和 $x_w$, 注意这里的 $x_w$ 周围有 $2c$ 个词向量, 此时如果我们期望 $P\left(x_i\mid x_w\right),i=1,2\dots 2c$ 最大。此时我们注意到由于上下文是相互的，在期望 $P\left(x_i\mid x_w\right),i=1,2\dots 2c$ 最大化的同时，反过来我们也期望 $P\left(x_w\mid x_i\right),i=1,2\dots 2$ c最大。那么是使用 $P\left(x_i\mid x_w\right)$ 好还是 $P\left(x_w\mid x_i\right)$ 好呢, word2vec使用了后者, 这样做的好处就是在一个迭代窗口内, 我们不是只更新 $x_w$ , 而是更新 $x_i,i=1,2\dots 2c$ 共 $2c$ 个词。这样整体的迭代会更加均衡，因为这个原因，Skip-Gram模型并没有和CBOW模型一样对输入进行迭代更新，而是对2c个输出进行迭代更新。

这里总结下基于Hierarchical Softmax的Skip-Gram模型算法流程, 梯度迭代使用了随机梯度上升法:

1. 基于语料训练样本建立霍夫曼树。

2. 随机初始化所有的模型参数 $\theta$, 所有的词向量 $w$,

3. 进行梯度上升迭代过程, 对于训练集中的毎一个样本 $(w,\mathrm{con}\mathrm{tex}t(w))$ 做如下处理:
   a) for $\mathrm{i}=1$ to $2\mathrm{c}$ :

   i) $e=0$

   ii)for $\mathrm{j}=1$ to $l_w$ - 1, 计算:
   $$\begin{array}{c}f=\sigma \left(x_i^T{\theta }_{j-1}^w\right)\\ g=\left(1-d_j^w-f\right)\eta \\ e=e+g{\theta }_{j-1}^w\\ {\theta }_{j-1}^w={\theta }_{j-1}^w+g{x}_i\end{array}$$

   iii)
   $$x_i=x_i+e$$
   b)如果梯度收敛，则结束梯度迭代，算法结束，否则回到步骤a继续迭代。

2.2.3.4 加速方法之负采样

使用哈夫曼树的缺点：
使用霍夫曼树来代替传统的神经网络，可以提高模型训练的效率。但是如果我们的训练样本里的中心词w是一个很生僻的词，那么就得在霍夫曼树中辛苦的向下走很久了。因此采用了另一种方法进行加速—负采样。
如何使用负采样进行word2vec？
比如我们有一个训练样本，中心词是$w,$它周围上下文共有$2c$个词，记为$context(w)$。由于这个中心词$w$,的确和$context(w)$相关存在，因此它是一个真实的正例。通过Negative Sampling采样, 我们得到neg个和 $w$ 不同的中心词 $w_i,i=1,2,\dots$ neg, 这样 $\mathrm{context}(w)$ 和 $w_i$ 就组成了neg个并不真实存在 的负例。利用这一个正例和neg个负例, 我们进行二元逻辑回归, 得到负采样对应每个词 $w_i$ 对应的模型参数 ${\theta }_i$, 和毎个词的词向量。因此二元逻辑回归神经元的个数 = 词的个数。但是同时更新的二元逻辑回归神经元的个数 = 0 ~ neg = neg + 1

从上面的描述可以看出，Negative Sampling由于没有采用霍夫曼树，每次只是通过采样neg个不同的中心词做负例，就可以训练模型，因此整个过程要比Hierarchical Softmax简单。

不过有两个问题还需要弄明白：1）如果通过一个正例和neg个负例进行二元逻辑回归呢？ 2） 如何进行负采样呢？

如何使用正例和负例进行二元逻辑回归？
Negative Sampling也是釆用了二元逻辑回归来求解模型参数, 通过负采样, 我们得到了neg个负例$\left(\mathrm{context}(w),w_i\right)i=1,2,\dots neg$。 为了统一描述, 我们将正例定义为 $w_0$ ；$w_i,i=1,2,\dots neg$为负例；正例的上下文定义为$content(w_0)$。

在逻辑回归中，我们的正例应该期望满足:
$$P\left(\mathrm{context}\left(w_0\right),w_i\right)=\sigma \left(x_{w0}^T{\theta }^{w_i}\right),y_i=1,i=0$$
我们的负例期望满足:
$$P\left(\mathrm{context}\left(w_0\right),w_i\right)=1-\sigma \left(x_{w_0}^T{\theta }^{w_i}\right),y_i=0,i=1,2,\dots neg$$
我们期望可以最大化下式:
$$\prod _{i=0}^{\text{neg }}P\left(\mathrm{context}\left(w_0\right),w_i\right)=\sigma \left(x_{w_0}^T{\theta }^{w_0}\right)\prod _{i=1}^{neg}\left(1-\sigma \left(x_{w_0}^T{\theta }^{w_i}\right)\right)$$
利用逻辑回归和上一节的知识, 我们容易写出此时模型的似然函数为:
$$\prod _{i=0}^{neg}\sigma {\left(x_{w_0}^T{\theta }^{w_i}\right)}^{y_i}{\left(1-\sigma \left(x_w^T{\theta }^{w_i}\right)\right)}^{1-y_i}$$
此时对应的对数似然函数为:
$$L=\sum _{i=0}^{neg}{y}_i\log \left(\sigma \left(x_{w0}^T{\theta }^{w_i}\right)\right)+\left(1-y_i\right)\log \left(1-\sigma \left(x_{w0}^T{\theta }^{w_i}\right)\right)$$

同样采用随机梯度上升法，仅仅每次只使用一个样本更新$x_{w_i}$,${\theta }_i$
首先我们计算 ${\theta }^{w_i}$ 的梯度:
$$\begin{array}{rl}\frac{\partial L}{\partial {\theta }^{w_i}}& =y_i\left(1-\sigma \left(x_{w0}^T{\theta }^{w_i}\right)\right)x_{w_0}-\left(1-y_i\right)\sigma \left(x_{w_0}^T{\theta }^{w_i}\right)x_{w_0}\\ & =\left(y_i-\sigma \left(x_{w_0}^T{\theta }^{w_i}\right)\right)x_{w_0}\end{array}$$
同样的方法, 我们可以求出 $x_{w_0}$ 的梯度如下:
$$\frac{\partial L}{\partial x^{w_0}}=\sum _{i=0}^{neg}\left(y_i-\sigma \left(x_{w0}^T{\theta }^{w_i}\right)\right){\theta }^{w_i}$$
有了梯度表达式, 我们就可以用梯度上升法进行迭代来一步步的求解我们需要的 $x_{w_0},{\theta }^{w_i},i=0,1,\dots neg$.

如何进行负采样？
现在我们来看看如何进行负采样，得到neg个负例。word2vec采样的方法并不复杂，如果词汇表的大小为V,那么我们就将一段长度为1的线段分成V份，每份对应词汇表中的一个词。当然每个词对应的线段长度是不一样的，高频词对应的线段长，低频词对应的线段短。每个词w的线段长度由下式决定：
$$\mathrm{len}(w)=\frac{\mathrm{count}(w)}{{\sum }_{u\in vocab}\mathrm{count}(u)}$$
在word2vec中, 分子和分母都取了 $3/4$ 次毎如下:
$$\mathrm{len}(w)=\frac{\mathrm{count}(w{)}^{3/4}}{{\sum }_{u\in \text{ vocab }}\mathrm{count}(u{)}^{3/4}}$$
在采样前, 我们将这段长度为 1 的线段划分成 $M$ 等份, 䢒里 $M>>V$, 这样可以保证毎个词对应的线段都会划分成对应的小块。而M份中的毎一份都会落在某一个词对应的线段上。在采样的时候, 我们只需要从 $M$ 个位置中采样出 $neg$ 个位置就行，此时采样到的毎一个位置对应到的线段所属的词就是我们的负例词。

在word2vec中，M取值默认为10^8。

CBOW-负采样

词向量的维度大小M；中间词$w_0$的上下文大小2c，记为$content(w_0)$；步长η；负采样的个数neg

输入：$content(w_0)$中词的向量
输出（中间产物）: 词汇表毎个词对应的模型参数 $\theta$, 所有的词向量 $x_w$
过程：输入上下文词向量，加权平均求出中间词向量，然后根据正负样例进行训练，最终对上下文的词向量以及二元逻辑回归的参数进行更新：

1. 随机初始化所有的模型参数 ${\theta }_1$, 所有的词向量 $w$
2. 进行梯度上升迭代过程, 对于训练集中的每一个样本 $\left(\mathrm{context}\left(w_0\right),w_0,w_1,\dots w_{neg}\right)$ 做如下处理:
   a) $\mathrm{e}=0$, 计算 $x_{w_0}=\frac{1}{2c}{\sum }_{i=1}^{2c}{x}_i$
   b) for $\mathrm{i}=0$ to neg, 计算:
   $$\begin{array}{rl}f& =\sigma \left(x_{w_0}^T{\theta }^{w_i}\right)\\ g& =\left(y_i-f\right)\eta \\ e& =e+g{\theta }^{w_i}\\ {\theta }^{w_i}& ={\theta }^{w_i}+g{x}_{w_0}\end{array}$$
   c) 对于 $\mathrm{context}(w)$ 中的每一个词向量 $x_k($ 共 $2\mathrm{c}$ 个)进行更新:
   $$x_k=x_k+e$$
   d) 如果梯度收敛, 则结束梯度迭代, 否则回到步骠3继续迭代。

skip-gram-负采样
词向量的维度大小M；中间词$w_0$的上下文大小2c，记为$content(w_0)$；步长η；负采样的个数neg
输入：$content(w_0)$的向量
输出（中间产物）: 词汇表每个词对应的模型参数 $\theta$, 所有的词向量 $x_w$
过程：将$content(w_0)$中的每个词与neg个二元逻辑回归进行计算，然后更新$content(w_0)$中词的词向量。

1. 随机初始化所有的模型参数 $\theta$, 所有的词向量 $w$
2. 进行梯度上升迭代过程, 对于训练集中的每一个样本 $\left(\mathrm{context}\left(w_0\right),w_0,w_1,\dots w_{neg}\right)$ 做如下处理:
   a) for $i=1$ to $2c$ :
   i) $\mathrm{e}=0$
   ii) for $\mathrm{j}=0$ to neg, 计算:
   $$\begin{array}{c}f=\sigma \left(x_{w_{0i}}^T{\theta }^{w_j}\right)\\ g=\left(y_j-f\right)\eta \\ e=e+g{\theta }^{w_j}\\ {\theta }^{w_j}={\theta }^{w_j}+g{x}_{w_{0i}}\end{array}$$
   iii) 词向量更新:
   $$x_{w_{0i}}=x_{w_{0i}}+e$$
   b)如果梯度收敛，则结束梯度迭代，算法结束，否则回到步骤a继续迭代。

2.2.4 fastText

fastText和word2vec作者是同一个人，所以fastText和word2vec之间也很相似。

fastText是一个文本分类模型，输出是文本的类别的概率，文本的Embedding随着模型的训练被优化。首先fastText也是由输入层、隐藏层、输出层构成，输入层的输入是句子中的单词以及单词的n-gram特征的向量（随机Embedding）表示，将这些表示叠加取平均（词袋思想）。

n-gram特征是什么：
n-grams来表示一个单词：对于单词“book”，假设n的取值为3，则它的trigram特征有:

“<bo”, “boo”, “ook”, “ok>”

其中，<表示前缀，>表示后缀。于是，我们可以用这些trigram来表示“book”这个单词，进一步，我们可以用这4个trigram的向量叠加来表示“book”的词向量

利用n-gram特征表示一个单词的意义/优点是什么：
1.加强拥有公共字符特征的单词之间的联系/相似度：word2vec把语料库中的每个单词当成原子的，它会为每个单词生成一个向量。这忽略了单词内部的形态特征，比如：“book” 和“books”，“阿里巴巴”和“阿里”，这两个例子中，两个单词都有较多公共字符，即它们的内部形态类似，但是在传统的word2vec中，这种单词内部形态信息因为它们被当成不同的单词训练丢失了。
2.对于低频词生成的词向量效果会更好：因为它们的n-gram可以和其它词共享。
3.对于训练词库之外的单词，仍然可以构建它们的词向量：我们可以叠加它们的字符级n-gram向量。

模型隐层到输出层：
word2vec中通过哈夫曼树进行hierarchical softmax的操作在fastText的隐层到输出层也被应用了。在fastText的隐层到输出层的哈夫曼树中，叶子节点是类别，类别的权重是这个类别的数据在训练数据中出现的频率。

word2vec和fastText异同：
异：
输入：word2vec输入是目标单词的上下文，fastText的输入是多个单词及其n-gram特征
输出：word2vec的输出是目标词汇，fastText的输出是文档对应的类别
同：
图模型结构很像，都是采用embedding向量的形式，得到word的隐向量表达。
都采用很多相似的优化方法，比如使用Hierarchical softmax优化训练和预测中的计算速度。

fastText优点：
1.适合大型数据+高效的训练速度：能够训练模型“在使用标准多核CPU的情况下10分钟内处理超过10亿个词汇”
2.专注于文本分类，在许多标准问题上实现当下最好的表现（例如文本倾向性分析或标签预测）。

2.2.5 GloVe

GloVe的全称叫Global Vectors for Word Representation，它是一个基于全局词频统计（count-based & overall statistics）的词表征（word representation）工具，它可以把一个单词表达成一个由实数组成的向量，这些向量捕捉到了单词之间一些语义特性，比如相似性（similarity）、类比性（analogy）等。**我们通过对向量的运算，比如欧几里得距离或者cosine相似度，可以计算出两个单词之间的语义相似性。

GloVe通过共现矩阵实现，共现矩阵构建方法和上述的一样，只不过上述是统计两个词一起出现，即n-gram=2。

GloVe根据语料库（corpus）构建一个共现矩阵（Co-ocurrence Matrix）X，矩阵中的每一个元素 Xij 代表单词 i 和上下文单词 j 在特定大小的上下文窗口（context window）内共同出现的次数。这个次数是num，GloVe根据两个单词在上下文窗口的距离 d，提出了一个衰减函数（decreasing weighting）：decay=num/d 用于计算权重，也就是说距离越远的两个单词所占总计数（total count）的权重越小。

论文的作者提出以下的公式可以近似地表达词向量（Word Vector）和共现矩阵（Co-ocurrence Matrix）之间的近似关系：

因此损失函数为：

$J={\sum }_{i,j=1}^{V}f\left(X_{ij}\right){\left(w_i^T{\tilde{w}}_j+b_i+{\tilde{b}}_j-\log \left(X_{ij}\right)\right)}^2$

这个loss function的基本形式就是最简单的mean square loss，只不过在此基础上加了一个权重函数$f(X_{ij})$，那么这个函数起了什么作用，为什么要添加这个函数呢？我们知道在一个语料库中，肯定存在很多单词他们在一起出现的次数是很多的（frequent co-occurrences），那么我们希望：

1.这些单词的权重要大于那些很少在一起出现的单词（rare co-occurrences），所以这个函数要是非递减函数（non-decreasing）,即随着出现次数，权重增加或不减；
2.但我们也不希望这个权重过大（overweighted），当到达一定程度之后应该不再增加；
3.如果两个单词没有在一起出现，也就是，那么他们应该不参与到 loss function 的计算当中去，也就是f(x) 要满足 f(0)=0。
满足以上三个条件的函数有很多，论文作者采用了如下形式的分段函数：

虽然很多人声称GloVe是一种无监督（unsupervised learing）的学习方式（因为它确实不需要人工标注label），但其实它还是有label的，这个label就是以上公式中的 log(Xij)，而公式中的向量 $w和\tilde{w}$ 就是要不断更新/学习的参数，所以本质上它的训练方式跟监督学习的训练方法没什么不一样，都是基于梯度下降的。

具体地，这篇论文里的实验是这么做的：采用了AdaGrad的梯度下降算法，对矩阵 X 中的所有非零元素进行随机采样，学习曲率（learning rate）设为0.05，在vector size小于300的情况下迭代了50次，其他大小的vectors上迭代了100次，直至收敛。 最终学习得到的是两个vector是 $w和\tilde{w}$，因为 X 是对称的（symmetric），所以从原理上讲 $w和\tilde{w}$ 是也是对称的，他们唯一的区别是初始化的值不一样，而导致最终的值不一样。

所以这两者其实是等价的，都可以当成最终的结果来使用。但是为了提高鲁棒性，我们最终会选择两者之和 **作为最终的vector（两者的初始化不同相当于加了不同的随机噪声，所以能提高鲁棒性）

GloVe和word2vec相比：
1.Glove更容易并行化
2.word2vec的没有全局的共现，而GloVe可以有全局的共现（n-gram等于句长，然后根据距离用衰减函数）。个人理解：word2vec中一个单词虽然可以由上下文表示，但只是这条句子中的上下文，因此是局部的，而GloVe统计共现矩阵时候是按全局统计的。

2.2.6 ELMO

ELMO是“Embedding from Language Models”的简称，其实这个名字并没有反应它的本质思想，提出ELMO的论文题目：“Deep contextualized word representation”更能体现其精髓，而精髓在哪里？在deep contextualized这个短语，一个是deep，一个是context，其中context更关键。

在此之前的Word Embedding本质上是个静态的方式，所谓静态指的是训练好之后每个单词的表达就固定住了，以后使用的时候，不论新句子上下文单词是什么，这个单词的Word Embedding不会跟着上下文场景的变化而改变，所以对于比如Bank这个词，它事先学好的Word Embedding中混合了几种语义 ，在应用中来了个新句子，即使从上下文中（比如句子包含money等词）明显可以看出它代表的是“银行”的含义，但是对应的Word Embedding内容也不会变，它还是混合了多种语义。这是为何说它是静态的，这也是问题所在。

ELMO的本质思想是：我事先用语言模型（word2vec）学好一个单词的Word Embedding，此时多义词无法区分，不过这没关系。在我实际使用Word Embedding的时候，已经是在下游任务中了，此时有了实际的下游任务的数据，单词已经具备了特定的上下文了，这个时候我可以根据上下文单词的语义去调整单词的Word Embedding表示，这样经过调整后的Word Embedding更能表达在这个上下文中的具体含义，自然也就解决了多义词的问题了。所以ELMO本身是个根据当前上下文对Word Embedding动态调整的思路。

ELMO怎样使用：首先用训练好的词向量（word2vec）初始化ELMO的输入，然后ELMO在任务数据集上进行训练（ELMO训练）；最后使用ELMO的输出（Embedding）作为下游任务的词向量进行下游任务的训练（下游任务训练）。这样来看，ELMO整个的使用过程有点类似与预训练---->下游任务微调。

ELMO结构如下：

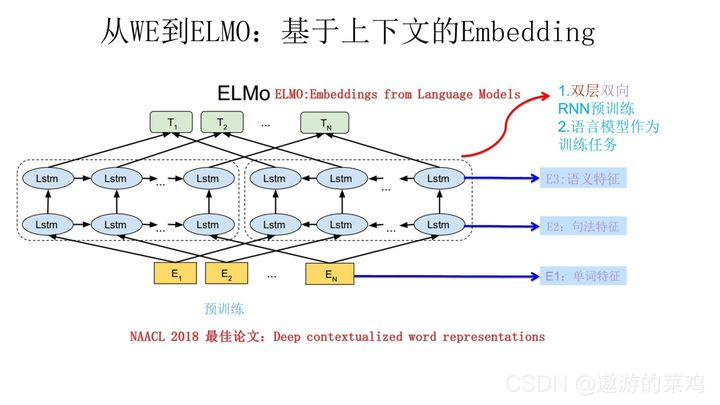
它的网络结构采用了双层双向LSTM，目前语言模型训练的任务目标是根据单词 $W_i$的上下文去正确预测单词$W_i$ ， $W_i$之前的单词序列Context-before称为上文，之后的单词序列Context-after称为下文。也就是这双层双向LSTM才使得Embedding有了当前语境的上下文信息！！！

图中最下面的黄色模块是word2vec作为输入传进去，然后上面的蓝色模块中左端的前向双层LSTM代表正方向编码器，输入的是从左到右顺序的除了预测单词外$W_i$ 的上文Context-before；右端的逆向双层LSTM代表反方向编码器，输入的是从右到左的逆序的句子下文Context-after；每个编码器的深度都是两层LSTM叠加。

这个网络结构其实在NLP中是很常用的。使用这个网络结构利用大量语料做语言模型任务就能预先训练好这个网络，如果训练好这个网络后，输入一个新句子，句子中每个单词都能得到对应的三个Embedding:

最底层是单词的Word Embedding；
往上走是第一层双向LSTM中对应单词位置的Embedding，这层编码单词的句法信息更多一些；
再往上走是第二层双向LSTM中对应单词位置的Embedding，这层编码单词的语义信息更多一些。
也就是说，ELMO的预训练过程不仅仅学会单词的Word Embedding，还学会了一个双层双向的LSTM网络结构，而这3个Embedding作为额外的特征输入到下游任务中。

上面介绍的是ELMO的第一阶段：预训练阶段。那么预训练好网络结构后，如何给下游任务使用呢？下面的图展示了下游任务的使用过程：

比如我们的下游任务仍然是QA问题：
1.此时对于问句X，我们可以先将句子X作为预训练好的ELMO网络的输入，这样句子X中每个单词在ELMO网络中都能获得对应的三个Embedding；
2.之后给予这三个Embedding中的每一个Embedding一个权重a，这个权重可以学习得来，根据各自权重累加求和，将三个Embedding整合成一个。那么具体是这样的：将3个Embedding输入到下游任务中，然后下游任务初始化一个3个权重相等的可训练的参数矩阵，将3个Embedding与这个参数矩阵相乘再相加就得到了Embedding_ELMO，然后每个单词的Embedding_ELMO是作为额外特征，也就是说每个单词的Embedding_ELMO与单词输入到下游任务中的Emedding进行拼接才最后构成了这个单词的Embedding。这是论文中的做法，关于为什么不直接用Embedding_ELMO而是将其作为额外特征这个不太理解。
3.然后将整合后的这个Embedding作为X句在自己任务的那个网络结构中对应单词的输入，以此作为补充的新特征给下游任务使用。对于上图所示下游任务QA中的回答句子Y来说也是如此处理。
因为ELMO给下游提供的是每个单词的特征形式，所以这一类预训练的方法被称为“Feature-based Pre-Training”。

前面我们提到静态Word Embedding无法解决多义词的问题，那么ELMO引入上下文动态调整单词的embedding后多义词问题解决了吗？解决了，而且比我们期待的解决得还要好。 对于Glove训练出的Word Embedding来说，多义词比如play，根据它的embedding找出的最接近的其它单词大多数集中在体育领域，这很明显是因为训练数据中包含play的句子中体育领域的数量明显占优导致，然而其他领域的词就比较少，比如“演出”；而使用ELMO，根据上下文动态调整后的embedding不仅能够找出对应的“演出”的相同语义的句子，而且还可以保证找出的句子中的play对应的词性也是相同的，这是超出期待之处。之所以会这样，是因为我们上面提到过，第一层LSTM编码了很多句法信息，这在这里起到了重要作用。

ELMO有什么值得改进的缺点呢？
首先，一个非常明显的缺点在特征抽取器选择方面，ELMO使用了LSTM而不是新贵Transformer，因此不能并行计算。Transformer是谷歌在17年做机器翻译任务的“Attention is all you need”的论文中提出的，引起了相当大的反响，很多研究已经证明了Transformer提取特征的能力是要远强于LSTM的。如果ELMO采取Transformer作为特征提取器，那么估计Bert的反响远不如现在的这种火爆场面。
另外一点，ELMO采取双向拼接这种融合特征的能力可能比Bert一体化的融合特征方式弱，但是，这只是一种从道理推断产生的怀疑，目前并没有具体实验说明这一点。

2.2.7 transformer

2.2.7.1 transformer基础

《Attention Is All You Need》是一篇Google提出的将Attention思想发挥到极致的论文。这篇论文中提出一个全新的模型，叫 Transformer，抛弃了以往深度学习任务里面使用到的 CNN 和 RNN。目前大热的Bert就是基于Transformer构建的，这个模型广泛应用于NLP领域，例如机器翻译，问答系统，文本摘要和语音识别等等方向。

2.2.7.1.1 transformer结构

Transformer模型中也采用了 encoer-decoder 架构。论文中encoder层由6个encoder堆叠在一起，decoder层也一样

其中每个ENCODER由两层组成：self-attention层和前馈神经网络层；
每个DECODER层由三层组成：self-attention层、Encoder-Decoder-attention层、前馈神经网络层

2.2.7.1.2 代入数据理解

首先，模型需要对输入的数据进行一个embedding操作，也可以理解为类似w2c的操作，enmbedding结束之后，输入到encoder层，self-attention处理完数据后把数据送给前馈神经网络，前馈神经网络的计算可以并行，得到的输出会输入到下一个encoder。

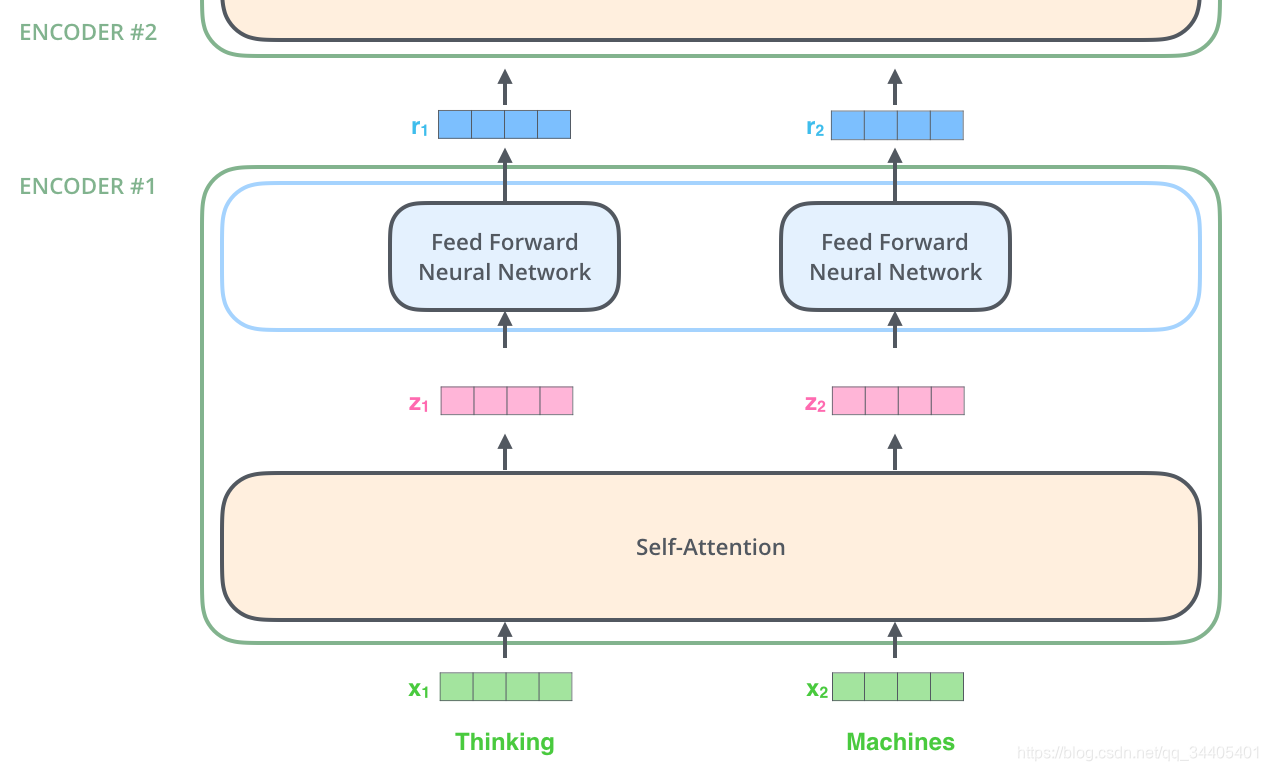
然而光有数据本身的mebedding不够，transformer模型中缺少一种解释输入序列中单词顺序的方法，它跟序列模型还不一样。为了处理这个问题，transformer给encoder层和decoder层的输入添加了一个额外的向量Positional Encoding，维度和embedding的维度一样，这个向量采用了一种很独特的方法来让模型得到到这个值，这个向量能决定当前词的位置，或者说在一个句子中不同的词之间的距离。这个位置向量的具体计算方法有很多种，论文中Positional Encoding的计算方法如下：

$PE(pos,2i)=\sin \left(\frac{\text{ pos }}{10000^{\frac{2i}{d_{\text{model }}}}}\right)$

$PE(pos,2i+1)=\cos \left(\frac{\text{ pos }}{10000^{\frac{2i}{d_{\text{model }}}}}\right)$

其中pos是指当前词在句子中的位置；i是指向量中每个值的index，可以看出，在偶数位置，使用正弦编码，在奇数位置，使用余弦编码；$d_{model}$是向量维度；为了计算方便，Transformer模型中通过三角函数采用绝对位置编码，即对每一个单词的每一个维度，都给定绝对的数值，模型不需要学习就可得到编码信息。从公式中的pos和i得知，这种编码方式既能表示相对位置，又能够表示绝对位置。

最后把这个Positional Encoding与embedding的值相加，作为输入送到下一层。

数据输入到一个Encoder后首先进入的第一层是self-attention层，这里先看下self-attention是怎样计算的：
self-attention思想和attention类似，但是self-attention是Transformer用来将其他相关单词的“理解”转换成我们正在处理的单词的一种思路，我们看个例子：

The animal didn’t cross the street because it was too tired

这里的 it 到底代表的是 animal 还是 street 呢，对于我们来说能很简单的判断出来，但是对于机器来说，是很难判断的，self-attention就能够让机器把 it 和 animal 联系起来，接下来我们看下详细的处理过程。

1.首先，self-attention会计算出每条数据的三个新的向量，我们把这三个向量分别称为Query、Key、Value。这三个向量是用数据embedding向量分别与3个矩阵相乘 （矩阵乘法） 得到的结果，这3个矩阵是随机初始化的，假设数据维度是512，那么矩阵为（512，64），注意第1个维度需要和embedding的维度一样，其值在BP的过程中会一直进行更新，得到的Q、K、V这三个向量的维度是64。

2.计算self-attention的分数值，该分数值决定了当我们在某个位置encode一个词时，对输入句子的其他部分的关注程度。这个分数值的计算方法是Query与Key做 点乘 ，以下图为例，首先我们需要针对Thinking这个词，计算出其他词对于该词的一个分数值，首先是针对于自己本身即q1·k1，然后是针对于第二个词即q1·k2。

3.接下来，把点乘的结果除以一个常数，这里我们除以8（scaled），这个值一般是采用上文提到的矩阵的第2个维度的开方即64的开方8，当然也可以选择其他的值，然后把得到的结果做一个softmax的计算。得到的结果即是每个词对于当前位置的词的相关性大小，当然，当前位置的词相关性肯定会会很大。

4.下一步就是把Value和softmax得到的值进行相乘，并相加，得到的结果即是self-attetion在当前节点的值

5.总结：实际计算中，随机初始化Query, Key, Value的矩阵，然后把embedding的值与三个矩阵直接相乘，把得到的新矩阵 Q 与 K 相乘，除以一个常数，做softmax操作，最后乘上 V 矩阵。这种通过 query 和 key 的相似性程度来确定 value 的权重分布的方法被称为scaled dot-product attention。

上面是一个self-attention层计算的步骤，而在Encoder和Decoder层有一个multi-headed attention机制，该机制理解起来很简单，就是说不仅仅只初始化一组Q、K、V的矩阵，而是初始化多组，tranformer是使用了8组，所以最后得到的结果是8个矩阵，最终attention子层的结果是将8组计算结果地拼接。接下来降维，具体降维的过程是将拼接起来的矩阵再和一个矩阵相乘进行降维，这个降维的过程就是FFNN (Feed Forward Neural Network)子层的操作。具体计算过程如下：

两组self-attention的情况：

8组下得到的矩阵：

8组结果拼接，然后通过乘以1个矩阵的方式降维（前馈神经网络子层）

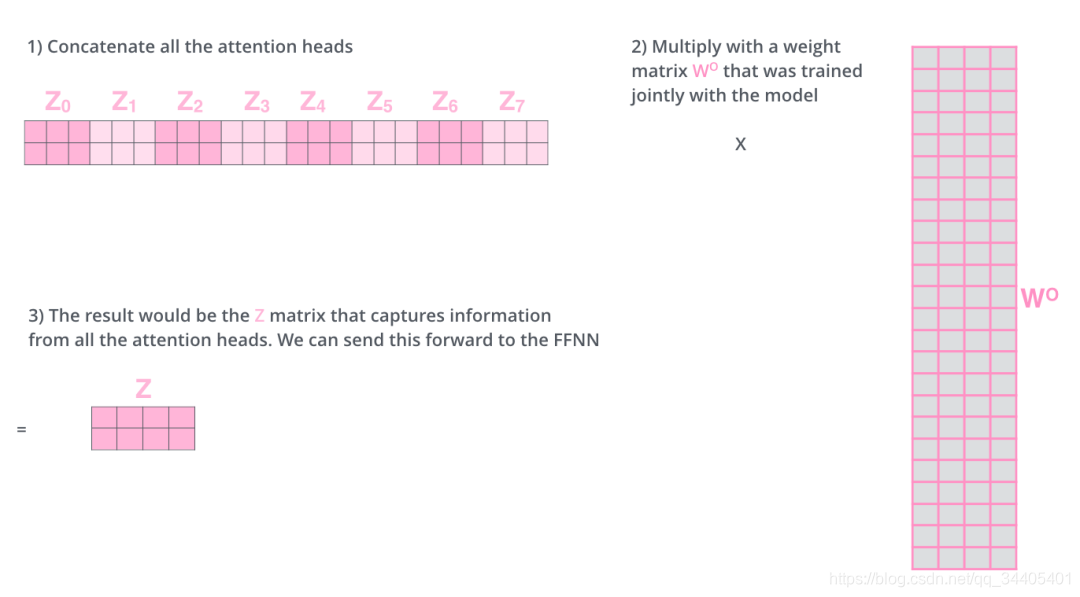
总结：

上面介绍了attention子层和FFNN子层的操作，但是这里要注意不管是Encoder还是Decoder，每个子层之间都会接一个残差模块，然后再接一个Layer normalization，也就是说经过attention后还得经过残差和Layer normalization才会进入FFNN

残差模块：
引入残差模块是为了避免出现网络层数加深，训练误差没有降低反而升高的情况：

右部的含义是直接将输入按照原样映射到输出，左部分就和VGG一样是堆叠的卷积层等，新的网络结构可以这样去理解，假设原来的网络不包含左部分，仅包含右部分，这可以理解为一个较浅的网络，这个时候加入左部分，整个网络的深度可以认为“没有加深”，而是在右部分直接映射的基础上增加了学习能力（因为网络参数更多，可以认为学习到了更多的信息），这样左右结合网络的学习能力就不会比仅有右部分的网络差。
这同样也可以换一个角度，用公式化的方式去理解，假设我们需要上述左右结合网络将输入x映射为H(x)，右部分是直接映射为x，那么左部分需要映射的值为F(x)=H(x)-x，作者认为通过训练网络学习残差F(x)要比学习H(x)简单，通过一个极端的例子：假如我们需要学习的H(x)就是输入到输出直接映射( H(x)=x )，那么左部分堆叠的网络层可以直接置0( F(x)=0 )。而在以前的网络中如果需要这种堆叠的网络层去学习直接映射的话是很困难的，因为激活函数会导致非线性（sigmoid激活函数）。
作者在数据集上做了测试，测试结果验证了实验假设，残差网络确实是一种更有效的模型。

Layer normalization：
Normalization有很多种，但是它们都有一个共同的目的，那就是把输入转化成均值为0方差为1的数据。我们在把数据送入激活函数之前进行normalization（归一化），因为我们不希望输入数据落在激活函数的饱和区。

Batch Normalization
BN的主要思想就是：在每一层的每一批数据上进行归一化。我们可能会对输入数据进行归一化，但是经过该网络层的作用后，我们的数据已经不再是归一化的了。随着这种情况的发展，数据的偏差越来越大，我的反向传播需要考虑到这些大的偏差，这就迫使我们只能使用较小的学习率来防止梯度消失或者梯度爆炸。BN的具体做法就是对每一小批数据，在批这个方向上做归一化。

Layer normalization
它也是归一化数据的一种方式，不过LN 是在每一个样本上计算均值和方差，而不是BN那种在批方向计算均值和方差！公式如下：

$LN\left(x_i\right)=\alpha \ast \frac{x_i-{\mu }_L}{\sqrt{{\sigma }_L^2+\epsilon }}+\beta$

以上是1个encoder的计算过程，1个Encoder的结构如下

详细：

上一个Encoder层的计算结果作为下一个Encoder层的输入进行计算，直到最后一个Encoder层。而最后一个Encoder层的输出有些不太一样，最后一个Encoder的输出并不是数据向量，而是一组注意力向量 K 和 V（个数等于头的个数）。这些注意力向量将会输入到每个解码器的Encoder-Decoder Attention层，这有助于解码器把注意力集中输入序列的合适位置。这里有个细节要注意下：最后一层编码器输出的 K、V向量是经过前馈层的，也就是说完整的经过了前馈层之后，再变换成K、V

下面看一个只有2层Encoder和Decoder的Transformer的静态结构图：

在完成了编码（encoding）阶段之后，我们开始解码（decoding）阶段。解码（decoding ）阶段的每一个时间步都输出一个翻译后的单词（这里的例子是英语翻译）。
接下来会重复这个过程，直到输出一个结束符，Transformer 就完成了所有的输出。每一步的输出都会在下一个时间步输入到下面的第一个解码器。Decoder 就像 Encoder 那样，从下往上一层一层地输出每一个时间步的结果。正对如编码器的输入所做的处理，我们把解码器的输入向量，也加上位置编码向量，来指示每个词的位置。当decoder层全部执行完毕后，怎么把得到的向量映射为我们需要的词呢，很简单，只需要在结尾再添加一个全连接层和softmax层，假如我们的词典是1w个词，那最终softmax会输入1w个词的概率，概率值最大的对应的词就是我们最终的结果。动态图如下：

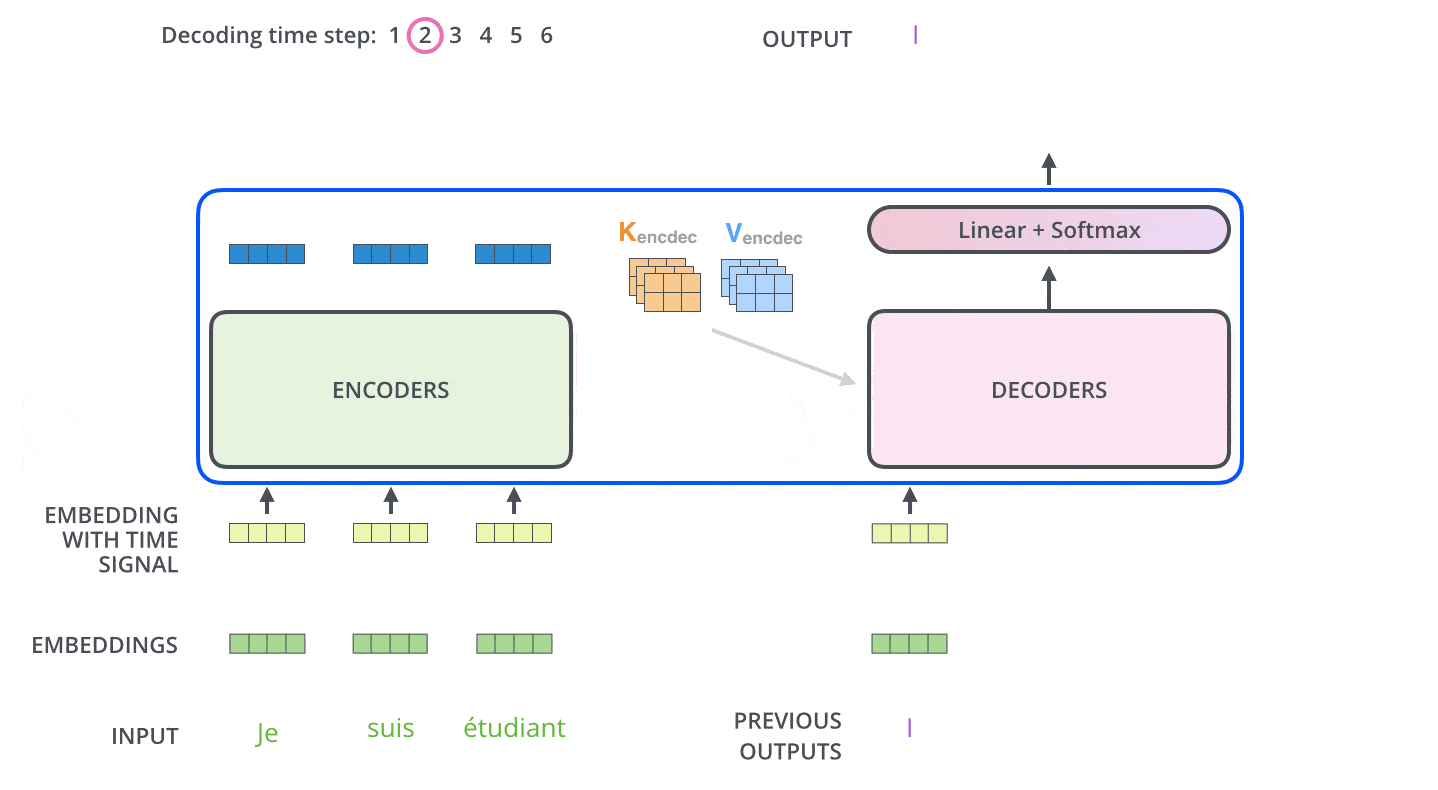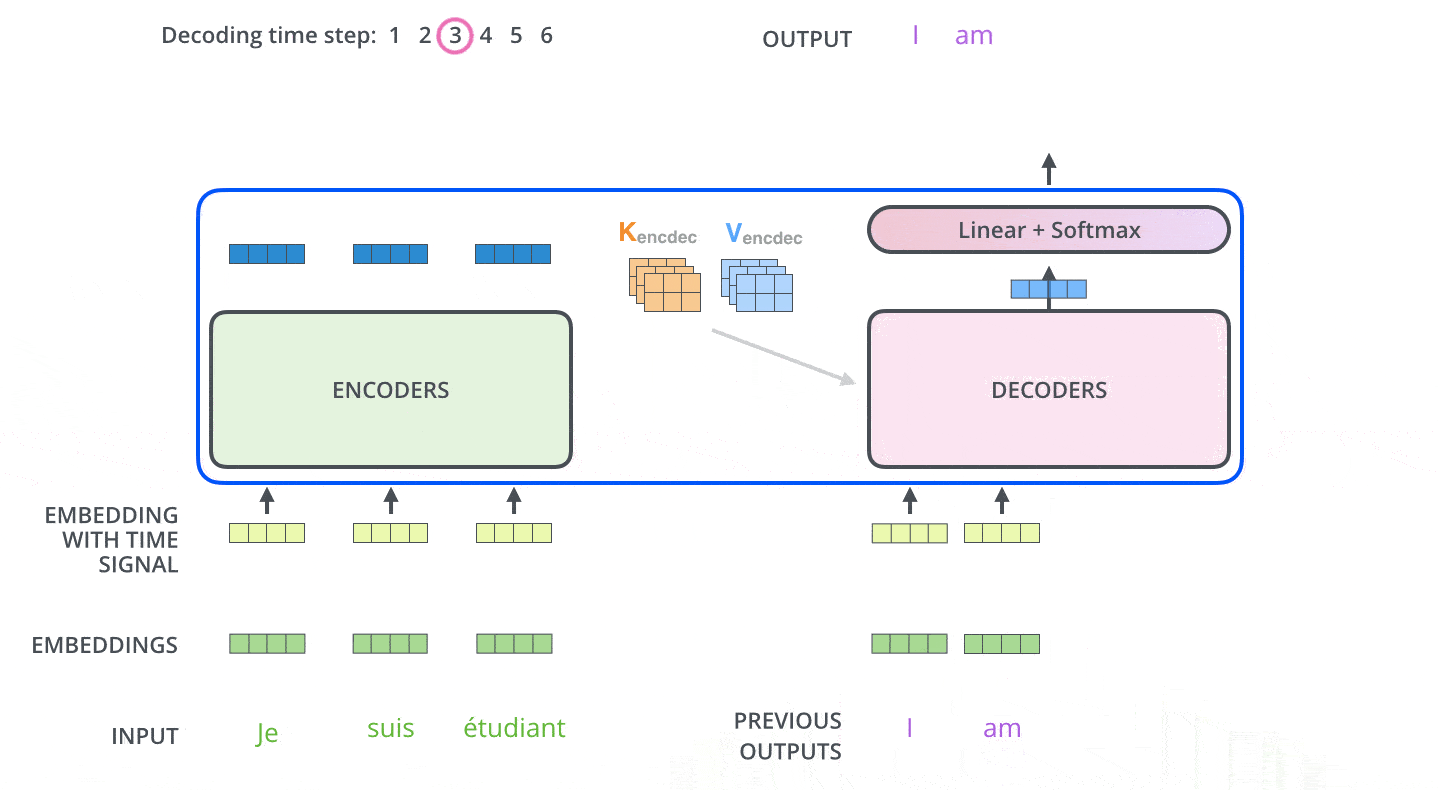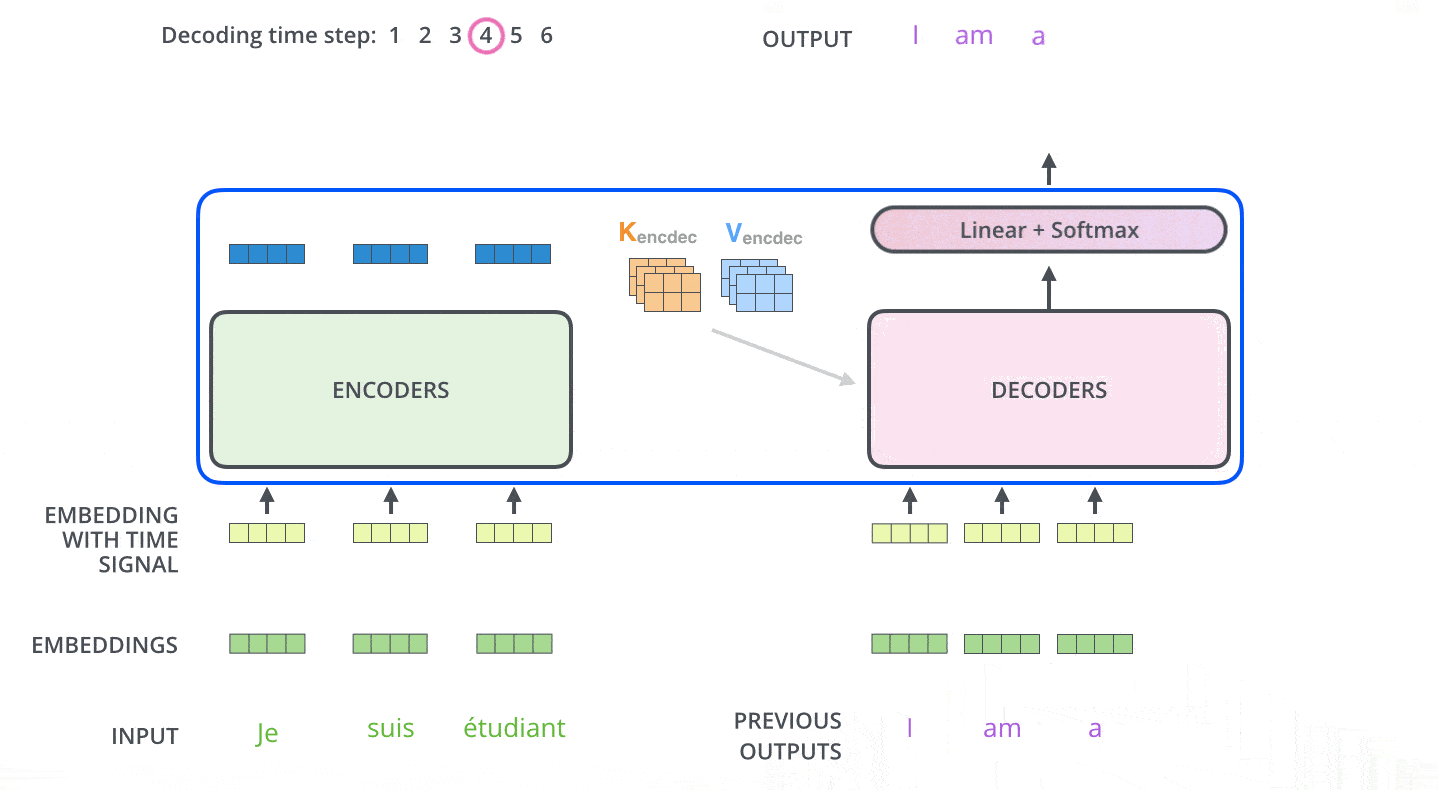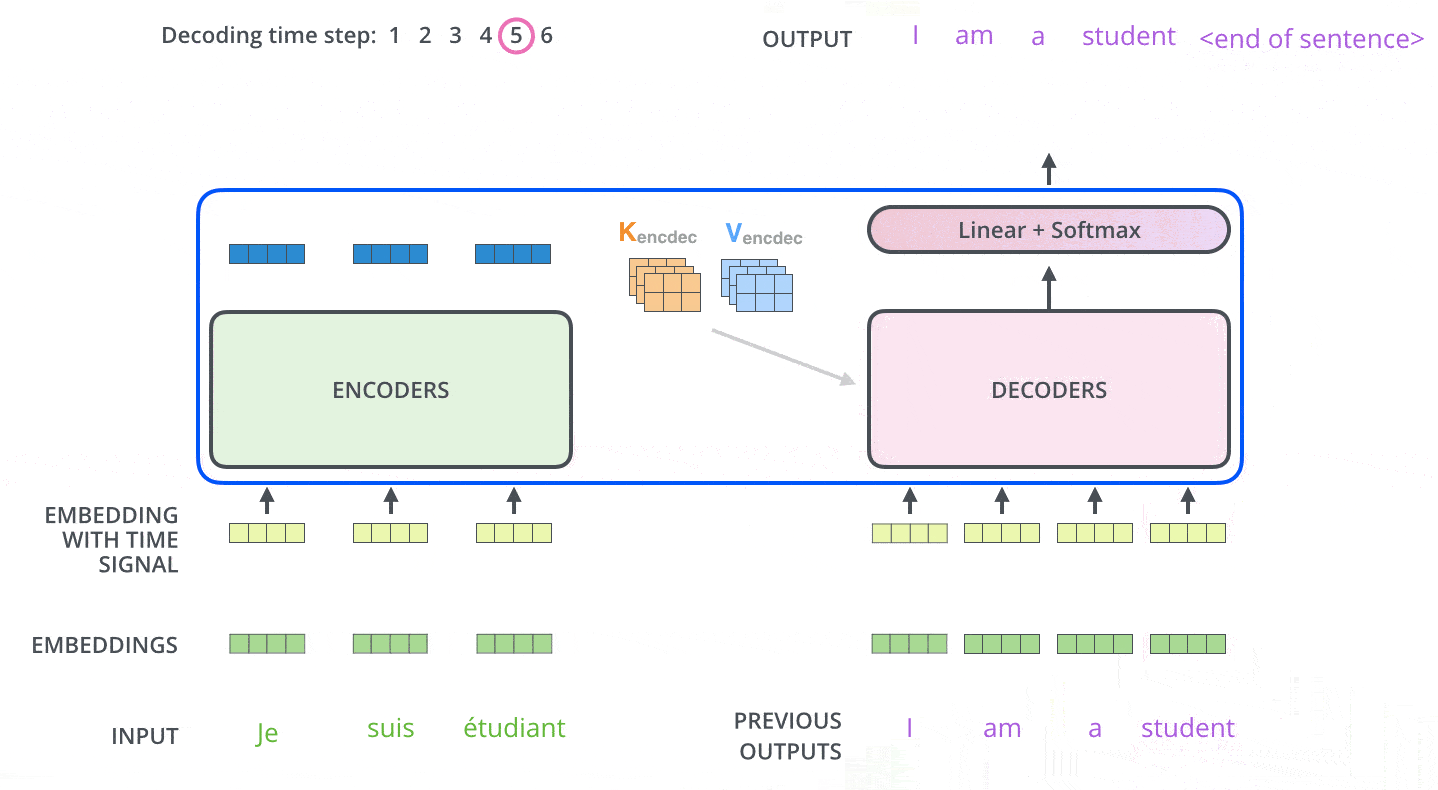
这里注意下Decoder层中的mask和Encoder有些不太一样，具体为训练和预测阶段不一样，首先介绍下mask的种类
Transformer 模型里面涉及两种 mask，分别是 padding mask 和 sequence mask。其中，padding mask 在所有的 scaled dot-product attention 里面都需要用到，而 sequence mask 只有在 decoder 的 self-attention 里面用到。
1.padding mask
什么是 padding mask 呢？因为每个批次输入序列长度是不一样的也就是说，我们要对输入序列进行对齐。具体来说，就是给在较短的序列后面填充 0。但是如果输入的序列太长，则是截取左边的内容，把多余的直接舍弃。因为这些填充的位置，其实是没什么意义的，所以我们的attention机制不应该把注意力放在这些位置上，所以我们需要进行一些处理。
具体的做法是，把这些位置的值加上一个非常大的负数(负无穷)，这样的话，经过 softmax，这些位置的概率就会接近0。
而我们的 padding mask 实际上是一个张量，每个值都是一个Boolean，值为 false 的地方就是我们要进行处理的地方。

2.Sequence mask
文章前面也提到，sequence mask 是为了使得 decoder 不能看见未来的信息。也就是对于一个序列，在 time_step 为 t 的时刻，我们的解码输出应该只能依赖于 t 时刻之前的输出，而不能依赖 t 之后的输出。因此我们需要想一个办法，把 t 之后的信息给隐藏起来。
那么具体怎么做呢？也很简单：产生一个上三角矩阵，上三角的值全为0。把这个矩阵作用在每一个序列上，就可以达到我们的目的。
对于 decoder 的 self-attention，里面使用到的 scaled dot-product attention，同时需要padding mask 和 sequence mask 作为 attn_mask，具体实现就是两个mask相加作为attn_mask。
其他情况，attn_mask 一律等于 padding mask

在训练阶段，我们知道未来的输出，因此需要用到sequence mask进行并行计算，而在预测阶段并不知道未来输出，并且依赖于上个单词的输出，因此不需要用到，因此也不能并行计算！！！

2.2.7.1.3 transformer问答

1.Transformer为什么需要进行Multi-head Attention

原论文中说到进行Multi-head Attention的原因是将模型分为多个头，形成多个子空间，可以让模型去关注不同方面的信息，最后再将各个方面的信息综合起来。其实直观上也可以想到，如果自己设计这样的一个模型，必然也不会只做一次attention，多次attention综合的结果至少能够起到增强模型的作用，也可以类比CNN中同时使用多个卷积核的作用，直观上讲，多头的注意力有助于网络捕捉到更丰富的特征/信息。

2.Transformer相比于RNN/LSTM，有什么优势？为什么？

• RNN系列的模型，并行计算能力很差。RNN并行计算的问题就出在这里，因为 T 时刻的计算依赖 T-1 时刻的隐层计算结果，而 T-1 时刻的计算依赖 T-2 时刻的隐层计算结果，如此下去就形成了所谓的序列依赖关系。而Transformer在Encoder阶段完全可以并行化计算，在decoder的训练阶段中也可以并行化计算

• Transformer的特征抽取能力比RNN系列的模型要好。

3.为什么说Transformer可以代替seq2seq？

seq2seq缺点：这里用代替这个词略显不妥当，seq2seq虽已老，但始终还是有其用武之地，seq2seq最大的问题在于将Encoder端的所有信息压缩到一个固定长度的向量中，并将其作为Decoder端首个隐藏状态的输入，来预测Decoder端第一个单词(token)的隐藏状态。在输入序列比较长的时候，这样做显然会损失Encoder端的很多信息，而且这样一股脑的把该固定向量送入Decoder端，Decoder端不能够关注到其想要关注的信息。

Transformer优点：transformer不但对seq2seq模型这两点缺点有了实质性的改进(mutli-attention子层)，而且还引入了Encoder-Decoder attention模块，让源序列和目标序列首先“自关联”起来，这样的话，源序列和目标序列自身的embedding表示所蕴含的信息更加丰富，而且后续的FFN层也增强了模型的表达能力，并且Transformer并行计算的能力是远远超过seq2seq系列的模型，因此我认为这是transformer优于seq2seq模型的地方。

4.decoder中encoder-decoder attention层的作用

decoder阶段中，每个时间步的输入信息有两个：encoder的输出、decoder上一个时间步的输出；其中encoder可以理解为LSTM中的细胞状态的信息，保存的是encoder端所有的信息。

拿到信息后，decoder进行的第一个操作是multi-head attention，这个子层的作用是模型考虑之前的输出进行当前的输出（训练阶段中通过上三角矩阵将当前时间步未来的信息mask，然后并行训练，预测过程中因为没有未来信息，因此是串行计算）。

接下来通过的是encoder-decoder attenion，这一部分可以看成解码器在用编码器的输出信息来计算当前解码应该输出什么，因为是通过Q、K、V形式考虑Encoder的全局信息，因此可以做到在每个时间步中动态的从全局信息中获取当前时间步想要的。其中Q来自之前的decoder层，K、V来自最后一层encoder的输出。

decoder经过mutli head-attention和encoder-decoder attention层后，就做到了考虑之前的输出信息、以及encoder全局的信息进行下一个时间步的输出。

5.scaled dot-product attention中的scaled

Transformer以及基于Transformer等的BERT之类的预训练模型都用的是 scaled dot-product attention，那么scaled是什么？有什么用？

根据上面的attention公式可知，scaled其实就是将QK结果除以$\sqrt{d_k}$，那么为什么这么做？论文中的解释就是点积后的结果和维度大小成正比（数据维度越大，结果越大），大值经过softmax后，其实分布已经更像one-hot分布了，梯度会变得很小，因此除以$\sqrt{d_k}$就是让attention权重分布方差为1，而不是dk，也就是让attention分布更平缓。 另一个角度理解：权重的初始化被假设为标准正态分布，经过注意力计算后，数据之间的点积变成了d_model个标准正态分布的加和，所以除以根号d_model使其尽可能再回标准正态分布。

下面看下大值对于softmax的影响/大值为什么会使softmax梯度变小：
对于一个输入向量 $\mathbf{x}\in {\mathbb{R}}^d$, softmax函数将其映射/归一化到一个分布 $\hat{\mathbf{y}}\in {\mathbb{R}}^d$ 。在这个过 程中, softmax先用一个自然底数 $e$ 将输入中的元素间差距先 “拉大"，然后归一化为一个分布。 假设某个输入 $\mathbf{x}$ 中最大的的元素下标是 $k$, 如果输入的数量级变大 (每个元素都很大)，那么 ${\hat{y}}_k$ 会非常接近 1 。
我们可以用一个小例子来看看 $\mathbf{x}$ 的数量级对输入最大元素对应的预测概率 ${\hat{y}}_k$ 的影响。假定输入 $\mathbf{x}=[a,a,2a{]}^{\top })$, 我们来看不同量级的 $a$ 产生的 ${\hat{y}}_3$ 有什么区别。

• $a=1$ 时, ${\hat{y}}_3=0.5761168847658291$
• $a=10$ 时, ${\hat{y}}_3=0.999909208384341$;
• $a=100$ 时, ${\hat{y}}_3\approx 1.0$ (计算机精度限制)。

以上结果也很好理解，指数爆炸嘛。

那么为什么除以的是根号k？
从attention计算公式可以看出，其值受Q、K的维度影响，而我们希望attention值仅和真实注意力分布有关，并不希望数据维度也可以影响，因此最后除以根号k消除维度的影响。

总结：因此可以看出，除以根号k的作用除了有防止大值梯度消失，还有消除数据维度影响的作用。

6.Transformer为什么不能处理长文档

self-attention结构，理论上能够对任意长的文本进行建模，但是self-attention结构也限制了实际能够处理的长度，因为其的时间空间复杂度都是平方级增长的（序列中每个都需要计算与其他的attention，相当于每个进行一次遍历序列，因此式平方），而又因为是多头机制，因此时间复杂度是O(hdn^2)， h 是注意力头的数量，d 是键向量和查询向量的维数，n 是序列的长度。
除此之外，空间复杂度也很高：$O\left(hdn+h{n}^2\right)$，其中hdn是h个头中n个词对应的QKV，hn^2是每个头中的每个词对应其他词的attetion得分。

所以在实际使用的时候，我们都会对长文档进行一些预处理，通常是把输入句子控制在某个最大长度(如bert最大长度限定512)。通过滑窗的方式将文章分段送入模型，然后将不同片段的输出合并起来做下游任务。

7.Transformer位置编码有什么问题

Transformer的位置编码因为是三角函数相对位置编码，因此输入长度上不会受编码的限制，但是也有一些其他的问题：1.无法体现方向；2.经过attention的一系列线性计算后，词与词之间的位置信息被减少。
BERT 虽然来自于 Transformer 的 Encoder 部分, 但是两者位置编码方式并不同, BERT 的位置编码是随机初始化 512 个位置编码向量,然后在模型中训练.而 Transformers 的位置编码是采用了三角函数:
$$\begin{array}{r}P{E}_{(\text{pos, }2i)}\mid =\sin \left(\text{ pos }/10000^{2i/d_{\text{model }}}\right)\\ P{E}_{(pos,2i+1)}\mid =\cos \left(\text{ pos }/10000^{2i/d_{\text{model }}}\right)\end{array}$$
相比于 BERT 初始定好的编码, 采用三角函数相对编码可以使输入不受位置编码的限制。
然而这种编码方式存在两个问题：1.无法体现方向； 2 .经过 attention 计算后无法体现两个单 词之间的相对距离。

首先看下没有经过 attention 时为什么三角函数可以捕获单词之间的相对位置信息:
$$\begin{array}{rl}\sin (\alpha +\beta )& =\sin (\alpha )\cos (\beta )+\cos (\alpha )\sin (\beta )\\ \cos (\alpha +\beta )& =\cos (\alpha )\cos (\beta )-\sin (\alpha )\sin (\beta )\end{array}$$
对于 pos 位置处的单词的词向量表示为 $PE($ pos $)$, 偏移 $\mathrm{k}$ 个位置后的向量表示为 $PE($ pos $+k)$, 那么 $PE(\mathrm{pos}+k)\cdot$ 可表示为如下:
$$\begin{array}{l}P{E}_{(pos+k,2i)}=P{E}_{(pos,2i)}\ast P{E}_{(k,2i+1)}+P{E}_{(pos,2i+1)}\ast P{E}_{(k,2i)}\\ P{E}_{(\text{pos }+k,2i+1)}=P{E}_{(pos,2i+1)}\ast P{E}_{(k,2i+1)}-P{E}_{(pos,2i)}\ast P{E}_{(k,2i)}\end{array}$$
因此 $PE($ pos $+k)$. 可看作 $PE($ pos $)$ 和 $PE(k)$ 的线性组合, $\mathrm{k}$ 可以表示两个单词之间的距 离信息, 因此 Transformer 模型可捕捉到两个单词之间的距离。而位置编码一般从 0 开始, 那么第 $\mathrm{k}$ 个位置就是 $0+\mathrm{k}$, 体现了 0 和 $\mathrm{k}$ 的相对位置编码信息。
那么为什么无法体现方向？
$\mathrm{x}$ 位置后得 $\mathrm{y}$ 和 $\mathrm{y}$ 位置后的 $\mathrm{x}$ 的距离编码一致，因此无法却分x是在y前还是y后:
$$\begin{array}{l}\cos (x-y)=\sin (x)\sin (y)+\cos (x)\cos (y)\\ \cos (y-x)=\sin (y)\sin (x)+\cos (y)\cos (x)\end{array}$$
因此无法体现方向。

而经过 attention 后无法体现词之间的相对位置距离的原因如下:
Self-Attention 计算公式如下:
$$\text{ Attention }=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$
其中 $\mathrm{Q},\mathrm{K},\mathrm{V}$ 分别等于输入 ${\mathrm{X}}^{\ast }\mathrm{Q},{\mathrm{X}}^{\ast }\mathrm{K},{\mathrm{X}}^{\ast }\mathrm{V}$, 输入 $\mathrm{X}$ 一般为 Embedding。不考虑最终能 attention 后的表示, 仅考虑 attention 得分计算, 且 $\mathrm{x}={\mathrm{x}}_{}$ word+x_pos, 那么第 $\mathrm{i}$ 个词和第 $\mathrm{j}$ 个词的 attention 值(末经过 softmax)为:
$$e_{ij}=\frac{\left(x_i{W}^Q\right){\left(x_j{W}^K\right)}^T}{\sqrt{d_z}}=\frac{\left(\left(x_i^{\text{word }}+x_i^{\text{position }}\right)W^Q\right){\left(\left(x_j^{\text{word }}+x_j^{\text{position }}\right)W^K\right)}^T}{\sqrt{d_z}}$$
然后将 $e_{ij}$ 执行 softmax, 即 ${\alpha }_{ij}=\frac{\exp e_{ij}}{{\sum }_{k=1}^n\exp e_{ik}}$, 然后根据 $\mathrm{V}$ 值加权计算, 即
$$z_i=\sum _{j=1}^n{\alpha }_{ij}\left(\left(x_j^{\text{word }}+x_j^{\text{position }}\right)W^V\right)=\sum _{j=1}^n{\alpha }_{ij}\left(x_j^{\text{word }}{W}^V+x_j^{\text{position }}{W}^V\right)$$
可以看到上述无论是 attention 得分的计算, 还是最后加权的计算都是 x_word+x_pos 然后通 过参数矩阵 (QKV) 经过一系列线性变化, 而这个参数矩阵是可训练的, 即参数矩阵更新时 是考虑 word 和 pos 信息进行更新的，因此无法有效的保留位置信息。

目前看到的一种改进做法就是将 word 和 pos 编码分割开独立进行 QKV 计算, 最后加在一 起, 然而这种只能解决经过 attention 后无法保留位置信息这个问题, 针对表示方向这个还 是无法解决。
因此, 还有一种做法: Relation-Aware-Self-Attention

《Self-Attention with Relative Position Representations》中将输入看做是有个有向的全连接图, 两个单词之间的边可利用向 $a_{ij}^V$ 和 $a_{ij}^K$ 来表示, 该 向量可以替代之前的位置向量, 并且是学习得到的。并且该向量在计算时不需要经过额外的 线性变换, 且在所 $\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{d}$ 中共享 (即 mutli-head 机制中不同的头用的是同一个位置编码)。个 更新后的 Attention 公式如下:
$$z_i=\sum _{j=1}^n{a}_{ij}\left(x_j{W}^V+a_{ij}^V\right)$$
其中， attention 得分 $e_{ij}$ 计算公式如下：
$$e_{ij}=\frac{\left(x_i{W}^Q\right){\left(x_j{W}^K+a_{ij}^K\right)}^T}{\sqrt{d_z}}$$
由 $e_{ij}$ 经过 softmax 得到 $a_{ij}$ 的过程照旧。
经过这种重新编码的方式, 很好的解决了方向以及 attention 抺消位置编码信息的两个问题。

2.2.7.2 vanilla Transformer

self-attention结构，理论上能够对任意长的文本进行建模，但是self-attention结构也限制了实际能够处理的长度，因为其的时间空间复杂度都是平方级增长的。

所以在实际使用的时候，我们都会对长文档进行一些预处理，通常是把输入句子控制在某个最大长度(如bert最大长度限定512)。通过滑窗的方式将文章分段送入模型，然后将不同片段的输出合并起来做下游任务。介绍如下：

如何处理这个问题？ 简单做法是：假设我们有一个长度为1000的序列，如果我们设置transformer的最大序列长度是100，那么这个1000长度的序列需要分割成十个固定长度为100的segment，每个片段（segment）之间相互独立，独立处理。这么做的缺点：

• 能建模的依赖关系不会超过segment的长度；
• 会导致context fragmentation（上下文碎片化）：因为分片并不是根据语义边界，而是根据长度划分，很有可能会将一个完整的句子分割，那么在预测一个segment的前几个token的时候，很可能缺乏必要的语义信息。

简单做法问题太多，因此可以借鉴vanilla Transformer中的做法

vanilla Transformer是一个基于原Transformer的character-level的语言模型，仅采用了其Decoder端。我们可以从这个模型中学习如何处理超出定长数据的方法。在训练阶段：vanilla Transformer将输入分成片段，并在每个段中进行学习； 在测试阶段：vanilla Transformer将输入通过滑动的方式分成片段，如需处理较长的输入时，该模型会在每一步中将输入向右移动一个字符，以此实现对单个字符的预测。即每个segment只会向前滑动一个位置，这样速度很慢 如下图所示：

动态图如下：
训练：

预测：

该模型在常用的数据集如enwik8和text8上的表现比RNN模型要好，但它仍有以下缺点：
1.上下文长度受限：字符之间的最大依赖距离受滑动长度的限制，模型看不到出现滑动长度之前的单词。
2.上下文碎片context fragmentation：对于长度超过512个字符的文本，都是从头开始单独训练的。段与段之间没有上下文依赖性，会让训练效率低下，也会影响模型的性能。
3.推理速度慢：在测试阶段，每次预测下一个单词，都需要重新构建一遍上下文，并从头开始计算，这样的计算速度非常慢。

2.2.7.3 transformer XL

2.2.7.3.1 transformer XL的两种改进

目前在NLP领域中，处理语言建模问题有两种最先进的架构：RNN和Transformer。RNN按照序列顺序逐个学习输入的单词或字符之间的关系，而Transformer则接收一整段序列，然后使用self-attention机制来学习它们之间的依赖关系。这两种架构目前来看都取得了令人瞩目的成就，但它们都局限在捕捉长期依赖性上。RNN中是因为随着时间步的加长，靠前的信息对背景变量的影响越来越小；对于Transformer来讲，虽然self-attention不受长度的约束，但是Transformer本身的输入长度是固定的，超出截断，不足补padding。因此Transformer也会受句长的影响。

为了解决这一问题，CMU联合Google Brain在2019年1月推出的一篇新论文《Transformer-XL：Attentive Language Models beyond a Fixed-Length Context》同时结合了RNN序列建模和Transformer自注意力机制的优点，在输入数据的每个段上使用Transformer的注意力模块，并使用循环机制来学习连续段之间的依赖关系。

Transformer-XL架构在vanilla Transformer的基础上引入了两点创新：循环机制（Recurrence Mechanism）和相对位置编码（Relative Positional Encoding），以克服vanilla Transformer的缺点。与vanilla Transformer相比，Transformer-XL的另一个优势是它可以被用于单词级和字符级的语言建模。

1.引入循环机制
与vanilla Transformer的基本思路一样，Transformer-XL仍然是使用分段的方式进行建模，但其与vanilla Transformer的本质不同是在于引入了段与段之间的循环机制，使得当前段在建模的时候能够利用之前段的信息来实现长期依赖性。如下图所示：

在训练阶段，处理后面的段时，每个隐藏层都会接收两个输入：

该段的前面隐藏层的输出，与vanilla Transformer相同（上图的灰色线）。
前面段的隐藏层的输出（上图的绿色线），可以使模型创建长期依赖关系。
这两个输入会被拼接，然后用于计算当前段的Key和Value矩阵。

该方法可以利用前面更多段的信息，测试阶段也可以获得更长的依赖。在测试阶段，与vanilla Transformer相比，其速度也会更快。在vanilla Transformer中，一次只能前进一个step，并且需要重新构建段，并全部从头开始计算；而在Transformer-XL中，每次可以前进一整个段，并利用之前段的数据来预测当前段的输出。

如果采用transformer-xl，首先取第一个段进行计算，然后把得到的结果的隐藏层的值进行缓存，第二个段计算的过程中，把缓存的值拼接起来再进行计算。该机制不但能保留长依赖关系解决上下文碎片问题，还能加快训练，因为每一个前置片段都保留了下来，不需要再重新计算，在transformer-xl的论文中，经过试验其速度比vanilla transformer快了1800倍。

2.相对位置编码

在Transformer中，一个重要的地方在于其考虑了序列的位置信息。在分段的情况下，如果仅仅对于每个段仍直接使用Transformer中的位置编码，即每个不同段在同一个位置上的表示使用相同的位置编码，就会出现问题。比如，第i−2段和第i−1段的第一个位置将具有相同的位置编码，但它们对于第i段的建模重要性显然并不相同（例如第i−2段中的第一个位置重要性可能要低一些）。因此，需要对这种位置进行区分。

论文对于这个问题，提出了一种新的位置编码的方式，即会根据词之间的相对距离编码：也就是说，我们只关心它们是属于同一个Segment还是属于不同的Segment，因为一个token在整个序列中的绝对位置并不重要，只需要在计算attention sorce时知道两个单词的相对位置即可。

在原Transformer中，attention score计算公式如下：
$$\begin{array}{c}{ａ}_{ij}=\frac{\left(x_i{W}^Q\right){\left(x_j{W}^K\right)}^T}{\sqrt{d_z}}=\frac{\left(\left(x_i^{\text{word }}+x_i^{\text{position }}\right)W^Q\right){\left(\left(x_j^{\text{word }}+x_j^{\text{position }}\right)W^K\right)}^T}{\sqrt{d_z}}=\\ \frac{x_i^{\text{word }}{W}_q{W}_k^T{\left(x_j^{\text{word }}\right)}^T+x_i^{\text{word }}{W}_q{W}_k^T{\left(x_j^{\text{position }}\right)}^T+x_i^{\text{position }}{W}_q{W}_k^T{\left(x_j^{\text{word }}\right)}^T+x_i^{\text{position }}{W}_q{W}_k^T{\left(x_j^{\text{position }}\right)}^T}{\sqrt{d_z}}\end{array}$$
将公式中的词向量抽象为 $E_{x_i}$, 位置向量抽象为 $U_j$, 位置编码为绝对位置编码, Transformer的输入为 $E_{x_i}$ 和 $U_j$ 元素和， 因此上述公式可抽象为
$$A_{i,j}^{abs}=E_{x_i}^T{W}_q^T{W}_k{E}_{x_j}+E_{x_i}^T{W}_q^T{W}_k{U}_j+U_i^T{W}_q^T{W}_k{E}_{x_j}+U_i^T{W}_q^T{W}_k{U}_j$$
在Transformer-XL模型中输入输出可抽象为 $h_{\tau +1}=h\left(h_{\tau },E_{s_{\tau }}+U_{1:L}\right),h_{\tau }=h\left(h_{\tau -1},E_{s_{\tau }-1}+U_{1:L}\right),f_{}$ 代表Transformer-XL整个模型函数。其中, $E_{s_{\tau }}\in R^{L\times d}$ 时第 $\tau$ 个序列段 $s_{\tau }$ 的词向量输入，每个序列段的位置向量(Position Embedding)相同。$h_{\tau }$ 代表对于第 $\tau$ 个segment, transformer的输出； $E_{{\mathrm{s}}_{\tau +1}}$ 是第 $\tau +1$ 个segment的初始embedding（输入）; $U_{1:L}$ 代表位置编码。

Transformer-XL中将绝对位置编码转换为相对位置编码，最初的思路是考虑将相对位置编码引入到Attention计算中，对于query vector $q_{\tau ,i}$ 和 key vector $k_{\tau ,\le i}$, 取 $k_{\tau ,j}$ 为例, 只需要考虑两个向量之间的相对位置编码。可以定义一系列相对位置编码 $R\in {\mathbb{R}}^{L_{\max }\times d}$, 在 网络更新过程中，可动态地将相对位置编码加入词向量中。可回顾之前地绝对位置编码地Attention计算公式

$$\begin{array}{rl}{\mathbf{A}}_{i,j}^{\mathrm{a}\mathrm{b}\mathrm{s}}& =\underset{(a)}{\underbrace{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{E}}_{x_j}}}+\underset{(b)}{\underbrace{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{U}}_j}}\\ & +\underset{(c)}{\underbrace{{\mathbf{U}}_i^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{E}}_{x_j}}}+\underset{(d)}{\underbrace{{\mathbf{U}}_i^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{U}}_j}}\end{array}$$
$W_q{E}_{x_i}$ 得到的是第i个token的Query向量, $W_k{E}_{x_j}$ 得到的是第j个token的key向量, $U_i$ 代表 第i个token的位置编码, 所以:

• $a$ 是query向量和 $k$ ey向量的相乘
• b是query向量和key对应的位置编码相乘
• c是query对应位置编码和key向量相乘
• d是query对应位置编码和key对应位置编码相乘

而在transformer-XL中, 做了三处改变:
$$\begin{array}{rl}{\mathbf{A}}_{i,j}^{\mathrm{r}\mathrm{e}\mathrm{l}}& =\underset{(a)}{\underbrace{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_{k,E}{\mathbf{E}}_{x_j}}}+\underset{(b)}{\underbrace{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_{k,R}{\mathbf{R}}_{i-j}}}\\ & +\underset{(c)}{\underbrace{u^{\top }{\mathbf{W}}_{k,E}{\mathbf{E}}_{x_j}}}+\underset{(d)}{\underbrace{v^{\top }{\mathbf{W}}_{k,R}{\mathbf{R}}_{i-j}}}\end{array}$$

• b和d中将Key的绝对位置编码 $U_j$ 改为了相对位置编码 $R_{i-j}，R_{i-j}$ 是一个无需学习的 sinusoidal编码矩阵, 相对的意思是值ｊ相对于ｉ是第几个位置，计算方式同最初的transformer。该方式可以避免不同segments之间由于 tokens在各自segment的index相同而产生的时序冲突的问题。
• ｃ和d中, 将query的绝对位置编码进行了替换，因为query相对于自己的位置是一样, 那么 attention bias的计算与query在序列中的绝对位置无关，应当保持不变
• $W_k\to W_{k,E},W_{k,R}$ 在之前transformer中, token的embedding和position embedding会加起来，再经过 $W_k$ 矩阵做线性变换，即embedding和position encoing是相同的线性变换， 该处改变使得key的embedding和positional encoding 分别采用了不同的线性变换。其中 $W_{k,E}$ 对应于key的embedding线性映射矩阵, $W_{k,R}$ 对应与key的positional encoding的线 性映射矩阵

这样做的好处：

• 解决了在应用了Segment-level Recurrence之后, segment间位置编码冲突的问题
• 可以利用sinusoid 的inductive bias sinusoid并不会受限于序列长度, 即使是训练时从末遇到的序列长度仍能很好的处理, 这也一定程度上体现了inductive bias

2.2.8 GPT

GPT是“Generative Pre-Training”的简称，从名字看其含义是指的生成式的预训练。GPT也采用两阶段过程，第一个阶段是将语言模型进行预训练，第二阶段通过Fine-tuning的模式解决下游任务。

上图展示了GPT的预训练过程，其实和ELMO是类似的，主要不同在于两点：
1.首先，特征抽取器不是用的RNN，而是用的Transformer，上面提到过它的特征抽取能力要强于RNN，这个选择很明显是很明智的；
2.其次，GPT的预训练虽然仍然是以语言模型作为目标任务，但是采用的是单向的语言模型，所谓“单向”的含义是指仅根据被预测单词的上文进行预测。而ELMO在做语言模型预训练的时候，同时使用了被预测单词的上文和下文。这个选择现在看不是个太好的选择，原因很简单，它没有把单词的下文融合进来，这限制了其在更多应用场景的效果，比如阅读理解这种任务，在做任务的时候是可以允许同时看到上文和下文一起做决策的。如果预训练时候不把单词的下文嵌入到Word Embedding中，是很吃亏的，白白丢掉了很多信息。

2.2.9 BERT

2.2.9.1 BERT-base

2.2.9.1.1 介绍

BERT的全称是Bidirectional Encoder Representation from Transformers，是Google2018年提出的预训练模型，即双向Transformer的Encoder（因为decoder是不能获要预测的信息的）。模型的主要创新点都在pre-train方法上，即用了Masked LM和Next Sentence Prediction两种方法分别捕捉词语和句子级别的representation。

那么BERT的创新多吗？并不多，个人感觉提出的两种预训练任务算是创新，那么BERT为什么效果这么好呢？因为BERT算是集大成者，也因为Transformer的Encoder是自编码模型并且采用了预训练-微调的两阶段范式。

为什么预训练可行？

对于层级的CNN结构来说，不同层级的神经元学习到了不同类型的图像特征，由底向上特征形成层级结构，所以预训练好的网络参数，尤其是底层的网络参数抽取出特征跟具体任务越无关，越具备任务的通用性，所以这是为何一般用底层预训练好的参数初始化新任务网络参数的原因。而高层特征跟任务关联较大，实际可以不用使用，或者采用Fine-tuning用新数据集合清洗掉高层无关的特征抽取器。

BERT的模型结构如下（BERT也是两阶段语言模型）：

BERT、GPT、ELMO的区别：
首先看下自回归和自编码语言模型（Language Model）？：
自回归：
在ELMO/BERT之前，大家所讲的语言模型是根据上文内容预测下一个单词，也就是常说的自左向右的语言模型，或者反过来也行，就是根据下文预测前面的单词，这种类型的LM被称为自回归语言模型。GPT 就是典型的自回归语言模型。ELMO尽管看上去利用了上文，也利用了下文，但是本质上仍然是自回归LM（ELMO是两个自回归拼接），这个跟模型具体怎么实现有关系。ELMO是做了两个方向（从左到右以及从右到左两个方向的语言模型），但是是分别有两个方向的自回归LM，然后把LSTM的两个方向的隐节点状态拼接到一起，来体现双向语言模型这个事情的。所以其实是两个自回归语言模型的拼接，本质上仍然是自回归语言模型。

自回归语言模型有优点有缺点：
缺点是只能利用上文或者下文的信息，不能同时利用上文和下文的信息，当然，貌似ELMO这种双向都做，然后拼接看上去能够解决这个问题，因为融合模式过于简单，所以效果其实并不是太好。

优点其实跟下游NLP任务有关，比如生成类NLP任务，比如文本摘要，机器翻译等，在实际生成内容的时候，就是从左向右的，自回归语言模型天然匹配这个过程。而Bert这种DAE模式，在生成类NLP任务中，就面临训练过程和应用过程不一致的问题，导致生成类的NLP任务到目前为止都做不太好。

自编码：
自回归语言模型只能根据上文预测下一个单词，或者反过来，只能根据下文预测前面一个单词。相比而言，Bert通过在输入X中随机Mask掉一部分单词，然后预训练过程的主要任务之一是根据上下文单词来预测这些被Mask掉的单词，如果你对Denoising Autoencoder（降噪自动编码机）比较熟悉的话，会看出，这确实是典型的DAE的思路。那些被Mask掉的单词就是在输入侧加入的所谓噪音，避免过拟合。类似Bert这种预训练模式，被称为DAE LM。

这种DAE LM的优缺点正好和自回归LM反过来，它能比较自然地融入双向语言模型，同时看到被预测单词的上文和下文，使一个字/词可以被上下文很好的表达，这是好处。缺点是啥呢？主要在输入侧引入[Mask]标记，导致预训练阶段和Fine-tuning阶段不一致的问题，因为Fine-tuning阶段是看不到[Mask]标记的。DAE嘛，就要引入噪音，[Mask] 标记就是引入噪音的手段，这个正常。
然后区别：
1.对比GPT，BERT是自编码语言模型，GPT是自回归语言模型。
2.对比ELMo，虽然都是“双向”，但目标函数其实是不同的。ELMo是分别以$P\left(w_i\mid w_1,\dots w_{i-1}\right)$ 和 $P\left(w_i\mid w_{i+1},\dots w_n\right)$ 作为目标函数，独立训练处两个representation然后拼接，而BERT则是以$P\left(w_i\mid w_1,\dots ,w_{i-1},w_{i+1},\dots ,w_n\right)$作为目标函数训练LM。也就是说ELMO是两个自回归拼接成的自编码，而BERT是真正的自编码。

2.2.9.1.2 训练

BERT预训练模型分为以下三个步骤：Embedding、Masked LM、Next Sentence Prediction
1.Embedding
这里的Embedding由三种Embedding求和而成：

Token Embeddings是词向量，第一个单词是CLS标志，可以用于之后的分类任务
Segment Embeddings用来区别两种句子，因为预训练不光做LM还要做以两个句子为输入的分类任务
Position Embeddings和之前文章中的Transformer不一样，不是三角函数而是学习出来的

2.Masked LM
MLM可以理解为完形填空，作者会随机mask每一个句子中15%的词，用其上下文来做预测，例如：my dog is hairy → my dog is [MASK]

此处将hairy进行了mask处理，然后采用非监督学习的方法预测mask位置的词是什么，但是该方法有一个问题，因为是mask15%的词，其数量已经很高了，这样就会导致某些词在fine-tuning阶段从未见过，为了解决这个问题，作者做了如下的处理：

80%是采用[mask]，my dog is hairy → my dog is [MASK]

10%是随机取一个词来代替mask的词，my dog is hairy -> my dog is apple

10%保持不变，my dog is hairy -> my dog is hairy

注意：这里的10%是15%需要mask中的10%

那么为啥要以一定的概率使用随机词呢？这是因为transformer要保持对每个输入token分布式的表征，否则Transformer很可能会记住这个[MASK]就是"hairy"。至于使用随机词带来的负面影响，文章中解释说,所有其他的token(即非"hairy"的token)共享15%*10% = 1.5%的概率，其影响是可以忽略不计的。Transformer全局的可视，又增加了信息的获取，但是不让模型获取全量信息。
3 Next Sentence Prediction
选择一些句子对A与B，其中50%的数据B是A的下一条句子，剩余50%的数据B是语料库中随机选择的，学习其中的相关性，添加这样的预训练的目的是目前很多NLP的任务比如QA和NLI都需要理解两个句子之间的关系，从而能让预训练的模型更好的适应这样的任务。 个人理解：
1.Bert先是用Mask来提高视野范围的信息获取量，增加duplicate再随机Mask，这样跟RNN类方法依次训练预测没什么区别了除了mask不同位置外；
2.全局视野极大地降低了学习的难度，然后再用A+B/C来作为样本，这样每条样本都有50%的概率看到一半左右的噪声；
3.但直接学习Mask A+B/C是没法学习的，因为不知道哪些是噪声，所以又加上next_sentence预测任务，与MLM同时进行训练，这样用next来辅助模型对噪声/非噪声的辨识，用MLM来完成语义的大部分的学习。

2.2.9.1.3 BERT激活函数-GELU

Transformer中用的激活函数还是Relu，而在BERT中用的激活函数是gelu。

基本概念：
概率密度函数
累积分布函数
深度学习模型需要有非线性拟合的能力，这个Relu可以实现，而在训练过程中需要考虑防止过拟合（正则化），这个通过dropout来实现，而zoneout是Dropout的一个变种。而GELU将上面三者的进行了结合，即在激活中加入正则化。

原先的Relu对于输入x，小于0的部分将其置为0，大于0的部分同等映射，总结来讲ReLU会确定性的将输入乘上一个0或者1；再看dropout，dropout是随机乘上0；那么gelu综合以上：同样是将输入像relu一样进行 0/1 mask，但不同的是gelu是以一定的概率输入乘以0/1，而不像relu只要小于0就一定0 mask。

那么gelu中，这个概率怎么来的呢？是通过输入x和具有零均值和单位方差的高斯随机变量X进行比较得到的，GELU激活函数公式如下：（P(X<=x)是X小于或等于给定值x的概率）

$GELU(X)=x\times P(X<=x)=x\times \varphi (x),x\sim N(0,1)$

GELU解释：

ReLU图像：

2.2.9.2 BERT家族

2.2.9.2.1 Roberta

Roberta比起bert有哪些改进？

https://bbs.huaweicloud.com/blogs/145281

https://blog.youkuaiyun.com/ljp1919/article/details/100666563

有以下三方面改进：1.模型的超参；2.模型的训练模式；3.模型的数据

1.模型的超参：
（1）更大batch_size,尝试过从256到8000，当然learning rate随着batch_size增大而增大
（2）优化器Adam参数，原始BERT优化函数采用的是Adam默认的参数，其中(beta_1=0.9, beta_2 = 0.999)，在RoBERTa模型中考虑采用了更大的batches，所以将(beta_2)改为了0.98。
2.模型的训练模式：
（1）去掉下一句预测(NSP)任务：roberta作者经过探索NSP训练策略对模型结果的影响，去掉该训练方式
（2）动态掩码代替静态掩码：原来Bert对每一个序列随机选择15%的Tokens替换成[MASK]，为了消除与下游任务的不匹配，还对这15%的Tokens进行80%的时间替换成[MASK]、10%的时间不变、10%的时间替换成其他词。但整个训练过程，这15%的Tokens一旦被选择就不再改变，也就是说从一开始随机选择了这15%的Tokens，之后的N个epoch里都不再改变了。这就叫做静态Masking；而RoBERTa一开始把预训练的数据复制10份，每一份都随机选择15%的Tokens进行Masking，也就是说，同样的一句话有10种不同的mask方式。然后每份数据都训练N/10个epoch。这就相当于在这N个epoch的训练中，每个序列的被mask的tokens是会变化的。这就叫做动态Masking。以上的Masking指的是广义的mask（替换成[MASK]；保持原词汇；随机替换成另外一个词），并非只局限于单词替换成[MASK]标签的情况。文中epoches = 40（https://blog.youkuaiyun.com/baidu_15113429/article/details/103225548）

3.输入数据：
（1）使用更大的训练集：CC-NEWS 等在内的 160GB 纯文本。而最初的BERT使用16GB BookCorpus数据集和英语维基百科进行训练
（2）文本编码：字节对编码(BPE)(Sennrich et al.,2016)是字符级和单词级表示的混合，该编码方案可以处理自然语言语料库中常见的大量词汇。BPE不依赖于完整的单词，而是依赖于子词(sub-word)单元，这些子词单元是通过对训练语料库进行统计分析而提取的，其词表大小通常在 1万到 10万之间。当对海量多样语料建模时，unicode characters占据了该词表的大部分。Radford et al.(2019、Facebook 研究者)的工作中介绍了一个简单但高效的BPE， 该BPE使用字节对而非unicode characters作为子词单元。：
基于 char-level(BERT) ：它通过对输入文本进行启发式的词干化之后处理得到。
基于 bytes-level(Roberta)：与 char-level 的区别在于bytes-level 使用 bytes 而不是 unicode 字符作为 sub-word 的基本单位，因此可以编码任何输入文本而不会引入 UNKOWN 标记， str2byte代码片段:
str1=‘你’
b=bytes(str1, encoding=‘utf-8’)
print(b)
b’\xe4\xbd\xa0’

2.2.9.2.2 BERT-WWM

Whole Word Masking (wwm)，暂翻译为全词Mask或整词Mask，是谷歌在2019年5月31日发布的一项BERT的升级版本，主要更改了原预训练阶段的训练样本生成策略。 简单来说，原有基于WordPiece的分词方式会把一个完整的词切分成若干个子词，在生成训练样本时，这些被分开的子词会随机被mask。 在全词Mask中，如果一个完整的词的部分WordPiece子词被mask，则同属该词的其他部分也会被mask，即全词Mask。以上的Mask指的是广义的mask（替换成[MASK]；保持原词汇；随机替换成另外一个词），并非只局限于单词替换成[MASK]标签的情况。
比如 super man在原始bert中，可能是super被mask，也可能是man被mask，这样会造成一定的语义割裂，因此在WWM中，只要super 或 man被mask，那么一定是super man都被mask。

2.2.9.2.3 BERT-ENITY

基于BERT-WWM更进一步，因为有些实体是几个词组成的，直接将这个实体都遮盖掉。因此百度在 ERNIE 模型中，就引入命名实体（Named Entity）外部知识，遮盖掉实体单元，进行训练。

2.2.9.2.4 BERT-n-gram mask和random span mask

https://zhuanlan.zhihu.com/p/360982134

2.2.9.3 问答

面经：https://zhuanlan.zhihu.com/p/151412524?ivk_sa=1024320u

2.2.9.3.1 BERT缺点及改进

1.忽略了mask位置词的联系：由于需要 mask 一句话中的部分输入，BERT 忽略了被 mask 位置之间的依赖关系，这点在Roberta中被改进。改进措施如下：

• 动态掩码代替静态掩码：原来Bert对每一个序列随机选择15%的Tokens替换成[MASK]，为了消除与下游任务的不匹配，还对这15%的Tokens进行80%的时间替换成[MASK]、10%的时间不变、10%的时间替换成其他词。但整个训练过程，这15%的Tokens一旦被选择就不再改变，也就是说从一开始随机选择了这15%的Tokens，之后的N个epoch里都不再改变了。这就叫做静态Masking；而RoBERTa一开始把预训练的数据复制10份，每一份都随机选择15%的Tokens进行Masking，也就是说，同样的一句话有10种不同的mask方式。然后每份数据都训练N/10个epoch。这就相当于在这N个epoch的训练中，每个序列的被mask的tokens是会变化的。这就叫做动态Masking。以上的Masking指的是广义的mask（替换成[MASK]；保持原词汇；随机替换成另外一个词），并非只局限于单词替换成[MASK]标签的情况。其实就是通过将数据多次复制进行mask时，可以让原先被mask的位置在复制句里展示。

2.BERT使用的是训练出的绝对位置编码，这种位置编码简单但是限制了输入长度，只有512个，改进措施：

• 换成相对位置编码：华为的NEZHA模型便是一个换成了相对位置编码的BERT模型，但是整个BERT模型得重新预训练。
• 使用transformers中的sin、cos这种绝对位置编码方式就不会受长度限制，但是也得重新训练。
• 层次分解位置编码：具体来说，假设已经训练好的绝对位置编码向量为 ${\mathbf{p}}_1,{\mathbf{p}}_2,\cdots ,{\mathbf{p}}_n$, 我们系望能在此基础上构造一套的编码向量 ${\mathbf{q}}_1,{\mathbf{q}}_2,\cdots ,{\mathbf{q}}_m$, 其中 $m>n$ 。
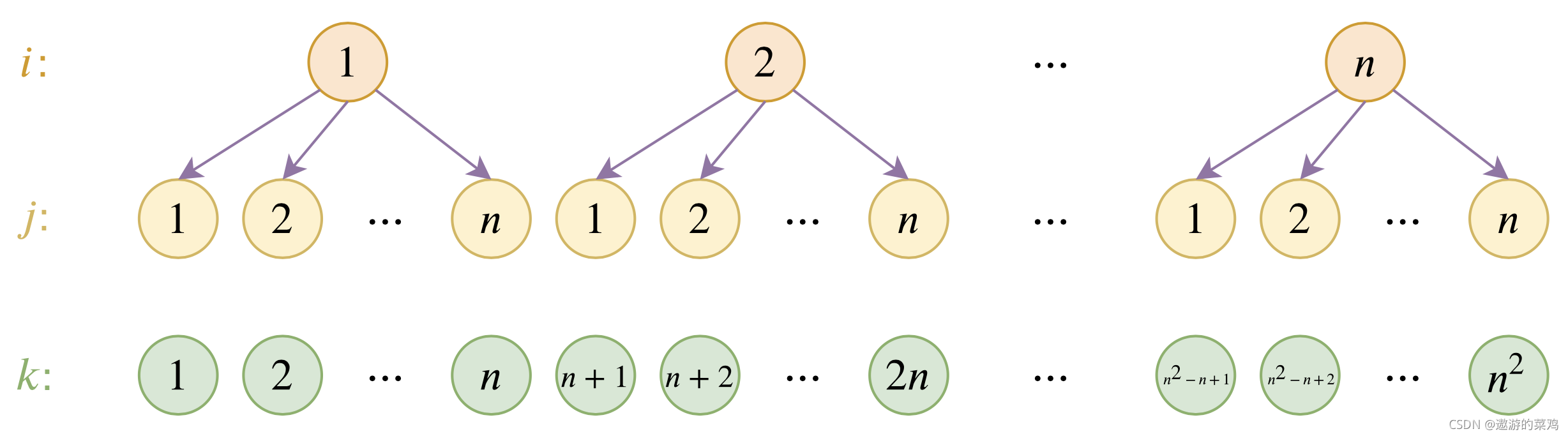
  首先我们可以简单的做一种层次位置编码的处理：假设一共训练了3个位置编码（n=3），那么第一个位置编码q1=p1+p1, q2=p1+p2, q3=p1+p3, q4=p2+p1, q5=p2+p2, q6=p2+p3, q7=p3+p1, q8=p3+p2, q9=p3+p3,这样就能构造$n^2$个新的位置编码了，即第i层第j个位置的的位置编码=i处位置编码+j处位置编码，但是注意上面q6和q8一样，因此这种没法区分（i，j）和（j，i）情况；且q1=p1比q1=p1+p1直观上更好，那么如何区分并解决第一层编码和原始编码不一致的问题呢？只要让(i,j)和(j,i)计算时，加项权重不一致即可，再加上让新位置编码在第一层时和原始编码一致，
  为此，我们设
  $${\mathbf{q}}_{(i-1)\times n+j}=\alpha {\mathbf{u}}_i+(1-\alpha ){\mathbf{u}}_j$$ 很清晰, 就是将位置 $(i-1)\times n+j$ 层次地表示为 $(i,j)$, 然后 $i,j$ 对应的位置编码分别为 $\alpha {\mathbf{u}}_i$ 和 $(1-\alpha ){\mathbf{u}}_j$, 而最终 $(i-1)\times n+j$ 的编码向量则是两者的叠加。要求 $\alpha \ne 0.5$ 是为了区分 $(i,j)$ 和 $(j,i)$ 两种不同的情况。
  我们希望在不超过 $n$ 时 ，位置向量保持跟原来的一样，这样就能与已经训练好的模型兼容。换句话说，我们希望 ${\mathbf{q}}_1={\mathbf{p}}_1,{\mathbf{q}}_2={\mathbf{p}}_2,\cdots ,{\mathbf{q}}_n={\mathbf{p}}_n$, 这样就能反推出各个 ${\mathbf{u}}_i$ 了：
  $${\mathbf{u}}_i=\frac{{\mathbf{p}}_i-\alpha {\mathbf{p}}_1}{1-\alpha },i=1,2,\cdots ,n$$
  这样一来, 我们的参数还是 ${\mathbf{p}}_1,{\mathbf{p}}_2,\cdots ,{\mathbf{p}}_n$, 但我们可以表示出 $n^2$ 个位置的编码，并且前 $n$ 个位罟编码跟原来模型是相容的。
  层次编码图如下：
  

3.预训练和fine-tuning阶段不一致：预训练有【MASK】标记，而fine-tuning阶段却看不到这个标记，解决办法：
XLNet用全排列实现隐式mask。

4.各向异性：BERT词向量训练过程中受词频的影响，导致高频词离原点近且聚集，低频词离原点远且离散，对于语义相似度任务不友好。解决措施：

• bert-flow：On the Sentence Embeddings from Pre-trained Language Models
• bert-whitening：Whitening Sentence Representations for Better Semantics and Faster Retrieval
• 对比学习：SimCSE: Simple Contrastive Learning of Sentence Embeddings
  通过两次dropout构造正负例对，然后通过目标函数实现对比学习，目标函数如下：
  $-{\sum }_{i=1}^N{\sum }_{\alpha =0,1}\log \frac{e^{\cos \left({\mathbf{h}}_i^{(\alpha )},{\mathbf{h}}_i^{(1-\alpha )}\right)/\tau }}{{\sum }_{j=1,j\ne i}^N{e}^{\cos \left({\mathbf{h}}_i^{(\alpha )},{\mathbf{h}}_{ȷ}^{(\alpha )}\right)/\tau }+{\sum }_j^N{e}^{\cos \left({\mathbf{h}}_i^{(\alpha )},{\mathbf{h}}_j^{(1-\alpha )}\right)/\tau }}$

2.2.9.3.2 BERT的损失函数以及两个任务怎样训练

BERT训练有两个任务：MLM、NSP；MLM是mask句子一定数量的单词进行预测，是一个分类问题、NSP是对两句的关系进行预测，也是一个分类问题。

两个任务是同时训练的，同时训练的意思就是把两个任务计算的loss相加同时回传更新，那么MLM和NSP的损失函数是什么？都是负对数似然函数，公式如下（负对数似然函数在多分类问题下和交叉熵损失函数的公式一样，但是说的时候不要说混了）：

那么为什么负对数似然函数在多分类时和交叉熵损失函数一样呢？花书5.5讲了,任何一个负对数似然函数除以样本数,都是变成经验分布的期望,也就是交叉熵
对于一个多分类问题(假设为 $K$ 类), 有数据集 D = { ( x i , y i ) ∣ i } D=\left\{\left(x_{i}, y_{i}\right) \mid i\right\} D={(xi​,yi​)∣i} 。我们希望建立模型去建模 概率分布 $p_{\theta }(y\mid x)$, 模型参数为 $\theta$ 。
我们使用损失函数评估模型的好坏，可以采用两种方式来导出。
极大似然估计
在二分类问题中:
$$p(t\mid x)=(y{)}^t(1-y{)}^{1-t}$$
其中y是模型预测的概率值，t是样本对应的类标签。

那么看看多分类问题，由于是多分类问题, 故样本空间上的 $p(y\mid x)$ 满足某个Categorical distribution。由Categorical distribution定义知,
$$p(y\mid x;p)=\prod _{k=1}^K{p}_k^{y_k}$$
其中， $p$ 是分布的参数，也是分布的输出概率向量。 $y$ 是one-hot编码的标签向量。 例如对于一个天气4分类问题, 输出概率向量如下:
p = {‘rain’: .14, ‘snow’: .37, ‘sleet’: .03, ‘hail’: .46}
则分类为snow的概率为 $\mathrm{Pr}(\mathrm{y}=\mathrm{s}\mathrm{n}\mathrm{o}\mathrm{w}=[0,1,0,0])=.14^0\cdot 37^1.03^0\ast .46^0=0.37$ 我们使用极大似然估计去估计分布参数 $p$ 。
假设有 $n$ 个样本： $\left(x^{(i)},y^{(i)}\right)$, 则似然函数为
$$\mathcal{L}\left(\left(x^{(i)},y^{(i)}\right);p\right)=\prod _{i=1}^n\prod _{k=1}^K{p}_k^{y_k}$$
我们期望最大化似然估计，即最小化负对数似然函数:
$$\min -\sum _{i=1}^n\sum _{k=1}^K{y}_k\log p_k$$
由于采用one-hot编码, 故 $y_k=0$ 的项乘积均为 0 ，只需考虑 $y_k=1$ 时。故上述函数可变形 为:
$$\min -\sum _{i=1}^n\log P_k\left(y_k=1\right)$$
交叉熵
熵的介绍：https://blog.youkuaiyun.com/qq_34405401/article/details/119560028
我们希望能够最小化真实分布 $P(y\mid x)$ 与模型输出分布 $P(\hat{y}\mid x)$ 的距离, 等价于最小化两者的 交叉熵, 其被定义为:
$$-\sum _{y}P(y\mid x)\log Q(\hat{y}\mid x)=-\sum _{k=1}^K{y}_k\log \widehat{y_k}$$
可以说交叉熵是直接衡量两个分布之间的差异，而似然函数则是解释以model的输出为predict对label的解释程度，两者思想不一样，但是最终呈现的形式一样。

2.2.9.3.3 BERT深度、双向体现在哪？为什么要有QKV？为什么要接FFNN

(4) BERT深度双向的特点, 深度体现在哪儿?
答：针对特征提取器, Transformer只用了self-attention，没有使用 RNN、CNN，并且使用了残差连接有效防止了梯度消失的问题，使之可以构建更深层的网络，所以BERT构建了多层深度 Transformer来提高模型性能。
(5) BERT中并行计算体现在哪儿?
答: 不同于RNN计算当前词的特征要依赖于前文计算，有时序这个概念, 是按照时序计算的，而 BERT的Transformer-encoder中的self-attention计算当前词的特征时候, 没有时序这个概念, 是同时利用上下文信息来计算的，一句话的token特征是通过矩阵并行瞬间 完成运算的，故，并行就体现在self-attention的计算以及mutli-head。
(6) BERT中Transformer中的Q、K、V存在的意义?
答：在使用self-attention通过上下文词语计算当前词特征的时候，X先通过WQ、WK、WV线性变换为QKV， 然后如下式右边部分使用QK计算得分，最后与V计算加权和而得。
$$\text{ Attention }(Q,K,V)=\mathrm{sottmax}\left(\frac{Q{K}^T}{\sqrt{a^{\top }k}}\right)V$$
倘若不变换为QKV，直接使用每个token的向量表示点积计算重要性得分，那在softmax后的加权平均中，该词本身所占的比重将会是最大的，使得其他词的比重很少，无法有效利用上下文信息来 增强当前词的语义表示。而变换为QKV再进行计算，能有效利用上下文信息，很大程度上减轻上述的影响。
(7) BERT中Transformer中Self-attention后为什么要加前馈网络?
答：1.由于self-attention中的计算都是线性了，因此通过FFNN中的激活函数增加非线性能力（这个说法不准确，增加非线性能力的是激活函数，而如果只为了增加非线性能力可以只增加激活函数）；2.降维，经过mutli-head后数据特征的维度已经是多头相加了，为了保证下个Encoder的输入维度一样，这里进行降维（这个也不太准确，当Q、K、V维度*mutli head数目=Embedding维度时就不用降维了）。

2.2.10 XLNet

2.2.10.1 XLNet介绍

XLNet 是一个类似 BERT 的模型，而不是完全不同的模型。总之，XLNet是一种通用的自回归预训练方法，在论文中是以Transformer为基础实现的。它是CMU和Google Brain团队在2019年6月份发布的模型，最终，XLNet 在 20 个任务上超过了 BERT 的表现，并在 18 个任务上取得了当前最佳效果（打不过Roberta），包括机器问答、自然语言推断、情感分析和文档排序。

作者表示，BERT 这样基于去噪自编码器的预训练模型可以很好地建模双向语境信息，性能优于基于自回归语言模型的预训练方法。然而，由于需要 mask 一部分输入，BERT 忽略了被 mask 的单词之间的依赖关系，并且mask并没有在微调阶段出现，因此可能出现预训练和微调效果的差异（pretrain-finetune discrepancy）。

基于这些优缺点，该研究提出了一种泛化的自回归预训练模型 XLNet。XLNet 可以：

• 通过最大化所有可能的排列解顺序的对数似然，学习双向语境信息；
• 用自回归本身的特点克服 BERT 的缺点；
• 此外，XLNet 还融合了当前最优自回归模型 Transformer-XL 的思路。

2.2.10.2 XLNet做法

XLNet是排列语言建模（Permutation Language Modeling），为了解决上文提到的问题, 作者提出了排列语言模型，该模型不再对传统的AR模型的序列的值按顺序进行建模, 而是最大化所有可能的序列的排列顺序的期望对数似然, 这句话可能有点不好理解, 我们以一个例子来详细说明，假如我们有一个序列 $[1,2,3,4]$, 如果我们 的预测目标是 3, 对于传统的AR模型来说，结果是 $p(3)={\prod }_{t=1}^{3}p\left(3\mid x_{<t}\right)$, 如果采用本文的方法, 先对该序列进行因式分解，最终会有 24种排列方式, 下图是其中可能的四种情况，对于第一种情况因为 3 的左边没有其他的值, 所以该情况无需做对应的计算, 第二种情况3 的左边还包括了2与 4, 所以得到的结果是 $p(3)=p(3\mid 2)\ast p(3\mid 2,4)$, 后续的情况类似，聪明的你一定发现了, 这样处理过后不但保留 了序列的上下文信息，也避免了采用mask标记位, 巧妙的改进了bert与传统AR模型的缺点。

此时，需要强调一点，尽管上面讲的是把句子X的单词排列组合后，再随机抽取例子作为输入，但是，实际上你是不能这么做的，因为Fine-tuning阶段你不可能也去排列组合原始输入。所以，为了保持训练和预测阶段一直，就必须让预训练阶段的输入部分，看上去仍然是x1,x2,x3,x4这个输入顺序，然后可以在Transformer部分做些工作，来达成我们希望的目标。当然，预测时内部不需要进行处理。

具体而言，XLNet采取了Attention掩码的机制，你可以理解为，当前的输入句子是X，要预测的单词Ti是第i个单词，前面1到i-1个单词，在输入部分观察，并没发生变化，该是谁还是谁。但是在Transformer内部，通过Attention掩码，从X的输入单词里面，也就是Ti的上文和下文单词中，随机选择i-1个，放到Ti的上文位置中，把其它单词的输入通过Attention掩码隐藏掉，于是就能够达成我们期望的目标（当然这个所谓放到Ti的上文位置，只是一种形象的说法，其实在内部，就是通过Attention Mask，把其它没有被选到的单词Mask掉，不让它们在预测单词Ti的时候发生作用，如此而已。看着就类似于把这些被选中的单词放到了上文Context_before的位置了）。

这样做会有问题，因为没有考虑位置关系，因此不同排列最后的计算结果是一致的，比如1，2，3序列， 预测3时，如果没有考虑1和2的位置关系，那么对于Transformer来讲，1，2预测3，和2，1预测3是一样的，因此需要考虑位置编码。
具体实现的时候，XLNet是用“双流自注意力模型”实现的。双流自注意力模型： 一个是内容流自注意力，其实就是标准的Transformer的计算过程：self-attention；另一个是Query流自注意力，这个是干嘛的呢？其实就是用来代替Bert的那个[Mask]标记的，因为XLNet希望抛掉[Mask]标记符号，但是比如知道上文单词x1,x2，要预测单词x3，此时在x3对应位置的Transformer最高层去预测这个单词，但是输入侧不能看到要预测的单词x3，Bert其实是直接引入[Mask]标记来覆盖掉单词x3的内容的，等于说[Mask]是个通用的占位符号。而XLNet因为要抛掉[Mask]标记，但是又不能看到x3的输入，于是Query流，就直接忽略掉x3输入了，只保留这个位置信息，用参数w来代表位置的embedding编码。其实XLNet只是扔了表面的[Mask]占位符号，内部还是引入Query流来忽略掉被Mask的这个单词。和Bert比，只是实现方式不同而已。

内容流自注意力如下：

query自注意力如下（该表述包含上下文的内容信息以及位置信息，而目标词只包含了位置信息，从图中可以看到，K与V的计算并没有包括Q，自然也就无法获取到目标的内容信息，但是目标的位置信息在计算Q的时候保留了下来）：

self-attention的计算过程中两个流的网络权重是共享的，最后在微调阶段，只需要简单的把query stream移除，只采用content stream即可。

2.2.10.3 XLNet与BERT比较

尽管看上去，XLNet在预训练机制引入的Permutation Language Model这种新的预训练目标，和Bert采用Mask标记这种方式，有很大不同。其实你深入思考一下，会发现，两者本质是类似的。

区别主要在于：

• Bert是直接在输入端显示地通过引入Mask标记，在输入侧隐藏掉一部分单词，让这些单词在预测的时候不发挥作用，要求利用上下文中其它单词去预测某个被Mask掉的单词；
• 而XLNet则抛弃掉输入侧的Mask标记，通过Attention Mask机制，在Transformer内部随机Mask掉一部分单词（这个被Mask掉的单词比例跟当前单词在句子中的位置有关系，位置越靠前，被Mask掉的比例越高，位置越靠后，被Mask掉的比例越低），让这些被Mask掉的单词在预测某个单词的时候不发生作用。

所以，本质上两者并没什么太大的不同，只是Mask的位置，Bert更表面化一些，XLNet则把这个过程隐藏在了Transformer内部而已。这样，就可以抛掉表面的[Mask]标记，解决它所说的预训练里带有[Mask]标记导致的和Fine-tuning过程不一致的问题。至于说XLNet说的，Bert里面被Mask掉单词的相互独立问题，也就是说，在预测某个被Mask单词的时候，其它被Mask单词不起作用，这个问题，你深入思考一下，其实是不重要的，因为XLNet在内部Attention Mask的时候，也会Mask掉一定比例的上下文单词，只要有一部分被Mask掉的单词，其实就面临这个问题。而如果训练数据足够大，其实不靠当前这个例子，靠其它例子，也能弥补被Mask单词直接的相互关系问题，因为总有其它例子能够学会这些单词的相互依赖关系。

当然，XLNet这种改造，维持了表面看上去的自回归语言模型的从左向右的模式，这个Bert做不到，这个有明显的好处，就是对于生成类的任务，能够在维持表面从左向右的生成过程前提下，模型里隐含了上下文的信息。所以看上去，XLNet貌似应该对于生成类型的NLP任务，会比Bert有明显优势。另外，因为XLNet还引入了Transformer XL的机制，所以对于长文档输入类型的NLP任务，也会比Bert有明显优势。

参考文献

提纲：
https://github.com/NLP-LOVE/ML-NLP
n-gram：
https://zhuanlan.zhihu.com/p/32829048
https://www.jianshu.com/p/c13b9468a924
https://www.jianshu.com/p/c13b9468a924
https://zhuanlan.zhihu.com/p/96826160
https://blog.youkuaiyun.com/tianyouououou/article/details/95591532
word2vec：
https://www.cnblogs.com/pinard/p/7160330.html
https://www.cnblogs.com/pinard/p/7243513.html
https://www.cnblogs.com/pinard/p/7249903.html
Transformer：
https://blog.youkuaiyun.com/Tw6cy6uKyDea86Z/article/details/109505208
https://www.zhihu.com/question/357893845/answer/1885329756
https://zhuanlan.zhihu.com/p/121662739
https://zhuanlan.zhihu.com/p/266463801
https://blog.youkuaiyun.com/u012526436/article/details/93196139
https://blog.youkuaiyun.com/weixin_37947156/article/details/93035607
https://blog.youkuaiyun.com/weixin_42137700/article/details/106616447
https://zhuanlan.zhihu.com/p/142380694
Transformer-decoder：
https://zhuanlan.zhihu.com/p/121662739
https://www.cnblogs.com/wangliman/p/10913735.html
Vanilla Transformer：
https://zhuanlan.zhihu.com/p/85612521
https://blog.youkuaiyun.com/u010366748/article/details/114301942
https://blog.youkuaiyun.com/pingpingsunny/article/details/105056297
Transformer-XL:
https://zhuanlan.zhihu.com/p/85612521
Transformers位置编码
https://blog.youkuaiyun.com/smilesooo/article/details/106224377
https://dengbocong.blog.youkuaiyun.com/article/details/107939242
BERT：
https://blog.youkuaiyun.com/weixin_37947156/article/details/99235621
https://zhuanlan.zhihu.com/p/360982134
BERT-损失函数
https://www.zhihu.com/question/328123545
https://zhuanlan.zhihu.com/p/165139520
https://blog.youkuaiyun.com/qq_38469553/article/details/83860335
BERT-深度、双向、QKV、FFNN？
https://zhuanlan.zhihu.com/p/195723105
XLNet：
https://blog.youkuaiyun.com/u012526436/article/details/93196139
GELU：
https://zhuanlan.zhihu.com/p/302394523
https://zhuanlan.zhihu.com/p/349492378
scaled dot-product attention：
https://zhuanlan.zhihu.com/p/151412524?ivk_sa=1024320u
https://www.zhihu.com/question/339723385/answer/782509914