C++STL详解五：红黑树和关联容器

系列文章目录

---

前言

关联式容器没有顺序容器那么百家齐放，STL中之定义了两种关联式容器：set和map。这两种关联式容器的底层均是使用红黑树去进行实现的，或者说这两个关联式容器更像是对红黑树外加的适配器。由set和map延伸出来的还有multiset和multimap，与set和map不同的是，这两个可以存在重复的键值。

这里，由于无序容器和关联容器的行为相同，我就不在对于无序容器另作介绍了。无需容器和关联容器的差别在于底层实现，无序容器采用hash_table，而关联容器采用红黑树。 hash_table比较简单，我这里主要讲红黑树。

在下边我会实现这两个容器底层的红黑树，至于容器本身，我只介绍他们的行为和区别。

---

一、红黑树(RB-tree)

1.什么是红黑树

红黑树是一种特殊的二叉搜索树，它需要服从以下规则：

1. 每个节点不是红色就是黑色
2. 根节点为黑色
3. 如果节点为红色，其子节点必须为黑色
4. 任意节点至NULL（树的尾端）的任何路径中，所含黑节点数必须相同

在讨论时，将空节点NULL视为黑色，可以大幅度降低复杂度

根据规则4，新增节点必须为红色；根据规则三，新增节点的父节点必须为黑色。若我们插入一个节点通过二叉搜索树的规则找到了插入点但是并不满足上述条件，就必须调整颜色或改变树形，如下图：

我们需要注意的是叶子节点不一定都要是红色，在调整之后也可以是黑色。但在插入时需要是红色。这里插入3时，根据二叉搜索树的条件，确实需要在这个位置插入3，但是插入之后却并不满足红黑树的条件。此时就需要对树形进行改变。

2.红黑树的旋转

旋转分为单旋转和双旋转，单旋转一般用于外侧插入后的失衡，双旋转一般用于内侧插入之后的失衡。
内侧插入和外侧插入如下图：
单旋转分为左旋转和右旋转：
左旋转：以某个结点作为支点(图中为A)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变。
右旋转：以某个结点作为支点(图中为A)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变。

注：图中节点的红黑并非节点属性，只是用来区分新加节点和原有节点

双旋转则是进行两次单旋转，有可能是先左后右，也可能是先右后左，如下图：

注：图中节点的红黑并非节点属性，只是用来区分新加节点和原有节点

3.红黑树的插入操作

下边我们看二叉树的插入时的几种情况：
为了方便描述，我先为将会用到的节点起几个名字：
新增节点：X
新增节点父节点：P
新增节点的祖父节点：G 曾祖父节点：GG
父节点的兄弟节点：S

情况1：S为黑且X为外侧插入。此时我们先对P、G做一次单旋转，然后改变颜色就可以满足规则，如下图：
这里进行旋转式因为节点G不满足二叉搜索树的条件：两子树的深度相差不能大于1
进行变色是因为P节点不满足红黑树的条件：红色节点的子节点为黑色

情况2：S为黑且X为内侧插入。此时我们必须先对P、X做一次单旋转并改变G、X的颜色，再将结果对G做一次单旋转。如下图：
通过第一次旋转可以将这种情况变成上一种的外侧插入，然后根据情况一的方法在进行调整。

情况3：S为红且X为外侧插入。此时先对P和G做一次单旋转并改变X的颜色。若此时GG为黑则万事大吉直接结束，若GG为红，则见下一种情况。如图：
这里不能只改变颜色，若只改变颜色的话，G左子树的黑节点就比右子树多了，所以需要先进行旋转再改变颜色。此时若GG为黑色则满足条件，若GG为红，则又会违反规则3，我们下面再介绍这种情况。

情况4：S为红且X为外侧插入。此时先对P和G做一次单旋转并改变X的颜色。若此时GG也为红色，则需要继续向上进行，直到不再有父子连续为红色的情况为止，如下图：

为了避这种情况的发生，我们可以采用一个自上而下的程序。假设新增节点为A，那么就沿着A的路径，只要看到有某个节点X的两根子节点都为红色，那么就吧X改为红色，并且把他的两个子节点都改成黑色。如下图：

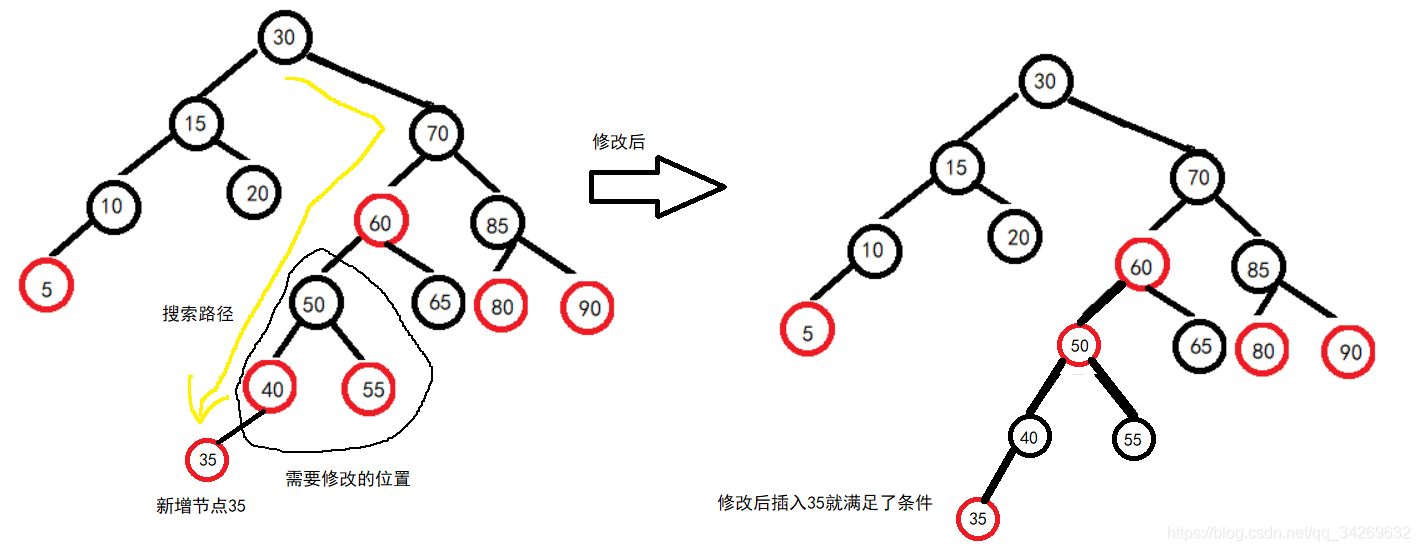
做完这个动作后再次进行插入操作，就会类似于上边的三种情况了。

二、关联式容器底层红黑树的实现

1.红黑树节点的定义

我先把基层节点的定义放出来

//全局的定义，用来储存红黑树的颜色属性
typedef bool color_type;//红黑树颜色的变量类型
const color_type red = false;//红色为0
const color_type black = true;//黑色为1

//红黑树节点的 基层节点
struct _rb_tree_node_base
{
   
	typedef _rb_tree_node_base*  base_ptr;
	
	_rb_tree_node_base()//构造函数
		:color(false), parent(nullptr), left(nullptr), right(nullptr) 
	{
   };

	color_type color;//节点的颜色
	base_ptr parent;//父节点
	base_ptr left;//左子树
	base_ptr right;//右子树

	//寻找最小值，由于二叉搜索树的最小值永远在左边，所以一直向左走就行
	static base_ptr minimum(base_ptr x) {
   
		while(x->left != nullptr)
			x = x->left;
		return x;
	}
	//寻找最大值，由于二叉搜索树的最大值永远在右边，所以一直向右走就行
	static base_ptr maximum(base_ptr x) {
   
		while(x->right != nullptr)
			x = x->right;
		return x;
	}
};

这里并没有定义它的数值域，只是定义了指针域，所以到这里，节点的形式应该如下图：

而红黑树真正的节点，为这个基层节点增加了一个数值域，定义如下

//红黑树的节点
template<class value>
struct _rb_tree_node : public _rb_tree_node_base
{
   //继承自基层节点
	typedef _rb_tree_node<value>* link_type;
	_rb_tree_node(value x = 0) : value_field(x) {
   };
	value value_field;//数值域
};

这里的value采用模板参数，因为这个红黑树将来需要为容器进行服务，容器的元素并不是给定的。对于set来说，这个value既是数值也是键值，对于map来说，这应该是个由数值和键值组成的pair。

2.红黑树的迭代器

由于红黑树是树形结构，他在内存中肯定不是顺序存储的，所以我们的迭代器在设计时就有必要使++操作可以按照一定的顺序遍历整个树，这个顺序在STL的红黑树中是按照键值的从小到大。最小值的位置设置为begin()，根节之上的空节点(在下边主类的实现中会提到)设置为end()。

先来看红黑树迭代器的基类：

//红黑树迭代器的 基层节点
struct _rb_tree_iterator_base
{
   
	typedef _rb_tree_node_base::base_ptr base_ptr;
	typedef ptrdiff_t difference_type;

	//指向红黑树的一个节点
	base_ptr node;

	void increment()
	{
   //移动到下一个更大的节点
		if (node->right != nullptr) {
   //若当前节点存在右子树
			node = node->right;//从节点的右子树开始寻找
			while (node->left != nullptr)//找到右子树的最左节点
				node = node->left;
		}
		else//若没有右子节点
		{
   
			base_ptr y = node->parent;//找出父节点
			while (node == y->right)//若当前node是它父节点的右子节点
			{
   //一直上移，直到当前node是它父节点的左子节点
				node = y;
				y = y->parent;
			}
			if (node->right != y)//若此时node的右子节点等于他的父节点，则父节点为解答
				node = y;		//否则node为解答
		}
	}
	void decrement()
	{
   //移动到上一个更小的节点
		if (node->color == red && node->parent->parent == node)//如果是根节点或end（）时
			node = node->right;
		else if (node->left != 0)//若当前节点存在左子树
		{
   
			base_ptr y = node->left;//从左子树开始
			while (y->right != nullptr)//找到他的最右子树
				y = y->right;
			node = y;
		}
		else//既不是根节点，也没有左子树
		{
   
			base_ptr y = node->parent;//从父节点开始
			while (node == y->left)//直到当前节点node不是它父节点的左子节点
			{
   
				node = y;
				y = y->parent;
			}
			node = y;//此时的父节点就是解答
		}
	}
};

这里使用一个指向红黑树基层节点的指针作为迭代器和容器之间的联系，并且实现了两个函数：increment()和decrement()，这两个函数的作用是将当前的迭代器移动到下一个更大(或上一个更小)的节点，这是为了让迭代器重载++和- -的操作符使用。这个两个函数利用了红黑树主类中的一种定义，我会在下边提及，这里先去看迭代器主类的定义：

//红黑树的迭代器
template<class value>
struct _rb_tree_iterator : public _rb_tree_iterator_base
{
   //继承自基层迭代器
	//定义型别
	typedef value value_type;
	typedef value& reference;