C++ 红黑树、关联式容器map、set

在很久之前我们说过AVL树，其是一种完全平衡的二叉搜索树。这篇文章我们将介绍另一种也是我们比较常用的二叉搜索树：

红黑树

红黑树是在二叉树的基础上，给结点增加了两种颜色（红，黑），以及通过其特定的性质来保证：树中最长路径的的结点个数不会超过最短路径结点个数的两倍。因此红黑树是一个近似平衡的二叉搜索树。
因此红黑是是一个仅此平衡的二叉搜索树。其时间复杂度为O(lgN)，与AVL树相同。但是大量证明表示红黑树的性质远好于AVL树。

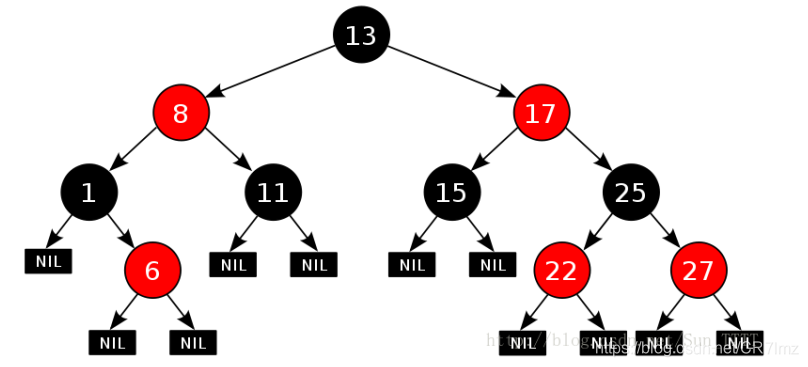
先来看看红黑树的特性：
1.每个结点不是红色就是黑色。
2.根结点必须是黑色。
3.不能有相邻的两个结点颜色都是红的。
4.从某个结点到叶子的每条路径中黑色结点个数必须相同。
5.每一个叶子结点都是黑的（指的是叶子结点的下一个空位置，如图null处）。

红黑树结点定义

enum color {RED , BLACK};

template <class T>
struct RBTreeNode
{
	RBTreeNode(const T& x = T())
		: val(x)
		, clr(RED)
		, pLeft(nullptr)
		, pRight(nullptr)
		, pParent(nullptr)
	{}
	T val;
	color clr;
	struct RBTreeNode<T>* pLeft;
	struct RBTreeNode<T>* pRight;
	struct RBTreeNode<T>* pParent;
};

那么大家也许会有疑问为什么将红黑树的结点默认初始化为红色，而不是黑色呢？
实际上两个颜色都是可以的，因此我们要根据用哪个颜色对红黑树影响小，来选择。
举个例子：
如果我们选择用黑色，有这么一个场景：树中只有插入了一个结点，此时我
们再插入新的结点，那么就一定会违背前面的性质4。
如果我们选红色，用上面那个场景来说，满足性质4。虽然在其他场景下，有可能影响性质3，但是比选黑色对红黑树的影响小。
因此选红色。

红黑树完整的图：

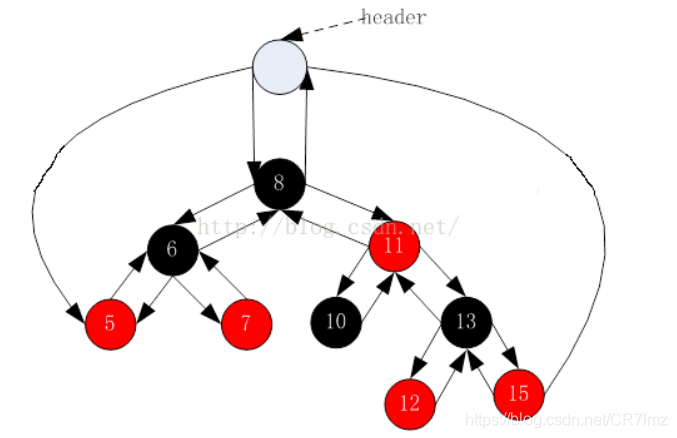
这里有个header结点是为了之后封装map以及set更方便些，header的父亲指针域指向根结点，header的左指针域指向树中最小的结点，header的右指针域指向树中最大的结点。

红黑树的插入操作：
红黑树的插入新结点的的操作，与二叉搜索树的插入操作相同，此处不再赘述。此处主要是看看插入新结点后，红黑树的性质是否遭到破坏，如果遭到破坏就要对其进行调整。

当我们插入结点的父节点颜色为红色，就违反了性质3，因此就要对齐进行调整。此处要分为三者种情况：
我们规定cur为新插入结点，p为父节点，c为叔叔结点，g为爷爷结点。

第一种情况：cur、p为红色，g为黑色，c存在为红色。

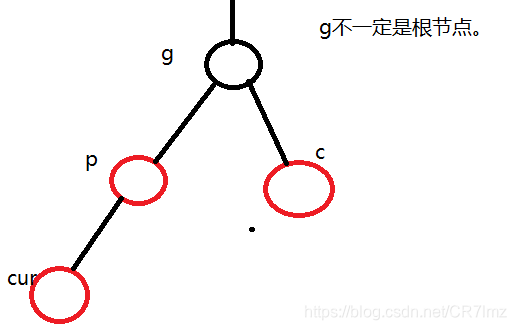
此时违背了性质3，所以我们将p或cur其中一个置为黑色即可，但是此时就违背了性质4，因此将c也置为黑色。此时有两种情况：(1)如果g为根节点那么调整完成。(2)如果g不为根节点，那么g的父节点的左右路径黑色节点数就不一样了，违反了性质4。因此我们将g置为红色即可。此时就满足了红黑树的所有性质。因为我们将g置为红色了，有可能造成上一层违背了红黑树性质，因此继续向上去调整，将cur指向g处，p为cur的父节点。
此时就会出现一个问题，如果最开始我们规定将cur置为黑色，那如果向上一层也需要调整，按照之前的方法将cur置为黑色，也就是将上图p又置为黑色了，就会造成破坏已经调整好的颜色。因此我们规定将p置为黑色即可。

第二种情况：cur、p为红色，g为黑色，c不存在或存在为黑色。

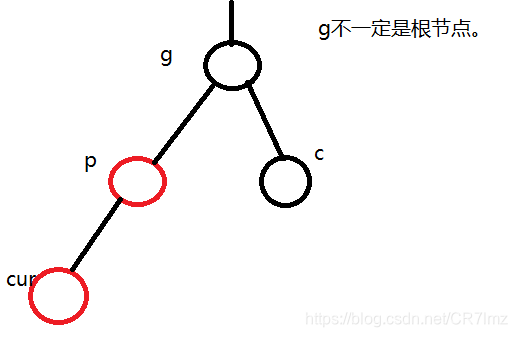
此时违背了性质3、4。我们将p置为黑色，满足了性质3、4，但是此时g的父节点的左右路径中黑色结点数就不一样了，因此与情况一相同，将g置为红色，但是之前gc这条路径上黑色节点个数为2，此时为1个，相当于少了一个结点也是不行的，因此进行右旋操作即可解决，自此调整结束。
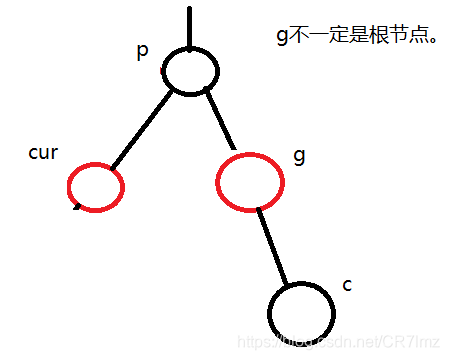因为此时p为黑色，所以不影响上层树，不用继续向上调整。

第二种情况：cur、p为红色，g为黑色，c不存在或存在为黑色。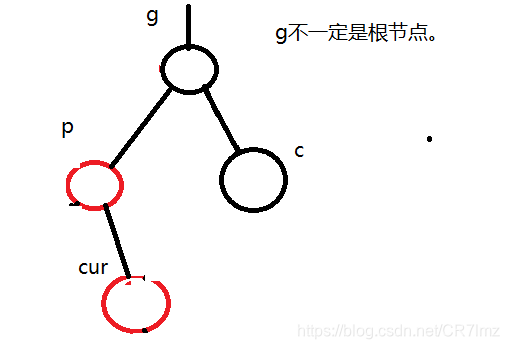
我们可以发现情况3和情况2类似，因此我们只需要将情况3变为情况而即可，之后操作相同。只需要以p为根节点对其进行左旋操作，交换p、cur的指向，即可。

上述讲述三种情况讲述的是p为g的左子树，c为g的右子树这种结构下。另一种结构就不在多说了。

红黑树和AVL树的异同：
相同处：
1.都是高效的平衡二叉树搜索树。
2.增删查改的时间复杂度都是O(lgN)。
不同处：
1.AVL树是绝对的平衡，但是红黑树不是绝对的平衡。
2.红黑树对于降低了插入和旋转的次数，所以一般比AVL性能更好。实际运用中红黑树更多。

map、set

map和set是STL标准库中的关联式容器，其底层用的就是红黑树实现的，因此他们都是树形结构的关联式容器。
注意的是：
map：
存储的是K-V键值对。
set：
存储的是K值。

map/set异同：
相同点：
1.STL标准库中关联式容器。
2.进行中序遍历都是有序序列。
3.查询时间复杂度为：O(lgN)
4.都是用红黑树实现的。
5.迭代器运动方式都是按照中序遍历进行运动的。
不同点：
map：存储的是K-V键值对，并且K-V键值对唯一，按照K进行排序和去重。
多了一个根据K去找V的操作（operator）
set:存储的是K值，并且K-V键值对唯一，按照K进行排序和去重。