【深度学习基础】第七课：激活函数

【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。

1.前言

目前为止，我们所用的激活函数都是sigmoid函数，但有时其他函数的效果要更好，本文将介绍其他常用的激活函数。

2.常用的激活函数

2.1.tanh函数

tanh函数又叫双曲正切函数：

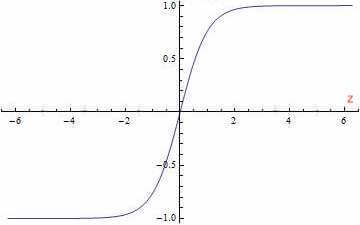
有：

$$a=g(z)=\tanh (z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$

a表示activate function，即激活函数。

可以看出，tanh函数其实就是sigmoid函数平移后的版本。

⚠️tanh函数作为激活函数的效果几乎总是比sigmoid函数的效果要好！但是有一个例外：如果输出的结果为二分类问题，则输出层可以选择sigmoid函数作为激活函数。

❗️不同层的激活函数可以不同。例如我们可以用$g^{[1]}(z^{[1]})$表示第一层的激活函数，用$g^{[2]}(z^{[2]})$表示第二层的激活函数。

⚠️但是tanh函数和sigmoid函数都存在一个很明显的缺点：当z值很大或者很小的时候，函数的斜率就会变得非常小（接近于0），这样会拖慢梯度下降算法。

2.2.ReLU函数

ReLU函数(Rectified Linear Unit, ReLU)，又称修正线性单元：

公式为：$a=g(z)=max(0,z)$。

• 当z为负时，斜率为0。
• z刚好为0时，导数是不存在的。但是在实际情况中，z=0的概率非常非常低。所以在编程实现时，并不需要考虑这个问题。或者也可以当z=0时，把导数值设为0或1。
• 当z为正时，斜率为1。

‼️ReLU函数是大多数神经网络的默认激活函数。因此在不知道选择哪种函数作为激活函数时，可以优先选择ReLU函数。

⚠️ReLU函数的一个缺点就是当z<0时，导数为0。因此引入Leaky ReLU函数克服这个缺点。

2.3.Leaky ReLU函数

Leaky ReLU函数的图像见下：

公式可能为：$a=g(z)=max(0.01z,z)$。常数通常为0.01，当然也可以作为一个参数，从而根据实际情况进行调整。

⚠️Leaky ReLU的效果通常比ReLU函数要好，但是实际使用的频率并不高。

❗️ReLU函数（或Leaky ReLU函数）不会因为z值过大而导致学习速度减慢，因此以ReLU函数（或Leaky ReLU函数）作为激活函数的神经网络的学习速度通常比sigmoid函数和tanh函数快很多。

3.激活函数的选择

可以通过交叉验证的方法选择最适合的激活函数。

4.为什么需要非线性激活函数

从上述介绍可以看出，基本所有的激活函数都是非线性函数。那么神经网络为什么需要这些非线性激活函数呢？

正常的神经网络结构见下：

$g^{[1]}$和$g^{[2]}$为非线性激活函数，我们现在将其改为线性激活函数（也称恒等激活函数）：

• $$a^{[1]}=z^{[1]}=W^{[1]}x+b^{[1]}\text{\hspace{1em}(4.1)}$$
• $$a^{[2]}=z^{[2]}=W^{[2]}{a}^{[1]}+b^{[2]}\text{\hspace{1em}(4.2)}$$

将式4.1带入式4.2：

$$\begin{array}{rl}{a}^{[2]}& =W^{[2]}(W^{[1]}x+b^{[1]})+b^{[2]}\\ & =(W^{[2]}{W}^{[1]})x+(W^{[2]}{b}^{[1]}+b^{[2]})\\ & =W^{\prime }x+b^{\prime }\end{array}$$

⚠️可以看出，假设我们使用线性激活函数，那么神经网络的输出其实就是输入特征的线性组合。这种情况下，隐藏层就失去了存在的意义。

❗️只有一个地方可以使用线性激活函数：当解决回归问题时，输出层的激活函数可以为线性激活函数。

5.激活函数的导数

当进行反向传播时就需要计算激活函数的导数。

1. sigmoid函数：$g^{\prime }(z)=\frac{d}{dz}g(z)=g(z)(1-g(z))=a(1-a)$。
2. tanh函数：$g^{\prime }(z)=1-a^2$。
3. ReLU函数：
   • $ifz<0,g^{\prime }(z)=0$。
   • $ifz>0,g^{\prime }(z)=1$。
   • $ifz=0,undefined$。但是在实际编码中，可令$g^{\prime }(z)=1or0$（原因见2.2部分）。
4. Leaky ReLU函数：
   • $ifz<0,g^{\prime }(z)=0.01$（以2.3部分的公式为例）。
   • $ifz>0,g^{\prime }(z)=1$。
   • 同理，当z=0时，可令$g^{\prime }(z)=1or0.01$。

---

想要获取最新文章推送或者私聊谈人生，请关注我的个人微信公众号：⬇️x-jeff的AI工坊⬇️

个人博客网站：https://shichaoxin.com

GitHub：https://github.com/x-jeff

---