【数学基础】第二课：目标函数、损失函数、代价函数

1.目标函数、损失函数、代价函数

关于损失函数（loss function）、代价函数（cost function）的概念有两种看法：

• 观点一：可认为是一样的。
• 观点二：
  1. 损失函数$\mid y_i-f(x_i)\mid$，一般针对单个个体。
  2. 代价函数$\frac{1}{N}{\sum }_{i=1}^N\mid y_i-f(x_i)\mid$，一般针对总体。

目标函数：$\frac{1}{N}{\sum }_{i=1}^N\mid y_i-f(x_i)\mid +\lambda J(f)$。其中，$J(f)$为正则化项。

上述式子中，$y_i$是真实值，$f(x_i)$是预测值，$N$是样本数。

实际上，这些概念的定义并没有一个统一的说法，这里只是给出一种比较常见的定义。其实只要理解了背后的公式，可根据上下文语境自行判断，叫法并不重要。

2.经验风险和结构风险

先来看一个例子：

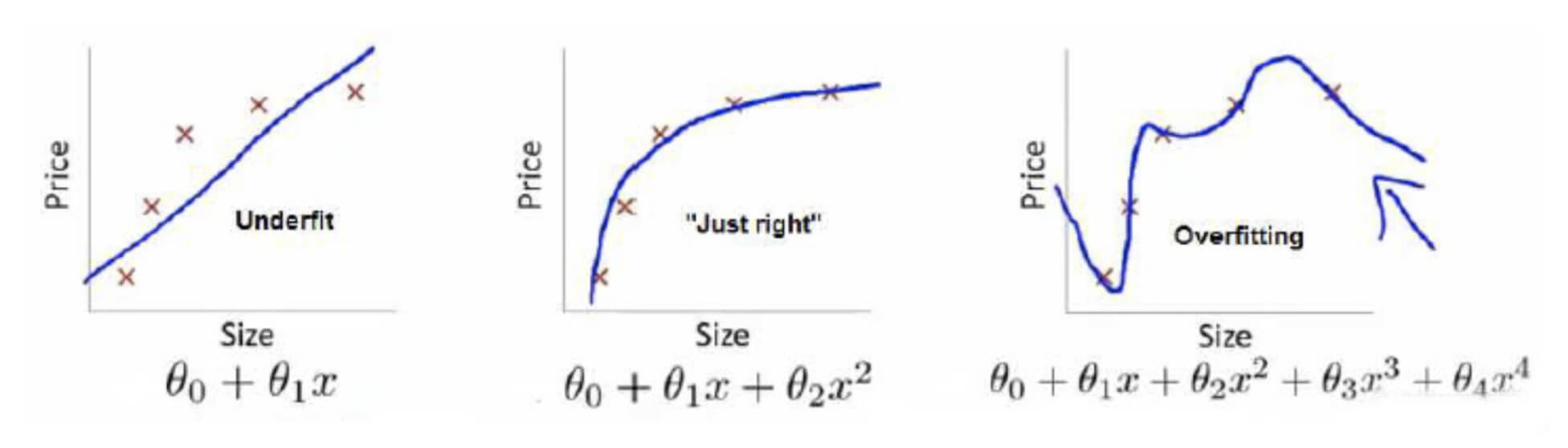
上图的三个函数分别为：$f(x_1);f(x_2);f(x_3)$。

要评价上述三个模型的好坏，引入两个评价指标：

1. 代价函数，即经验风险。
2. 正则化项，专门用于度量模型的复杂度，即结构风险。

最理想的模型：经验风险和结构风险均最小化。

针对上述三个模型：

	经验风险	结构风险
$f(x_1)$	最大	最小
$f(x_2)$	适中	适中
$f(x_3)$	最小	最大

$f(x_3)$可能会过拟合，$f(x_1)$误差过大，$f(x_2)$是比较合适的选择。

3.参考资料

1.机器学习中的目标函数、损失函数、代价函数有什么区别？

---

想要获取最新文章推送或者私聊谈人生，请关注我的个人微信公众号：⬇️x-jeff的AI工坊⬇️

个人博客网站：https://shichaoxin.com

GitHub：https://github.com/x-jeff

---