【机器学习基础】第二课：模型评估方法

【机器学习基础】系列博客为参考周志华老师的《机器学习》一书，自己所做的读书笔记。

1.经验误差与过拟合

• 误差：把学习器的实际预测输出与样本的真实输出之间的差异称为“误差”。
• 训练误差（经验误差）：学习器在训练集上的误差。
• 泛化误差：在新样本上的误差。

过拟合（又称过配）
欠拟合（又称欠配）

过拟合是无法彻底避免的。我们所能做的只是“缓解”，或者说减小其风险。如果可以避免，我们只要追求经验误差最小化即可，这显然是不可能的。

❗️针对“模型选择”问题，理想的解决方案当然是对候选模型的泛化误差进行评估（但是在现实任务中，往往还会考虑时间开销、存储开销、可解释性等方面的因素，这里暂且只考虑泛化误差）。

2.模型评估方法

⚠️通常以测试集的“测试误差”作为泛化误差的近似。

测试集应尽可能与训练集互斥，即测试样本尽量不在训练集中出现，未在训练过程中使用过。

2.1.留出法

“留出法”：直接将数据集D划分为两个互斥的集合，其中一个集合作为训练集S，另一个作为测试集T。

训练/测试集的划分要尽可能保持数据分布的一致性。

一般采用若干次随机划分，重复进行实验评估后取平均值作为留出法的评估结果。

常见做法是将大约$\frac{2}{3}\sim \frac{4}{5}$的样本用于训练，剩余样本用于测试（一般而言，测试集至少应含30个样例）。

2.2.交叉验证法

10折交叉验证示意图：

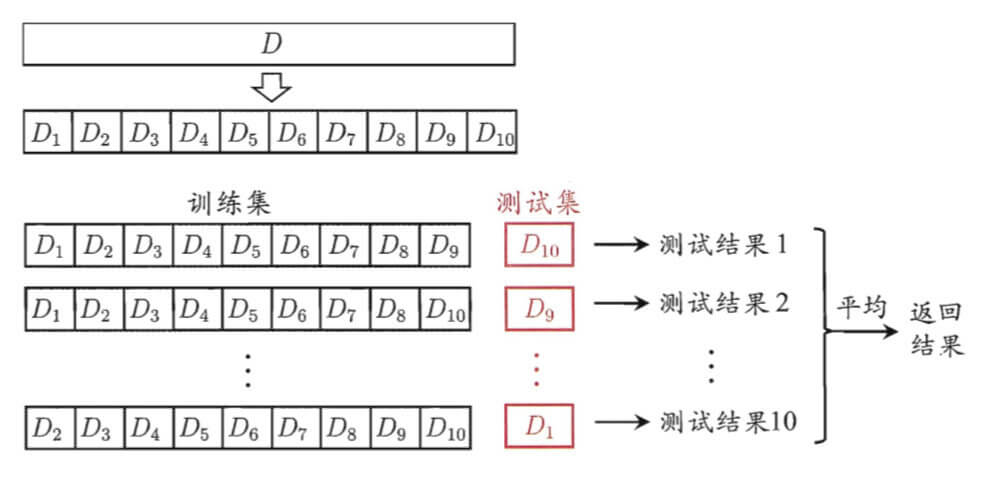
“k折交叉验证”：返回平均结果。进一步，p次k折交叉验证，如10次10折交叉验证。

假定数据集D中包含m个样本，若令$k=m$，则得到了交叉验证法的一个特例：留一法（Leave-One-Out，简称LOO）。

• 优点：留一法使用的训练集与初始数据集相比只少了一个样本，这就使得在绝大多数情况下，留一法中被实际评估的模型与期望评估的用D训练出的模型很相似。因此，留一法的评估结果往往被认为比较准确。
• 缺点：
  1. 在训练集比较大时，训练m个模型的计算开销可能是难以忍受的。
  2. 留一法的评估结果也未必永远比其他评估方法准确。

2.3.自助法

为什么要引入“自助法”？

原因有以下两点：

1. 在留出法和交叉验证法中，由于保留了一部分样本用于测试，因此实际评估的模型所使用的训练集比D小，这必然会引入一些因训练样本规模不同而导致的估计偏差。
2. 留一法受训练样本规模变化的影响较小，但计算复杂度又太高了。

那什么是“自助法”呢？

“自助法”是以自助采样（又称可重复采样、有放回采样）为基础。

给定包含m个样本的数据集D，对它进行采样产生新数据集$D^{\prime }$，每次随机从D中挑选一个样本，将其“拷贝”至$D^{\prime }$，然后将该样本放回D，此过程重复m次，最终得到包含m个样本的数据集$D^{\prime }$。

⚠️自助法有两个要点：1.有放回抽样；2.样本量$D=D^{\prime }$。

很显然，D中一部分样本会在$D^{\prime }$中多次出现，而另一部分样本不出现。

样本在m次采样中始终不被采到的概率是$(1-\frac{1}{m}{)}^m$，取极限得：

$$\underset{m\to \infty }{\lim }(1-\frac{1}{m}{)}^m=[\underset{m\to \infty }{\lim }(1+\frac{1}{-m}{)}^{-m}{]}^{-1}=\frac{1}{e}\approx 0.368$$

关于极限的一些补充知识：

极限和微分的区别：

• 极限是函数当自变量趋向无限大或某一定值时所表现的一种特性。
• 微分是函数在某一点处因变量的增量和自变量增量之间存在的一种特殊关系。

利用四则运算法计算极限：
若$\lim f(x),\lim g(x)$存在❗️（极限过程为$x\to x_0$或$x\to \pm \infty$），则：

1. $\lim [f(x)\pm g(x)]=\lim f(x)\pm \lim g(x)$
2. $\lim c\cdot f(x)=c\lim f(x)$
3. $\lim [f(x)\cdot g(x)]=[\lim f(x)]\cdot [\lim g(x)]$
4. $\lim \frac{f(x)}{g(x)}=\frac{\lim f(x)}{\lim g(x)}$($\lim g(x)\ne 0$)

因此通过自助采样，初始数据集D中约有36.8%的样本未出现在采样数据集$D^{\prime }$中。

可将$D^{\prime }$用作训练集，$D\setminus D^{\prime }$用作测试集（“$\setminus$”表示集合减法），即包外估计（out-of-bag estimate）。

2.4.自助法、留出法、交叉验证法的选择

自助法在数据集小，难以有效划分训练/测试集时很有用；对集成学习等方法有很大好处；但是，自助法产生的数据集改变了初始数据集的分布，会引入估计偏差。

因此，在初始数据量足够时，留出法和交叉验证法更常用一些。

3.调参与最终模型

通常把学得模型在实际使用中遇到的数据称为测试数据，为了加以区分，模型评估与选择中用于评估测试的数据集常称为“验证集”。

---

想要获取最新文章推送或者私聊谈人生，请关注我的个人微信公众号：⬇️x-jeff的AI工坊⬇️

个人博客网站：https://shichaoxin.com

GitHub：https://github.com/x-jeff

---