图形学 直线算法

1.DDA算法

我们在画直线时我们取的像素都在确定的两个像素里选择。

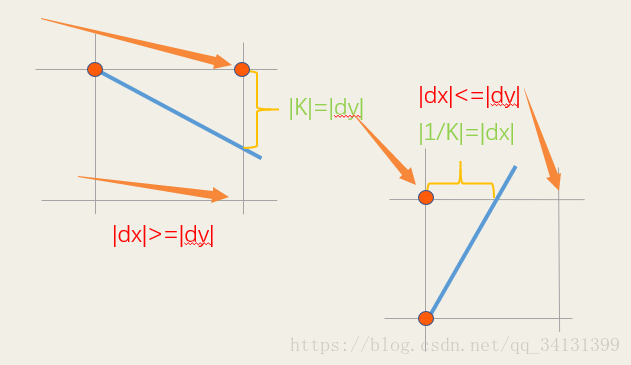
DDA直线算法在于利用K或者K的倒数，我们都知道k=dy/dx,所以是单位x内y的变化。

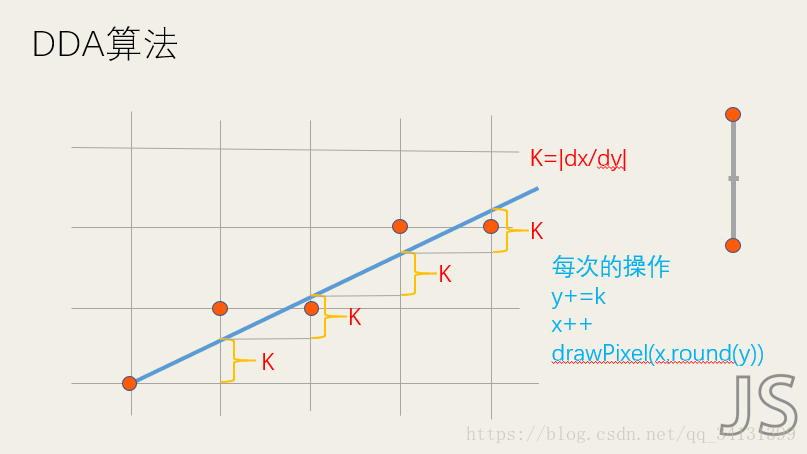
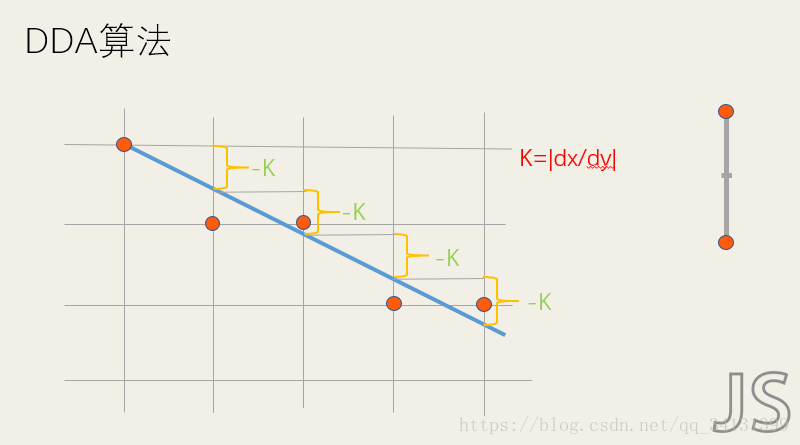
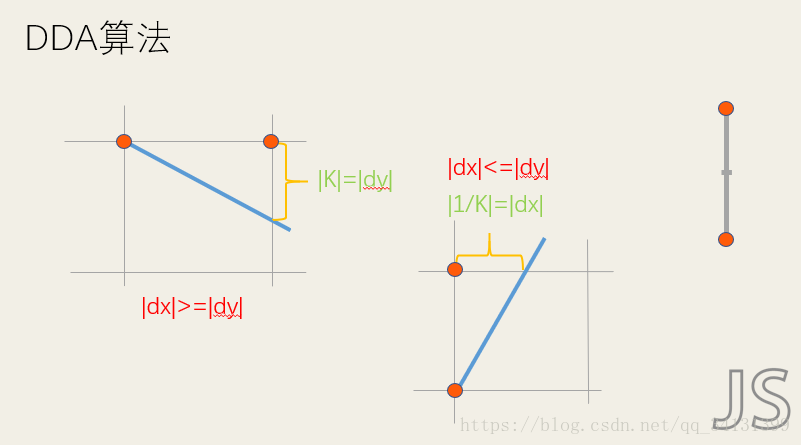
    不过在屏幕内我们通常以像素为单位，所以当|k|<1时我们以dx=1，dy=k。当|k|>=1,我们发现y比x走的多，|dy/dx|>1即dy>dx,所以为了在机器中我们以y走一个像素，x增加1/k。

    优点：比较易于实现，贴近数学

    缺点：有浮点数的处理（k的取整，浮点数的加法），效率不高

代码如下：

// DDA直线算法
function DDALine(x0,y0,x1,y1,color) {

  // 定义初始化参数
  var dx,dy,k,y;
  y=y0;
  x=x0;
  dx=0.0+x1-x0;
  dy=0.0+y1-y0;
  k=dy/dx;
  kReciprocal=dx/dy;

  // 根据点的位置关系（判断大小）、以及斜率将初始点设置好
  if (Math.abs(k)<1) {
    var xMax=x0>x1?x0:x1;
    var xMin=x0<x1?x0:x1;
    var yMax=xMin!=x0?y0:y1;
    var yMin=xMin==x0?y0:y1;

    // 根据增量k来画点
    for (var xn=xMin; xn<=xMax;) {
      drawPixel(xn,Math.floor(yMin+0.5),aposLocation,context);
      xn++;
      yMin+=k;
    }
  }else {
    var yMax=y0>y1?y0:y1;
    var yMin=y0<y1?y0:y1;
    var xMax=yMin!=y0?x0:x1;
    var xMin=yMin==y0?x0:x1;
    for (var yn=yMin; yn<=yMax;) {
      drawPixel(Math.floor(xMin+0.5),yn,aposLocation,context);
      yn++;
      xMin+=kReciprocal;
    }
  }
}

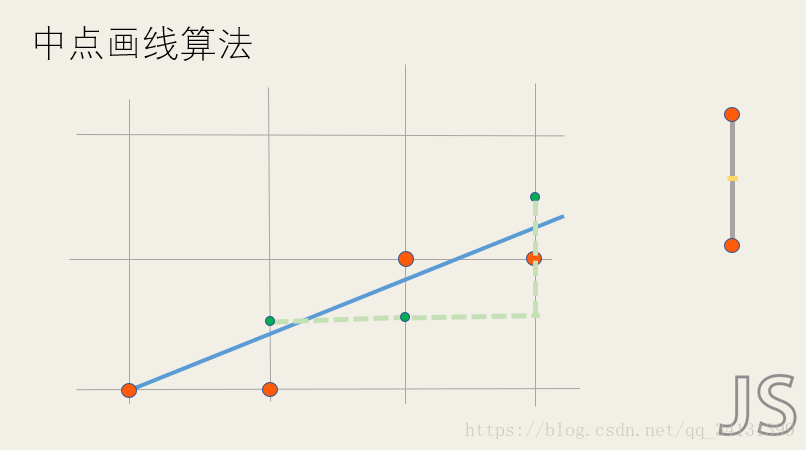
2.中点画线算法

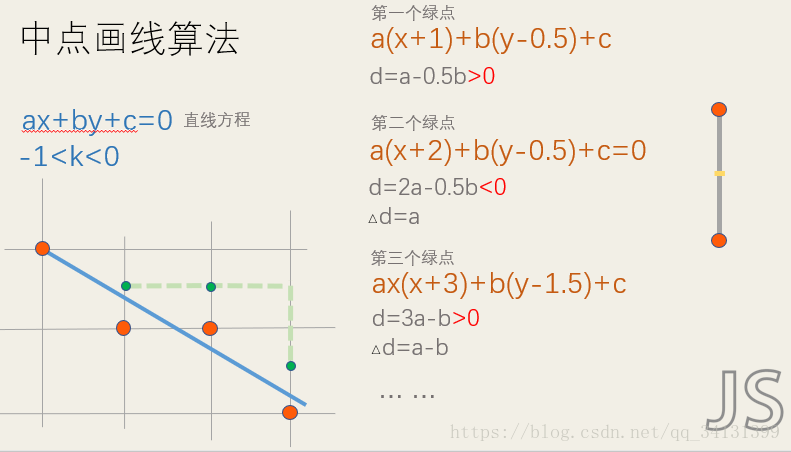
中点画线就是以中点到直线的距离判断取点的位置，若中点带入直线,判断符号就能决策取哪个点。但是我们的k取不同值时，我们的判别式以及判别式增量需要变化。

    优点：进一步减少了浮点数的运算

代码如下:

// 中点直线画线
function MidPointLine(x0,y0,x1,y1,color) {


  var dx,dy,k,y,x;
  var a,b,d1,d2,d;
  dx=0.0+x1-x0;
  dy=0.0+y1-y0;
  k=dy/dx;
  kReciprocal=dx/dy;
  y=y0;x=x0;


  // 根据k的值来设置起始点
  if (Math.abs(k)<1) {
    var xMax=x0>x1?x0:x1;
    var xMin=x0<x1?x0:x1;
    var yMax=xMin!=x0?y0:y1;
    var yMin=xMin==x0?y0:y1;
  }else {
    var yMax=y0>y1?y0:y1;
    var yMin=y0<y1?y0:y1;
    var xMax=yMin!=y0?x0:x1;
    var xMin=yMin==y0?x0:x1;
  }


  x0=xMin;x1=xMax;y0=yMin;y1=yMax;y=y0;x=x0;


  if (Math.abs(k)<1) {
    a=y0-y1;
    b=x1-x0;
    b=k>0?b:-b;
    d=2*a+b;
    d1=k>0?2*a:2*(a+b);
    d2=k>0?2*(a+b):2*a;


    // 根据k的正负确定每次增加或减少
    var uFactor=k>0?1:0;
    var dFactor=k>0?0:-1;
    drawPixel(x,y,aposLocation,context);
    while (x<x1) {
      if (d<0) {
        x++;y+=uFactor;d+=d2;
      }else {
        x++;y+=dFactor;d+=d1;
      }
      drawPixel(x,y,aposLocation,context);
    }
  }else {
    a=x0-x1;
    b=y1-y0;
    b=k>0?b:-b;
    d=2*a+b;
    d1=k>0?2*a:2*(a+b);
    d2=k>0?2*(a+b):2*a;
    var dFactor=k>0?0:-1;
    var uFactor=k>0?1:0;
    drawPixel(x,y,aposLocation,context);
    while (y<y1) {
      if (d<0) {
        x+=uFactor;y++;d+=d2;
      }else {
        y++;x+=dFactor;d+=d1;
      }
      drawPixel(x,y,aposLocation,context);
    }
  }
}

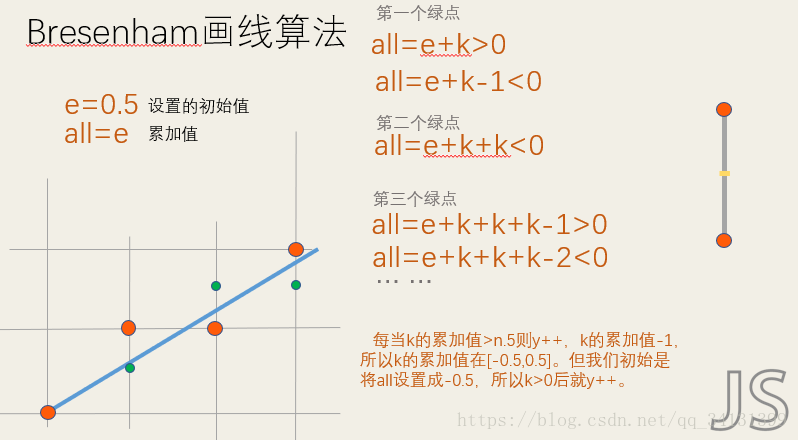
3.Bresenham画线算法

这里是提前引入一个初值，然后后边不断累加一个增量来判断符号来判断点的位置。虽然引入0.5但是我们乘二就可以解决浮点数的问题，这个其实是DDA的变种，原理相似但是更为高级的是引入初始的判别值，经过变形去掉了浮点数，也只有一个增量。更易于机器的实现。

function BresenhamLine(x0,y0,x1,y1,color) {
  var x,y,dx,dy,c,dy_2,dx_2,e,k,kReciprocal;

  k=(y1-y0)/(x1-x0);

  if (Math.abs(k)<1) {
    var xMax=x0>x1?x0:x1;
    var xMin=x0<x1?x0:x1;
    var yMax=xMin!=x0?y0:y1;
    var yMin=xMin==x0?y0:y1;
  }else {
    var yMax=y0>y1?y0:y1;
    var yMin=y0<y1?y0:y1;
    var xMax=yMin!=y0?x0:x1;
    var xMin=yMin==y0?x0:x1;
  }

  x0=xMin;x1=xMax;y0=yMin;y1=yMax;y=y0;x=x0;

  dx=x1-x0;dy=y1-y0;e=-dx;
  x=x0;y=y0;
  dy_2=2*dy;
  dx_2=2*dx;


  if (Math.abs(k)<1) {
    if (k>0) {
      for (var i = 0; i <=dx; i++) {
        drawPixel(x,y,aposLocation,context);
        x++;e=e+dy_2;
        if (e>=0) {
          y++;e=e-dx_2;
        }
      }
    }else{
      e=-e;
      for (var i = 0; i <=dx; i++) {
        drawPixel(x,y,aposLocation,context);
        x++;e=e+dy_2;
        if (e<=0) {
          y--;e=e+dx_2;
        }
      }
    }
  }else{
      if (k>0) {
        for (var i = 0; i <=dy; i++) {
          drawPixel(x,y,aposLocation,context);
          y++;e=e+dx_2;
          if (e>=0) {
            x++;e=e-dy_2;
          }
        }
      }else {
        e=-e;
        for (var i = 0; i <=dy; i++) {
          drawPixel(x,y,aposLocation,context);
          y++;e=e+dx_2;
          if (e<=0) {
            x--;e=e+dy_2;
          }
        }
    }

  }

}