IEEE754浮点数及其运算

一个二进制浮点数可以表示为：

• 数的符号
• 一些有效位
• 有符号的比例因子系数（隐含的基数为2）

结构如图所示（单精度）

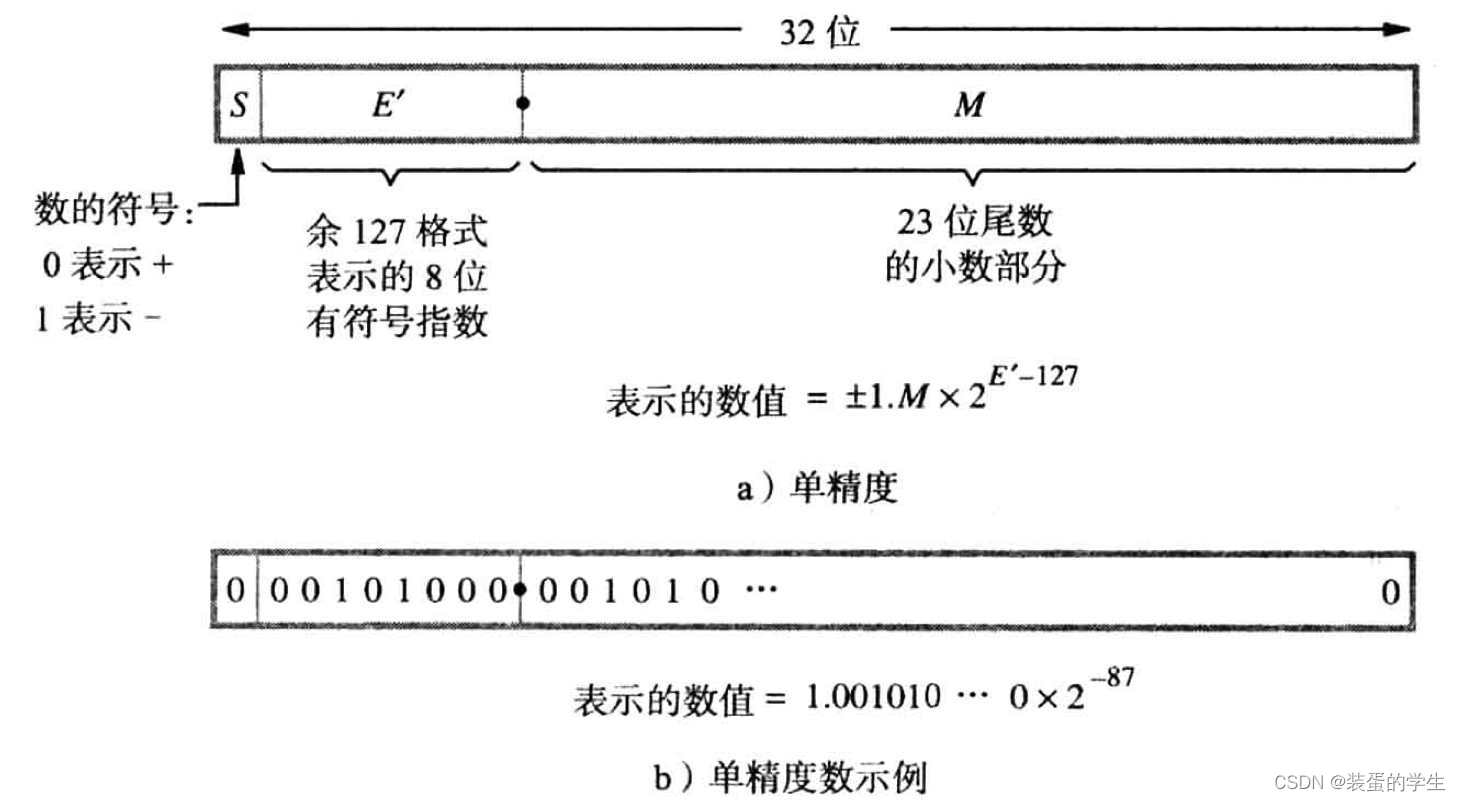
如果是双精度浮点数，则是1位符号位+11位余1023格式的指数+52位尾数

规格化：当二进制小数点位于第一个有效位的右方时，我们说这个数是规格化(Normalized)的。

特殊值

余127指数E’的端点值0和255被用来表示特殊值。

当E’=255且M=0时，表示∞。这里的∞时用0去除一个正常数的结果。这些表示中仍然使用符号位，因此存在±0和±∞的表示。

当E’=0且M≠0时，表示的是非规格化数， 其值为±0.Mx2^-126。因此它比最小的规格化数还小。

当E’=255且M≠0时，表示的数称为非数。即NaN，表示执行非法操作的结果。

浮点数算术运算

1.加/减法规则

1. 选取指数较小的数，将其尾数右移，右移的步数等于两指数之差。
2. 将结果的指数设为与较大的指数相等。
3. 对尾数进行加/减运算，并确定结果的符号。
4. 如果必要，对结果的值进行规格化。

乘除法比加减法要简单些，因为不需要对齐尾数。

2.乘法规则

1. 将指数相加并减去127以保持余127表示。
2. 将尾数相乘并确定结果的符号。
3. 如果必要，对结果的值进行规格化。

3.除法规则

1. 将指数相减并加上127以保持余127表示。
2. 将尾数相除并确定结果的符号。
3. 如果必要，对结果的值进行规格化。

转载请注明来源：IEEE754浮点数及其运算 | 龙进的博客