引言
线性回归是最简单的机器学习算法,说白了就是构造一元或者多元的线性方程,然后根据现有样本数据进行函数拟合,求解出线性方程的各个参数,之后就可以通过该线性方程进行相关预测。
模拟场景
根据常识,一个人的工龄越长,那么这个人的工资也会随之增加。那么,我们现在想要知道,工龄对工资之间具体存在什么样的数学关系。
巧妇难为无米之炊,先放上一组数据:
| 工龄(年) | 工资(元) |
|---|---|
| 1.1 | 39343.00 |
| 1.3 | 46205.00 |
| 1.5 | 37731.00 |
| 2.0 | 43525.00 |
| 2.2 | 39891.00 |
| 2.9 | 56642.00 |
| 3.0 | 60150.00 |
| 3.2 | 54445.00 |
| 3.2 | 64445.00 |
| 3.7 | 57189.00 |
| 3.9 | 63218.00 |
| 4.0 | 55794.00 |
| 4.0 | 56957.00 |
| 4.1 | 57081.00 |
| 4.5 | 61111.00 |
| 4.9 | 67938.00 |
| 5.1 | 66029.00 |
| 5.3 | 83088.00 |
| 5.9 | 81363.00 |
| 6.0 | 93940.00 |
| 6.8 | 91738.00 |
| 7.1 | 98273.00 |
| 7.9 | 101302.00 |
| 8.2 | 113812.00 |
| 8.7 | 109431.00 |
| 9.0 | 105582.00 |
| 9.5 | 116969.00 |
| 9.6 | 112635.00 |
| 10.3 | 122391.00 |
| 10.5 | 121872.00 |
构造方程
根据这些样本数据,可以得出下面的散点图:
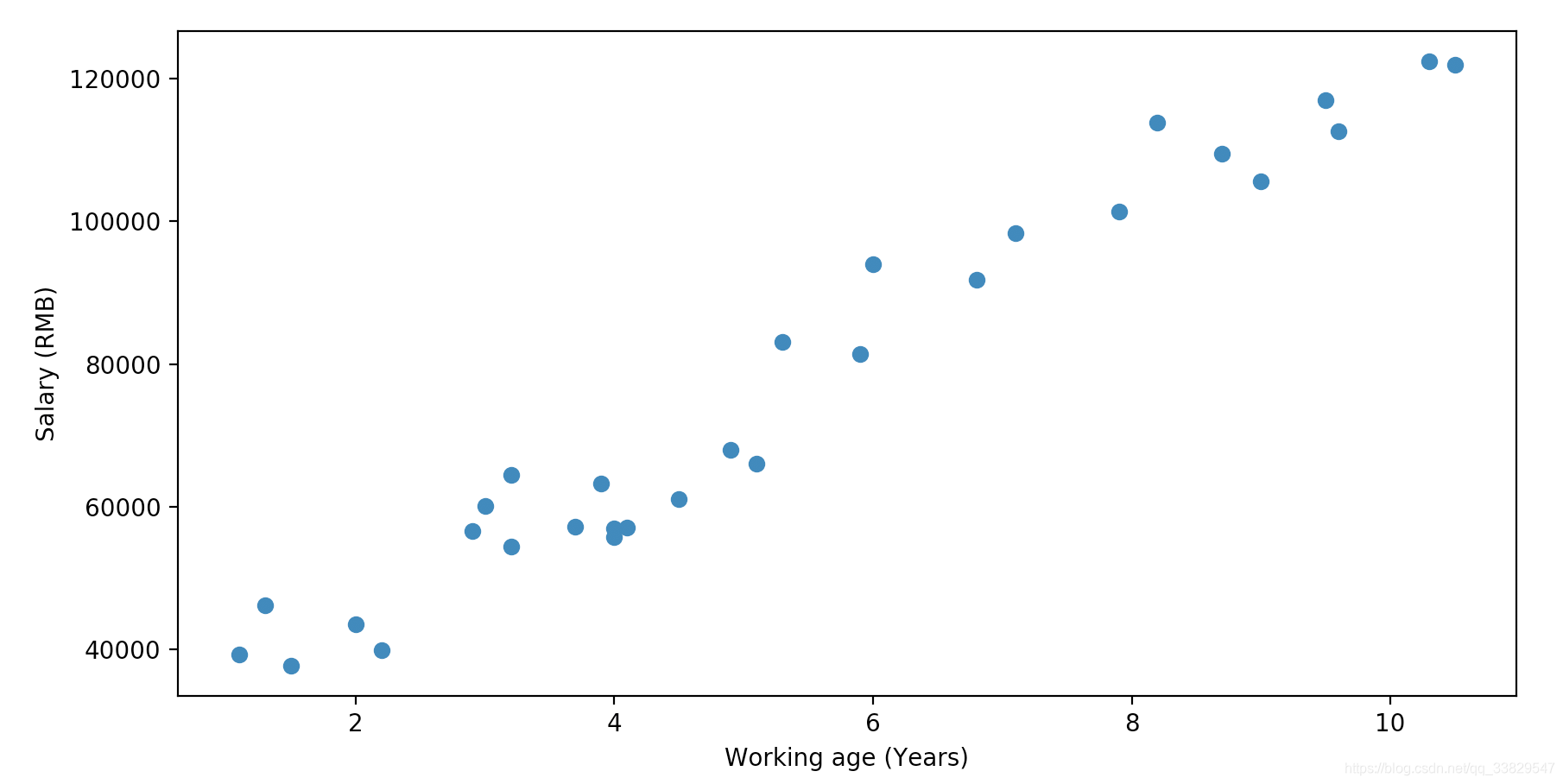
这里我们可以根据散点图的大致走向进行猜测,工龄x与工资y之间是一元线性关系,于是我们可以写出如下线性方程:
h(x)=θ0+xθ1 h(x)= \theta_0 + x \theta_1 h(x)=θ0+xθ1
其中:
- h(x)h(x)h(x)是最终的工资
- xxx是自变量工龄
- θ1\theta_1θ1是与工龄相关的参数
- θ0\theta_0θ0是偏置项
上述是线性方程最简单的形式,更普遍的情况下可能会有nnn个特征值,即以下这种形式:
h(x)=θ0+x1θ1+x2θ2+...+xnθn=x0⏞x0=1θ0+x1θ1+x2θ2+...+xnθn=∑i=0n(xiθi) \begin{aligned} h(x) & = \theta_0 + x_1 \theta_1 + x_2 \theta_2+...+x_n \theta_n \\ & = \overbrace{x_0}^{x_0=1} \theta_0 + x_1\theta_1 + x_2\theta_2+...+x_n\theta_n \\ & = \sum_{i=0}^n(x_i\theta_i) \end{aligned} h(x)=θ0+x1θ1+x2θ2+...+xnθn=x0x0=1θ0+x1θ1+x2θ2+...+xnθn=i=0∑n(xiθi)
由于机器学习中基本使用矩阵进行运算,为了后续数学推导,因此我们将上述式子改写为矩阵的形式:
h(x)=∑i=0n(θixi)=[x0x1...xn]×[θ0θ1...θn]=XΘ \begin{aligned} h(x) & = \sum_{i=0}^n(\theta_ix_i) \\ & = \left[ \begin{array}{c} x_0 \\ x_1 \\ ... \\ x_n \\ \end{array} \right] \times \left[ \begin{array}{c} \theta_0 & \theta_1 & ... & \theta_n\\ \end{array} \right]\\ & = X \Theta \\ \end{aligned} h(x)=i=0∑n(θixi)=⎣⎢⎢⎡x0x1...xn⎦⎥⎥⎤×[θ0θ1...θn]=XΘ
其中:
- Θ\ThetaΘ为方程参数的列矩阵形式
- XXX为方程自变量的行矩阵形式
误差项
接下来,我们要考虑到实际值与线性方程的解肯定会存在误差,这里我们用ϵ\epsilonϵ来表示误差项:
y真实值=(XΘ)预测值+ϵ误差项(1) y^{真实值} =(X \Theta)^{预测值} + \epsilon^{误差项} \tag 1 y真实值=(XΘ)预测值+ϵ误差项(1)
我们当然希望误差项ϵ\epsilonϵ越小越好,这里我们假定误差项ϵ\epsilonϵ是独立的并且服从均值为000、方差为θ2\theta^2θ2的高斯分布:
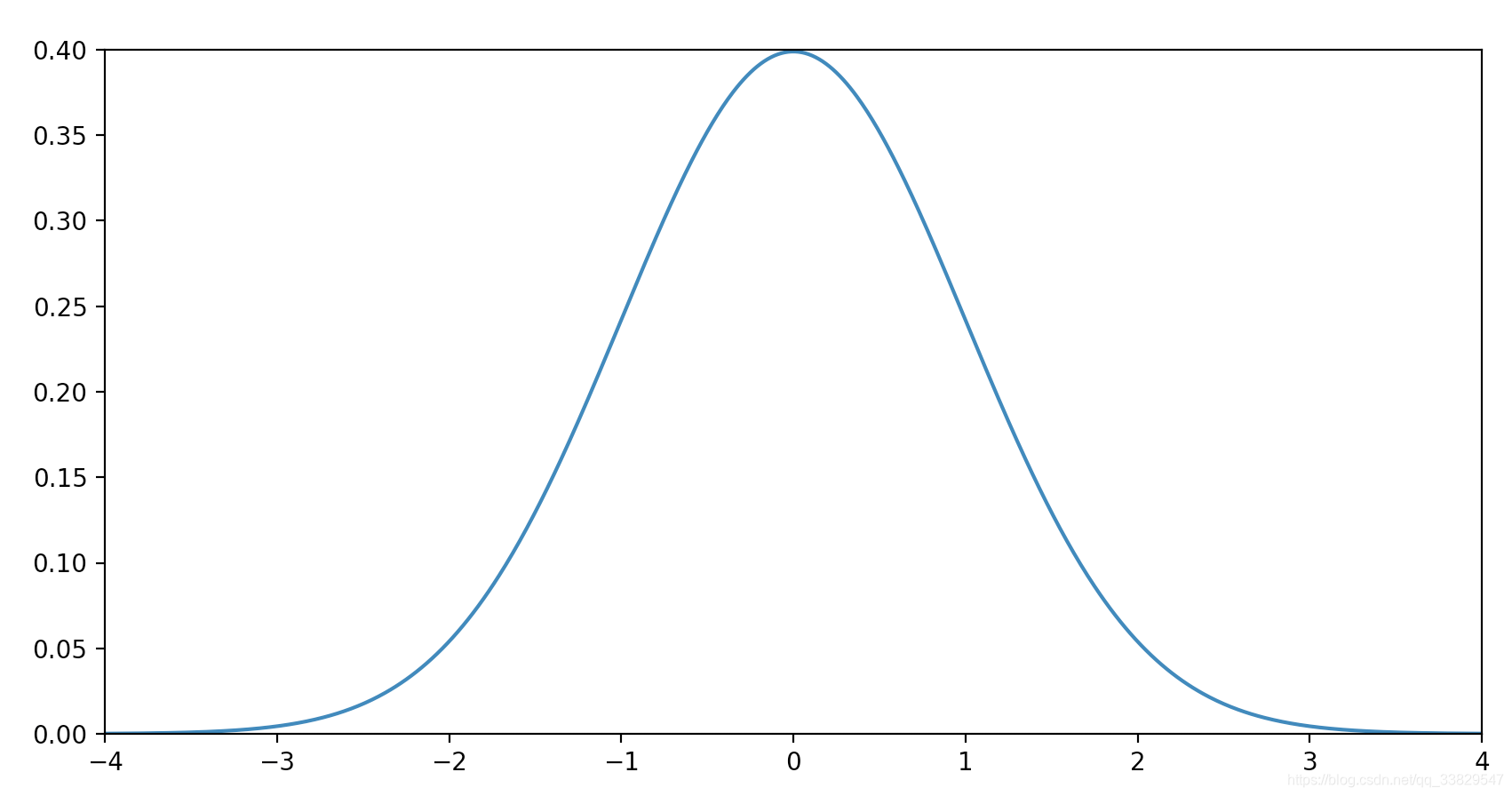
- 独立表示各个样本之间的误差之间毫无干系
- 均值为0的意义是概率集中在误差为0的情况
我们可以直接写出每一个样本的误差项ϵ\epsilonϵ的概率函数
p(ϵ(i))=12πσexp(−(ϵ(i))22σ2)(2) p(\epsilon^{(i)}) = \frac{1}{\sqrt[]{2\pi}\sigma} \exp(- \frac{(\epsilon^{(i)})^2}{2\sigma^2}) \tag 2 p(ϵ(i))=2πσ1exp(−2σ2(ϵ(i))2)(2)
结合(1)(2)(1)(2)(1)(2)可得:
p(ϵ(i))=12πσexp(−(y(i)−X(i)Θ)22σ2)(3) p(\epsilon^{(i)}) = \frac{1}{\sqrt[]{2\pi}\sigma} \exp(- \frac{(y^{(i)}-X^{(i)}\Theta )^2}{2\sigma^2}) \tag 3 p(ϵ(i))=2πσ1exp(−2σ2(y(i)−X(i)Θ)2)(3)
我们最终的目的是求出线性方程,换句话说,也就是将方程中的参数Θ\ThetaΘ算出来。那该怎么求呢?这里我们就要用到似然函数。
似然函数与最大似然估计
没学过同学很可能会懵逼,似然函数又是个什么玩意?百科上的定义如下:
似然函数是一种关于统计模型参数的函数。给定输出x时,关于参数θ的似然函数L(θ|x)(在数值上)等于给定参数θ后变量X的概率:L(θ|x)=P(X=x|θ)。
感觉这个定义还是太学术化了?没关系,我举一个栗子?
我们知道硬币有正反两面,并且我们一般认为,如果将硬币抛出去,正面朝上和反面朝上的概率都是0.5。
好,现在条件变了,假设我们并不知道一枚硬币被抛出去后正面和反面朝上的概率分别是多少,但我们现在想知道两者的概率,该怎么做呢?
我们进行10次抛硬币的实验并得到了一组实验结果样本,6次正面朝上,4次反面朝上。我们可以设这枚硬币正面朝上的概率为ppp,反面朝上的概率为1−p1-p1−p。这组10次抛硬币样本发生的概率等于各个样本发生概率的乘积:
L=p6(1−p)4 L = p^6(1-p)^4 L=p6(1−p)4
这个LLL就叫似然函数。
可惜的是,根据上面的似然函数,我们是没有办法直接求出ppp的值,因为LLL是不确定的,而ppp的取值可能是(0,1)(0,1)(0,1)之间的任何值。更通俗的说法是,即使正面和反面朝上的概率相等,也可能会发生投出10次硬币结果10次都正面朝上的事件。
既然如此,那我们该怎么求出ppp值呢?这里就要用到最大似然估计法。
通俗地说,最大似然估计就是不要去考虑什么ppp只有0.00001但是10次实验发生6次正面朝上的小概率情况,而是考虑什么样的取值可以让似然函数的值最大。在这个抛硬币的案例中等同于什么样的ppp可以让LLL最大。
那么这个问题就转换为了函数求极大值的问题了,具体方法是对似然函数LLL求导,然后算出导数为0时的ppp,也就是极值点。
慢着,是不是觉得LLL很难求导?没错,对LLL直接进行求导太复杂了,因此我们取对数函数,然后根据公式ln(AB)=ln(A)+ln(B)\ln(AB) = \ln(A) + \ln(B)ln(AB)=ln(A)+ln(B),将原式由乘法转化为加法:
ln(L)=ln(p6(1−p)4)=ln(p6)+ln(1−p)4=6ln(p)+4ln(1−p) \begin{aligned} \ln(L) & = \ln(p^6(1-p)^4) \\ & = \ln(p^6) + \ln(1-p)^4 \\ & = 6\ln(p) + 4\ln(1-p) \end{aligned} ln(L)=ln(p6(1−p)4)=ln(p6)+ln(1−p)4=6ln(p)+4ln(1−p)
现在我们再对ln(L)\ln(L)ln(L)求导,算出来的p(正)p_{(正)}p(正)是一样的,因为对数函数不改变原函数的单调性:
L′=6p−41−p L' = \frac{6}{p} - \frac{4}{1-p} L′=p6−1−p4
在求出导数为000时的ppp值:
6p−41−p=0p=0.6 \begin{aligned} &\frac{6}{p} - \frac{4}{1-p} = 0 \\ &p = 0.6 \end{aligned} p6−1−p4=0p=0.6
因此硬币正面朝上的概率为0.6,反面朝上的概率为0.4。这样我们就完成了根据一组10次抛硬币的样本,反推出硬币正反面朝上的概率分别是多少。
这就是似然函数和最大似然估计的用法,现在回到我们的案例。
回到我们的案例
我们刚才说了,误差项ϵ\epsilonϵ的概率函数服从高斯分布,那么我们这一组样本关于误差项的似然函数等于每一个样本的误差项的概率密度的乘积。结合之前的式子(3)(3)(3)可得:
L=∏i=1mp(ϵ(i))=∏i=1m12πσexp(−(y(i)−X(i)Θ)22σ2)(4) \begin{aligned} L & = \prod_{i=1}^{m}p(\epsilon^{(i)})\\ & = \prod_{i=1}^{m}\frac{1}{\sqrt[]{2\pi}\sigma} \exp(- \frac{(y^{(i)}-X^{(i)}\Theta )^2}{2\sigma^2}) \tag 4 \end{aligned} L=i=1∏mp(ϵ(i))=i=1∏m2πσ1exp(−2σ2(y(i)−X(i)Θ)2)(4)
其中mmm为样本的个数,iii指代具体的某一个样本的序号。
接下来取对数函数:
ln(L)=ln∏i=1m12πσexp(−(y(i)−X(i)Θ)22σ2)=mln12πσ−1σ2×12∑i=1m(y(i)−X(i)Θ)2(5) \begin{aligned} \ln(L) & = \ln \prod_{i=1}^{m}\frac{1}{\sqrt[]{2\pi}\sigma} \exp(- \frac{(y^{(i)}-X^{(i)}\Theta)^2}{2\sigma^2}) \\ & = m\ln \frac{1}{\sqrt[]{2\pi}\sigma} - \frac{1}{\sigma^2} \times \frac{1}{2} \sum_{i=1}^{m}(y^{(i)}-X^{(i)}\Theta)^2 \tag 5 \end{aligned} ln(L)=lni=1∏m2πσ1exp(−2σ2(y(i)−X(i)Θ)2)=mln2πσ1−σ21×21i=1∑m(y(i)−X(i)Θ)2(5)
现在我们需要求出,什么样的Θ\ThetaΘ可以使得对数似然函数ln(L)\ln(L)ln(L)得到最大值。
可以看出,上式(5)(5)(5)只有减号右边的部分与Θ\ThetaΘ有关,而由于减号的关系,我们只要让右边部分越小越好。
因此,我们的目标就是,对下面这个式子求关于Θ\ThetaΘ的偏导,算出导数为0时Θ\ThetaΘ的取值:
J(Θ)=12∑i=1m(y(i)−X(i)Θ)2(6) J(\Theta) = \frac{1}{2}\sum_{i=1}^{m}(y^{(i)}-X^{(i)}\Theta )^2 \tag 6 J(Θ)=21i=1∑m(y(i)−X(i)Θ)2(6)
这个J(Θ)J(\Theta)J(Θ)被称为目标函数,因为这个函数是我们这个案例最终被抽象为的、我们所追求的目标形式。
但是直接求导似乎也有些困难,那么我们把上式(6)(6)(6)整体转化为矩阵的形式:
J(Θ)=12(y−XΘ)T(y−XΘ)=12(yT−ΘTXT)(y−XΘ)=12(yTy−ΘTXTy−yTXΘ+ΘTXTXΘ)(7) \begin{aligned} J(\Theta) & = \frac{1}{2}(y-X\Theta)^T(y-X\Theta ) \\ & = \frac{1}{2}(y^T-\Theta^TX^T)(y-X\Theta) \\ & = \frac{1}{2}(y^Ty-\Theta^TX^Ty-y^TX\Theta +\Theta^TX^TX\Theta) \tag 7 \end{aligned} J(Θ)=21(y−XΘ)T(y−XΘ)=21(yT−ΘTXT)(y−XΘ)=21(yTy−ΘTXTy−yTXΘ+ΘTXTXΘ)(7)
以上用到了矩阵转置的运算规律:
(A+B)T=AT+BT (AB)T=BTAT(A+B)^T=A^T+B^T \space \space (AB)^T=B^TA^T(A+B)T=AT+BT (AB)T=BTAT
求J(Θ)J(\Theta)J(Θ)关于Θ\ThetaΘ的偏导数:
∂J(Θ)∂Θ=12(−XTy−(yTX)T+2XTXΘ)=12(−2XTy+2XTXΘ)=XTXΘ−XTy(8) \begin{aligned} \frac{\partial J(\Theta)}{\partial \Theta} & = \frac{1}{2}(-X^Ty-(y^TX)^T+2X^TX\Theta) \\ & = \frac{1}{2}(-2X^Ty+2X^TX\Theta) \\ & = X^TX\Theta - X^Ty \tag 8 \end{aligned} ∂Θ∂J(Θ)=21(−XTy−(yTX)T+2XTXΘ)=21(−2XTy+2XTXΘ)=XTXΘ−XTy(8)
以上过程用到了矩阵求偏导的公式:
dXTAXdX=2AX dXTAdX=A dXAdX=AT\frac{dX^TAX}{dX}=2AX \space \space \frac{dX^TA}{dX}=A \space \space\frac{dXA}{dX}=A^TdXdXTAX=2AX dXdXTA=A dXdXA=AT
求偏导数等于000时的Θ\ThetaΘ:
XTXΘ−XTy=0XTXΘ=XTyΘ=(XTX)−1XTy(9) \begin{aligned} &X^TX\Theta - X^Ty = 0 \\ &X^TX\Theta = X^Ty \\ &\Theta=(X^TX)^{-1}X^Ty \tag 9 \end{aligned} XTXΘ−XTy=0XTXΘ=XTyΘ=(XTX)−1XTy(9)
上式解出了Θ\ThetaΘ的值,XXX为样本的特征值,yyy为样本的实际值,都是已知的,带入计算即可:
Θ=([1.11.2...10.5]×[1.11.2...10.5])−1×[1.11.2...10.5]×[3934346205...121872] \begin{aligned} \Theta & = ( \left[ \begin{array}{c} 1.1&1.2& ...& 10.5 \end{array} \right] \times \left[ \begin{array}{c} 1.1 \\ 1.2 \\ ... \\ 10.5 \end{array} \right] )^{-1} \times \left[ \begin{array}{c} 1.1&1.2& ...& 10.5 \end{array} \right]\times \left[ \begin{array}{c} 39343 \\ 46205 \\ ... \\ 121872 \end{array} \right] \end{aligned} Θ=([1.11.2...10.5]×⎣⎢⎢⎡1.11.2...10.5⎦⎥⎥⎤)−1×[1.11.2...10.5]×⎣⎢⎢⎡3934346205...121872⎦⎥⎥⎤
计算量十分大,一般这里都使用程序进行计算,最后求解出Θ\ThetaΘ的值为:
Θ=[25792.20019867,9449.96232146] \Theta = [25792.20019867,9449.96232146] Θ=[25792.20019867,9449.96232146]
即:
θ0=25792.20019867θ1=9449.96232146 \begin{aligned} &\theta_0 = 25792.20019867 \\ &\theta_1 = 9449.96232146 \end{aligned} θ0=25792.20019867θ1=9449.96232146
因此可得拟合出的线性回归方程:
h(x)=9449.96232146x+25792.20019867 h(x) = 9449.96232146x + 25792.20019867 h(x)=9449.96232146x+25792.20019867
手写线性回归算法
弄清楚线性回归算法背后的数学原理后,编写线性回归算法的代码就容易了。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def linear_model(thetas, X):
'''线性模型的矩阵形式
'''
result = []
for x in X:
result.append(np.dot(thetas.reshape(len(thetas)), x))
return result
def solve(X, y):
'''求解θ
'''
return np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
if __name__ == "__main__":
pdData = pd.read_csv("Salary_Data.csv", sep=",", header=None)
pdData.insert(0, "x0", 1)
orig_data = pdData.values
cols = orig_data.shape[1]
# 拿到特征值(包含x0)
X = orig_data[:, 0:cols-1]
# 拿到特征值(不包含x0)
x = orig_data[:, 1:cols-1]
# 拿到实际值
y = orig_data[:, cols-1:cols]
# 求解θ
thetas = solve(X, y)
print(thetas)
# 求解预测值
y_predict = linear_model(thetas, X)
plt.figure(figsize=(10, 5))
# 画出实际值的散点图
plt.scatter(pdData.iloc[:, 1], pdData.iloc[:, 2])
plt.xlabel("Working age (Years)")
plt.ylabel("Salary (RMB)")
# 画出线性回归方程的图像
plt.plot(x, y_predict)
plt.show()
最终结果:
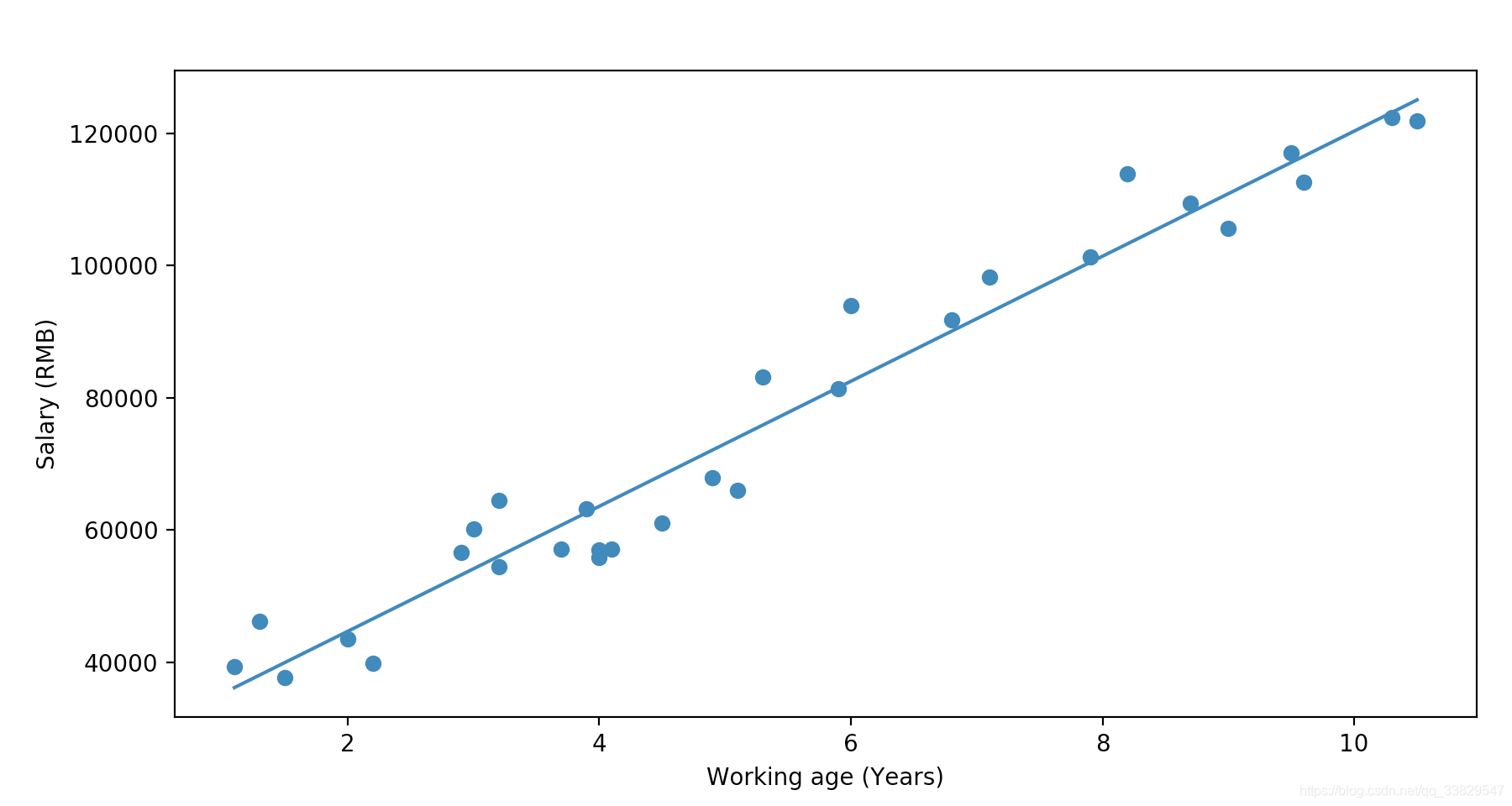


























 918
918

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










