学习《统计学习方法》第一章-概论

我是chios

于 2019-05-14 17:11:57 发布

阅读量311

点赞数

分类专栏：统计学习方法机器学习文章标签：统计学习方法机器学习

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/qq_33331451/article/details/90145572

版权

机器学习同时被 2 个专栏收录

8 篇文章

订阅专栏

统计学习方法

4 篇文章

订阅专栏

前言：最近学习吴恩达老师的《机器学习》，其中对统计学习知识运用有一定的要求。所以根据网上推荐，学习李航博士的《统计学习方法》。一来写博客有助于将来回忆，二来可以与网友分享，三来也是给自己勉励。

目录

第1章：统计学习方法概论

1.1统计学习

1.2监督学习

1.3 统计学习三要素

1.4 模型评估与模型选择

1.5 正则化与交叉验证

1.5.1 正则化

1.5.2 交叉验证

1.6 泛化能力

1.7 生成模型与判别模型

1.8 分类问题

1.9 标注问题

1.10 回归问题

第1章：统计学习方法概论

第1章介绍统计学习的定义、研究对象和方法。

介绍有：

统计学习三要素：模型、策略和算法；模型选择（正则化、交叉验证和学习的泛化能力）；

生成模型与判别模型；

监督学习方法：分类问题、标注问题和回归问题。

1.1统计学习

统计学习包括：监督学习、非监督学习、半监督学习以及强化学习。

统计学习特点

统计学习以数据为驱动，目的是对数据进行预测和分析，以方法为中心。

2.统计学习对象

统计学习对象是数据，提取数据特征，抽出数据模型，发现模型知识，回到数据的分析与预测中。

3.统计学习目的

目的是对数据进行预测和分析，是通过构建概率统计模型实现。

4.统计学习方法

得到一个有限的训练数据集合；
确定包含所有可能的模型的假设空间，即学习模型的集合；
确定模型选择的准则，即学习模型的集合；
实现求解最优模型算法，即学习的算法；
通过学习方法选择最优模型；
利用学习的最优模型对新数据进行预测或分析。

1.2监督学习

inputX(特征向量) ->特征空间->输出空间Y

input: $x_{}i = (x^{(1)}_{}i,x^{(2)}_{}i,...,x^{(i)}_{}i,...,x^{(n)}_{}i)^{T}$

输入和输出变量不同类型，对于连续变量预测问题称为回归问题；

输入变量和输出变量为有限离散变量预测称为分类问题

输入变量和输出变量为变量序列的预测问题称为标注问题。

联合概率分布

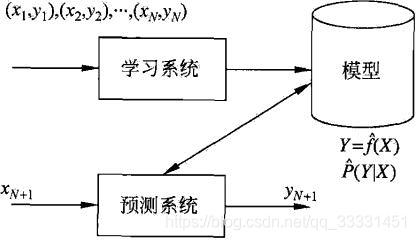
监督学习输入与输出随机变量X和Y遵循联合概率分布P(X,Y)。

假设空间

假设空间就是监督学习的一个输入到输出的映射，这一映射由模型表示，学习就是为了找到最好的模型。模型属于由输入空间到输出空间的映射集合，这个集合就是假设空间。

1.3 统计学习三要素

方法=模型+策略+算法

1.3.1 模型

监督学习，模型就是所要学习的条件概率分布或决策函数。

1.3.2 策略

策略就是按照什么样的规则选择或学习最优的模型。在监督学习中，就是在假设空间 $F$ 中选择最优模型 $f$ 作为决策函数。

1.损失函数和风险函数

损失函数：用来度量预测错误的程度，记为 $L(Y,f(x))$ .

（1）0-1损失

$L(Y,f(X)) =\begin{Bmatrix} 1,Y\neq f(X)\\ 0,Y=f(X) \end{Bmatrix}$

（2）平方损失

$L(Y,f(X)) = (Y-f(X))^2$

（3）绝对损失函数

$L(Y,f(X))=|Y-f(X)|$

（4）对数损失函数或对数似然损失函数

$L(Y,P(Y|X)) = -logP(Y|X)$

损失函数值越小，模型越好。损失函数期望：

$R_{exp}(f)=E_{p}[L(Y,f(x))]=\int_{x\times y}L(y,f(x))p(x,y)dxdy$

目标就是选择期望风险最小的模型。

由于联合分布律P(x,y)未知，故损失函数未知。

故选取训练数据集的平均损失称为经验风险(经验损失): $R_{exp}(f)=\frac{1}{n}\sum_{i=1}^{N}L(y_{i},f(x_{i}))$

根据大数定理，当N-> $\infty$ ,经验风险趋近于期望风险。但现实生活中样本数量有限，故利用经验风险预估期望风险不理想。

引入监督学习两个基本策略：经验风险最小化和结构风险最小化。

经验风险最小化：经验风险最小的模型是最优模型。

$\underset{f\in F }{min}\frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))$

F是假设空间。

极大似然估计就是经验风险最小化的例子。即损失函数是对数损失函数时，经验风险最小化等价于极大似然估计。

结构风险最小化：当样本容量很小时，容易出现“过拟合”现象。所以结构风险在经验风险上加上了正则化项或罚项。

结构风险=经验风险+正则化项(罚项)：

$R_{exp}(f)=\frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))+\lambda J(f)$

J(f)为模型复杂度，定义在假设空间F上的泛函。

经典例子：贝叶斯估计中的最大后验概率估计。

1.3.3 算法

算法指学习模型的具体计算方法。

1.4 模型评估与模型选择

设：学习到的模型是 $Y=\hat{f}(x)$ ,训练误差是模型 $Y=\hat{f}(x)$ 关于训练数据集的平均损失：

$R_{exp}(f)=\frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))$

N是训练样本容量。

但是在训练中也会出现过拟合现象，对原始数据的噪声过滤较少，使得训练的模型过拟合现象严重。

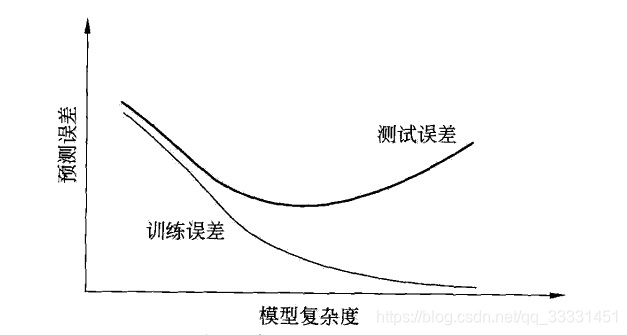
可以看到，当模型复杂度增大时，训练误差逐渐变小，直至为0。测试误差开始会减小，当达到一个最小值后，出现“过拟合”现象。下面有两种常用的模型选择方法：正则化与交叉验证。

1.5 正则化与交叉验证

1.5.1 正则化

正则化是结构风险最小化策略的实现，是在经验风险上加一个正则化项或罚项。正则化项是随模型复杂度单调递增。

$R_{exp}(f)=\frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))+\lambda J(f)$

正则化项： $\lambda J(f)$ ， $\lambda\geq0$ 为调整两者之间的关系的系数。

回归问题下的正则化，损失函数时平方项，正则化项可以是参数向量的L2的范数：

$L(w)=\frac{1}{N}\sum_{i=1}^{N}(f(x_{i};w)-y_{i})^2+\frac{\lambda}{2} ||w||^2$

||w||表示参数向量w的L2范数。

正则化的目的是选择经验风险与模型复杂度同时较小的模型。

1.5.2 交叉验证

模型选择将数据集分为三部分：训练集、验证集、测试集。验证集是用来进行模型的选择。

交叉验证就是为了选择好的模型。交叉验证的基本想法是：重复使用数据；把给定的数据进行切分，将切分的数据集组合为训练集组合为训练集与测试集。

交叉验证可分为：简单交叉验证、S折交叉验证、留一交叉验证。

1.6 泛化能力

泛化误差定义：根据学到的模型 $\hat{f}$ ，对未知的数据集进行预测，得到的误差就是泛化误差。

$R_{exp}(\hat{f})=E_{p}[L(Y,\hat{f}(X))]=\int _{x\times y}L(y,\hat{f}(x))P(x,y)dxdy$

学习方法的泛化能力分析通过研究误差的概率上界进行，就是泛化误差上界。

$R(f)\leqslant \hat{R}(f)+\epsilon (d,N,\delta )$

其中， $\epsilon (d,N,\delta )=\sqrt{\frac{1}{2N}(logd+log\frac{1}{\delta})}$

上不等式左端R(f)是泛化误差。右端为泛化误差上界。 $f\in F,f_{N}=arg \underset{f\in F}{min}\hat{R}(f)$

右端第一项是训练误差，训练误差越小，泛化误差越小。第二项是N的单调递减函数，当N趋近于无穷时，该项趋近于0。N为样本数量。证明过程在此不做证明。

1.7 生成模型与判别模型

监督学习的任务就是学习一个模型，应用这个模型，对给定的输入预测相应的输出。

根据监督学习方法可以分为：生成方法和判别方法。

生成方法由联合概率分布P(X,Y)，求出条件概率分布P(Y|X)作为预测的模型。如：朴素贝叶斯法和隐马尔可夫模型(HMM)

判别方法由数据直接学习决策函数f(x)或者条件概率分布P(Y|X)作为预测的模型，即判别模型。如：KNN，感知机、决策树、逻辑斯蒂回归模型、最大熵模型、支持向量机、提升方法和条件随机场。

特点：生成方法可以还原出联合概率分布P(X,Y),判别方法不能；生成方法学习收敛速度更快，即当样本容量增加时，学到的模型可以更加快的收敛于真实模型；当存在隐变量时，仍可以用生成学习，判别方法就不能用了。

判别方法直接学习的是条件概率P(Y|X)或决策函数，直接面对预测，往往学习的准确率更高。

1.8 分类问题

分类问题包含学习和分类两个过程。如：KNN、感知机、朴素贝叶斯、决策树、决策列表、逻辑斯谛回归模型、SVM、提升方法、贝叶斯网络、神经网络、Winnow等。

1.9 标注问题

标注也是监督学习的一个问题，是分类问题的推广。

训练数据集：

$T={{(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{N},y_{N})}}$

输入观测序列： $x_{i}=(x_{i}^{1},x_{i}^{2},...,x_{i}^{n})^{T}$ ,输出标记序列： $y_{i}=(y_{i}^{1},y_{i}^{2},...,y_{i}^{n})^{T}$

条件概率分布： $P(Y^{(1)},Y^{(2)},...,Y^{(n)}|X^{(1)},X^{(2)},...,X^{(n)})$

简而言之，就是对样本数据中的信息进行标注分类。

1.10 回归问题

回归用于预测输入变量和输出变量之间的关系。回归模型表示输入变量到输出变量之间的映射函数。回归问题等价于函数拟合。

思维导图

第1章统计学习方法导图

后记

由于是第一次写优快云博客，所以写的较为“僵硬”，但是感觉写完之后印象深刻，还是对的起自己所用的时间。

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。