1.激活函数
作用:激活函数的作用是实现线性函数的去线性
原理:将神经网络最后一层隐藏层的输出都经过一个非线性函数,那么整个神经网络就是一个非线性函数了。
用法:特征矩阵*权重矩阵+偏置矩阵
数学定义:
TensorFlow实现:
a = tf.nn.relu(tf.matmul(x, x1) + biases1)
y = tf.nn.relu(tf.matmul(a, x2) + biases2)
2.常见非线性函数:
ReLU函数:
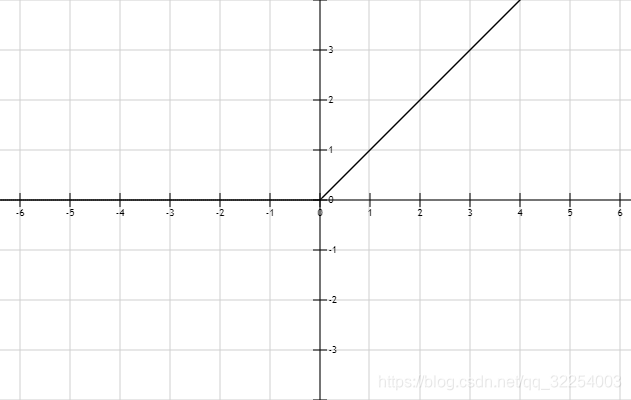
sigmoid函数:
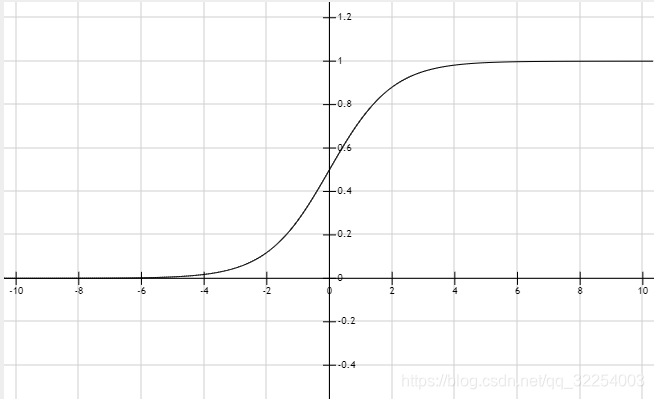
tanh函数:
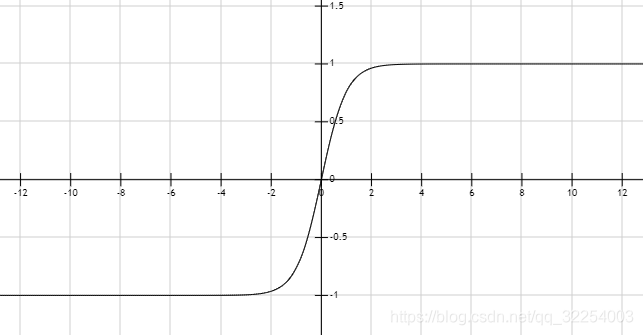
作用:激活函数的作用是实现线性函数的去线性
原理:将神经网络最后一层隐藏层的输出都经过一个非线性函数,那么整个神经网络就是一个非线性函数了。
用法:特征矩阵*权重矩阵+偏置矩阵
数学定义:
TensorFlow实现:
a = tf.nn.relu(tf.matmul(x, x1) + biases1)
y = tf.nn.relu(tf.matmul(a, x2) + biases2)
ReLU函数:

sigmoid函数:

tanh函数:


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


