概率论第6记：随机变量的数字特征之期望值

从现在开始，开始接触到神经网络里面经常遇到的一些概念：期望值、方差、协方差等。一个一个来
所谓期望值，就是我们所说的算术平均值，如果还是不明白，那么举例如下：
一书店购入一批（共N本）次年的挂历.在当年11月底前售出可盈利10元/本，当年12月份以折扣价售出盈利6元/本，次年1月份以进货价售出盈利0元/本，次年2月份作为废纸售出亏本9.7元/本.售出一本挂历盈利X（元）是一个随机变量，据往年经验知X的分布律如下：

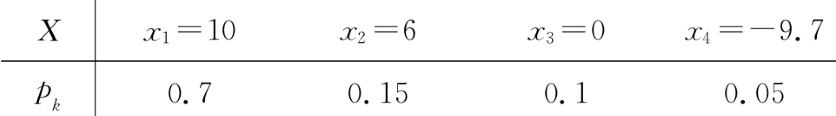
问：预期平均一本挂历能盈利多少？
解：如果书店分别在当年11月底前、12月份、次年1月份、次年2月份售出n₁，n₂，n₃，n₄本，n₁+n₂+n₃+n₄=N，那么平均一本盈利为然而这个数事先并不知道，要等到次年2月份结算时才能知道.注意到这里n_k/N是事件{X=xk}发生的频率.当N充分大时n_k/N在某种意义下接近于事件{X=x_k}的概率p_k，于是平均一本挂历盈利为

这就是说，书店购入一大批挂历，可以预期平均一本挂历盈利7.415元左右.
这里的7.415就是算数平均值，也就是所谓的期望值。
因此我们可以定义期望值：
设离散型随机变量X具有分布律P{X=x_k}=p_k（k=1，2，…），且级数${\sum }_{k=1}^{\infty }{x}_k{p}_k$绝对收敛；设连续型随机随机变量X具有概率密度f（x），且积分${\int }_{-\infty }^{\infty }xf\left(x\right)dx$绝对收敛。随机变量X的数学期望记为E（X），定义为

数学期望简称为期望，或称为均值.
再举一个稍微复杂一些的例子：
设X服从泊松Poisson分布，其分布律（离散型的分布律就是连续型的概率密度）为：P{X=k}=$\frac{{\lambda }^k{e}^{-\lambda }}{k!}$
则

后面的求和=$e^{\lambda }$，因为是$e^{\lambda }$的泰克展开式
期望值具有如下运算特征：
（1）设c是常数，则有E（c）=c.
（2）设c是常数，X是随机变量，则有E（cX）=cE（X）.
（3）设X，Y是两个任意的随机变量，则有E（X+Y）=E（X）+E（Y）.这一性质可以推广到有限个随机变量之和的情况.
（4）设X，Y是两个相互独立的随机变量，则有E（XY）=E（X）E（Y）.