最大奖励强化学习：非累积奖励判断标准

最新推荐文章于 2025-07-03 10:47:28 发布

翻译最新推荐文章于 2025-07-03 10:47:28 发布 · 4k 阅读

强化学习同时被 2 个专栏收录

19 篇文章

订阅专栏

文献

12 篇文章

订阅专栏

提出最大奖励强化学习，解决累积奖励模型不足，适用于最优停止问题，提高学习效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Title: Maximum reward reinforcement learning: A non-cumulative reward criterion
Author: K.H. Quah, Chai Quek Nanyang Technological University
Journal: Expert Systems with Applications 31 (2006) 351–359

评价：这篇论文是关于强化学习应用于最优停止问题的。作者提出回报函数采用最大奖励，并使用资格迹。本文的研究并不能让人满意，主要还是应用的问题太简单，对于复杂非线性问题的应用效果存疑。

读后感：这是一篇二区SCI，档次高真不见得是工作突出。创新点设计并无亮点，第三节的例子真是像说废话一样。但是客观讲二区没大毛病，该有的都有了。

摘要

文献中提出的现有强化学习范式由两个性能判断标准指导，即：预期累积奖励和平均奖励。这两个判断标准都假设奖励本身存在累积或可加性。然而，在某些情况下，这种固有的奖励累积并不是必然的。本文介绍了两种可能的场景。第一个问题是学习的最优策略远离存在的更近的次优策略。由于累积较低奖励的影响，累积奖励范型收敛较慢，并且要花费时间消除次优策略的影响。第二种情况涉及近似最优停止问题的收益的上限值。收益本质上是非累积的，因此累积奖励范型不适用于解决此问题。因此，在这些应用环境中需要非累积奖励强化学习范型。本文提出了一个最大奖励标准，所得到的具有该学习标准的强化学习模型被称为最大奖励强化学习。最大奖励强化学习考虑了非累积奖励问题的学习，其中代理展示了针对状态空间中最大奖励的最大奖励导向行为。在这种学习范式中忽略了导致次优策略的中级较低奖励。随后使用FITSK-RL模型对最大奖励强化学习进行建模。最后，该模型应用于具有非累积奖励性质的最佳停止问题，并且在与其他模型进行基准测试时其性能是令人鼓舞的。

1.简介

强化学习是一种试错法学习方法，其中代理尝试从长期接收的反馈中探索并最大化数值状态值。代理遵循的过程被建模为马尔可夫决策过程（MDP）。在MDP背景下，两个最充分研究的最优性标准是预期的累积奖励和平均奖励标准（Puterman，1994）。预期的累积奖励标准已被用作强化学习研究中的事实客观尺度（Bertsekas，＆Tsitsiklis，1996; Kaelbling，Littman＆Moore，1996; Rummery＆Niranjan，1994; Sutton，1984,1988; Sutton＆Barto， 1998; Watkins，1989）。该标准采用一种技术以指数方式对未来奖励进行折扣，使得近期奖励比远期奖励更有价值。然而，一些研究表明，预期的累积奖励标准不适合某些问题，特别是在未折现的奖励领域（Schwartz，1993）。已经提出了一些基于平均奖励标准的强化学习方法来解决未折现的奖励强化学习问题（Mahadevan，1996; Schwartz，1993; Tadepalli＆Ok 1998）。在本质上，两类方法都采用某种形式的累积奖励标准;前者采用奖励折扣方式，使得他们的无限累积奖励是有限的，而后者采用奖励平均法，使短期和长期奖励无法区分。

然而，一个核心问题是这种累积奖励制定是否是所有学习环境中的明确必要条件的问题。有没有问题累积奖励的表述是不必要的，也是不合理的？本文讨论了两种可能的情景，其中要避免累积奖励制定以获得优异的学习效果。这在第3节和第4节中得到了证明。在第3节中，讨论了（Mahadevan，1996）的两个循环任务。其中一个周期导致次优政策而另一个周期导致最优政策，但最优政策的回报更远。因此，学习的重点是如何在寻找最优策略时绕过次优策略。经典的Q学习（Watkins，1989）被证明会受到这个问题的困扰，因为它被次优政策拖累，导致它转向更好的政策。在第4节中，讨论了金融衍生品定价产生的最佳停止问题（Tsitsiklis和Van Roy，1999）。这是累积奖励制定不合理的情况。另一方面，该问题涉及找到每个州的支付值的上限，其是非累积方式的预期折扣最大奖励的函数。此外，折扣奖励在该领域中是重要的，因为贴现操作代表对金融定价漂移率的未来奖励的补偿。这与（Schwartz，1993）提出的一项相反的论点相反，即奖励的折扣并不一定重要。有了这些，提出了一个具有非累积最大奖励标准的强化学习公式，以适应这些任务的学习需求。

最大奖励强化学习代理表现出最大奖励导向行为。它试图寻找导致最大奖励的策略;无论沿着路径的中间较低的奖励。这使得它对问题领域中次优策略的存在具有更高的免疫力，例如第3节中的两个周期问题。此外，最大奖励学习被证明在近似的金融定价背景的未来收益中是有效的。学习系统表现出用最大奖励公式近似最高值的渐近行为，这将在第4节中讨论。

本文的结构如下。第2节描述了最大奖励强化学习及其更新公式的一般表述，作为早期提出的通用强化学习框架的模块化设计的一部分 - （Quah＆Quek，提交出版）。第3节研究使用双周期任务的最大奖励强化学习的学习行为，并与两个现有的强化学习模型进行比较。第4节将建议的最大奖励强化学习及其通用学习框架应用于金融衍生品定价背景下的最优停止问题。第5节总结了本文。

2.3 映射到通用强化学习框架

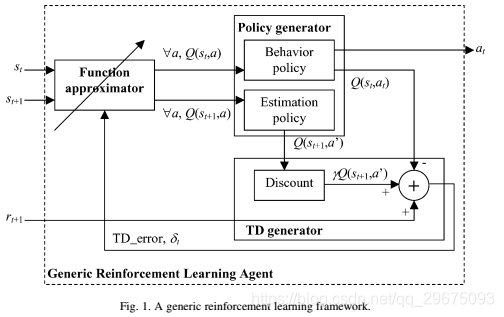
本小节将最大奖励强化学习更新公式（公式（2.15））扩展到（Quah＆Quek，提交出版）中提出的通用强化学习框架。框架的通用代理的框图如图1所示。

通用代理采用模块化设计，具有三个模块;即：函数逼近器，策略生成器和时间差分（TD）生成器。函数逼近器模块基于状态信息预测值函数。策略生成器模块生成适当的操作和相应的操作值。 TD生成器模块随后基于增强信号，当前动作值和连续动作值来制定时间差分误差。因此，时间差分误差是反馈到函数逼近器模块以调整可调参数。具有这种模块化设计的两个动机是功能通用性或抽象性以及功能独立性。具有用于每个相应模块的通用功能使得框架能够被抽象地定义，并且因此可以容易地扩展到不同的强化学习模型，例如TD学习，SARSA学习或Q学习。此外，功能独立性确保模块彼此不紧密相关，因此单个模块的重新配置或实现不会影响其他模块的一般操作。本文的讨论仅限于以下范围; TD生成器模块正在被推广以包含最大奖励更新公式的学习。有关函数逼近器和策略生成器模块的定义，请参阅（Quah和Quek，已提交）。

TD生成器根据即时奖励，当前动作值和连续动作值估计来计算时间差分误差，如等式（2.16）所示。

公式中的TD误差公式。通过在策略生成器模块中采用不同的动作选择策略，可以很容易地将（2.17）或（2.18）映射到TD学习，SARSA学习或Q学习，如（Quah＆Quek，提交出版）中所示。此外，通过采用零阶FITSK模型（Quah＆Quek，提交出版）作为函数逼近模块，可以将最大奖励强化学习直接纳入FITSK-RL模型（Quah＆Quek，提交）。这使得值函数能够以系统的方式用线性逼近器（与可调参数成线性）有效地近似，并且可以扩展到用资格迹线公式学习（Sutton，1984）。有关制定FITSK-RL模型的技术细节，请参阅（Quah＆Quek，提交出版）。

3.与Q学习和R学习的比较

本节将提出的非累积，最大奖励强化学习与现有学习模型与固有的累积奖励强化学习模型进行比较，特别是Q学习（Watkins，1989）和R学习（Schwartz，1993）。 Q-learning是一种异策略，无模型的强化学习模型，并且通过折扣累积奖励被证明在控制任务学习中是有效的。用于Q学习的学习方程由方程（2.14）描述。。制定Q学习控制的基本思想是采用贪婪策略作为估计策略，同时使用非贪婪行为策略探索搜索空间。同样，R-learning是一种异策略，无模型的模型。然而，R学习的目的是基于无折扣的累积奖励值而不是方程（2.2）中描述的折扣累积奖励值来最大化性能。从时间t开始的过程的无折扣的累积奖励值显示在等式（3.1）中。

${\rho _t} = \mathop {\lim }\limits_{n \to \infty } \frac{1}{n}\sum\limits_{k = 0}^n {{r_{t + k + 1}}}$ （3.1）
其中 $\rho_t$ 是时间t的平均无折扣累积奖励。（Schwartz，1993）证明，如果一个策略产生遍历性的马尔可夫链，那个遍历性的马尔可夫链中所有状态的平均回报值是相同的（方程（3.2））。
$\rho = {\rho _t},\forall {s_t} \in {S_E}$ （3.2）

其中 $S_E$ 是遍历状态的集合。

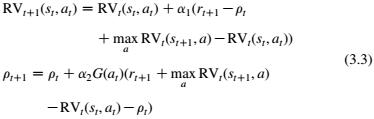
R学习的更新公式表示在方程（3.3）中。关于这些更新公式的合理性，请参阅（Schwartz，1993）。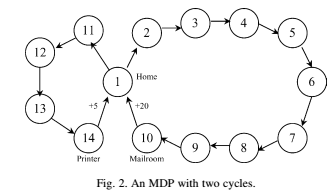

图2示出了来自（Mahadevan，1996）的示例，其是对MDP的状态1（Home）处的动作选择的两个周期马尔可夫决策过程（MDP）任务（Schwartz，1993）的改编。跟随该MDP的机器人在打印机房（状态14）接收从家到打印机房的行程的+5的奖励，并且接收+20的奖励以服务更远的邮件室（状态10）。学习模拟分别用于R学习（方程（3.3）），Q学习（方程（2.14））和QM学习（方程（2.15））。所有的学习率都设为0.2，所有的行为策略都是 $\varepsilon$ -greedy（Sutton，1998）， $\varepsilon =0.05$ 。

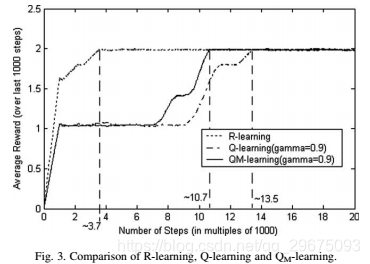
图3显示了R学习，Q学习和QM学习之间的性能比较。结果在5次独立运行中取平均值，每次运行由20,000个步骤组成。通过在过去的1000个步骤中累积的奖励的平均值来测量性能。最佳路径遵循1-2-3-4-5-6-7-8-9-10的循环，并且无限重复。因此，平均奖励值的最大值是2，并且通过对每个周期的最大奖励20，超过10个动作求平均得出。在达到最优策略之前，学习代理通常可以遵循次优策略，该策略遵循1-11-12-13-14的周期。该次优策略的平均奖励为1. Q学习和QM学习采用折扣率 $\gamma =0.9$ 。此MDP中的折扣率必须大于0.7579，以便选择为邮件收发室提供服务的策略。任何低于0.7579的折扣率都会导致11状态的价值高于状态2的价值。因此，为打印机房提供服务的策略看起来比服务于Mailroom的策略更有吸引力。 R学习在大约3700个步骤达到最优解，而QM学习和Q学习分别要10,700和13,500步达到最优解。

与无折扣公式中的R学习相比，具有折扣公式的学习倾向于收敛于次优解。然而，最大奖励QM学习比累积奖励Q学习略好。有关这种现象的原因将在下一次模拟中讨论。

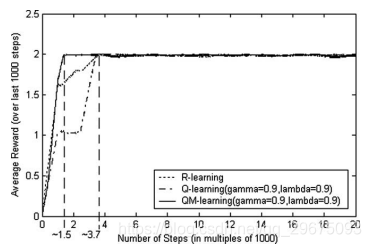
在图4中研究了R-learning在先前模拟中优于QM学习的原因。资格迹公式（Sutton，1984; Sutton＆Barto 1998）被引入到Q-learning和QM-learning中，具有大的迹 - 衰减参数， $\lambda =0.9$ 。这确保了学习代理一旦被非贪婪的探索性策略发现，他们的未来奖励就会明显。图4显示具有资格追踪的QM学习具有优于其他的QM学习。通过采用资格迹，QM学习比其他人更有远见。 QM学习在大约1500个步骤中收敛，而Q学习和R学习在大约3700个步骤中收敛。 QM学习在尽可能短的时间内收敛到最优策略，而不会受到次优策略的拖累。这与第2.2节中介绍的最大奖励代理的行为一致。代理将尝试发现导致最高奖励的最短路径，而不会过多地关注中间较低的奖励。然而，对于诸如Q学习或R学习之类的累积奖励模型，它们需要时间来消除较低奖励的影响和次优策略的影响。因此，这些累积奖励模型的收敛并不像非累积最大奖励模型那样直接。

4.金融衍生品定价中的最优停止问题

在关于平均奖励强化学习的原始论文中（Schwartz，1993），作者声称折扣奖励的原因之一是补偿未来奖励的比率，特别是在经济领域。（Tsitsiklis＆Van Roy，1999; Van Roy，1998）在金融衍生品定价中最优停止问题的研究中证明了这一点。然而，折扣累积奖励强化学习模型不能轻易解决问题。这是因为问题的目的是确定具有最高折扣非累积奖励的最佳停止状态。本节试图证明最大奖励强化学习的应用，以模拟这种金融衍生品定价问题。

4.1 问题的表述

最佳停止问题最初由（Van Roy，1998; Tsitsiklis，1999）提出，用于对外来衍生产品进行最优定价预测（Parsley，1997）。问题域是基于单个股票的每日价格的合约。当合同被行使时，收到的收益金额等于股票的当前价格除以100天前的价格。有关此问题的背景研究和详细信息，请参阅（Tsitsiklis，1999）。该问题的总结如下。

股票价格的过程是基于几何布朗运动模型生成的（Hull，1997）。股票价格的变化被建模为正态分布，漂移率为平均值，波动率为标准差，如公式（4.1）所述。

$\frac{{\Delta {p_t}}}{{{p_t}}} \sim \phi \left( {\mu \Delta t,\sigma \sqrt {\Delta t} } \right)$ （4.1）

如果价格是每天计算的，则时间间隔为1，并且Eq（4.1）被简化为方程式1中描述的更新方程（4.2）。
${p_{t + 1}} = {p_t}\left( {1 + \mu + \sigma \phi \left( {0,1} \right)} \right)$ （4.2）

这个问题考虑到每日波动率为0.02，年利率为10％;通过将利率除以市场开放日数（w250天），漂移率为0.0004。因此，每日价格根据Eq （4.3）更新。

${p_{t + 1}} = {p_t}\left( {1.0004 + 0.02 \phi \left( {0,1} \right)} \right)$ （4.3）
其中 $t\geq -100$ 。

在特定离散时间t可用于学习代理的信息是向量，如下所述，

如果合同在时间t终止，则可以获得回报。
因此，稍后收到的奖励是信息矢量的最后一个部分， $r_{t+1}=x_t(100)$ 。然后在时间t的合同价值由公式给出。（4.4）。

折扣率由 $\gamma = e^{-\mu}$ 给出。如果t *是最佳停止时间，那么合约的最优值由等式1描述。（4.5）。

4.2。学习模型的制定和结果
问题的状态是基于以下原理构建的。如果在过去100天内股价大幅下跌和股价回升，那么合约可能会持有一段时间以获得潜在的未来利益（Tsitsiklis，1999; Van Roy，1998）。因此，最重要的信息取决于当前股票价格和过去100天的最低股票价格。有了这个基本原理，状态信息的构造如公式（4.6）所示。第一个状态维度表示当前股票价格的比例增量。第二个状态维度表示当前股票价格与过去100天最低股票价格的比例增量之差。

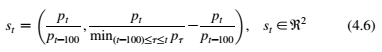
在模拟试验中，由于训练迭代次数总是有限的，因此在预期折扣支付的集合中存在最大值，并且该最大值也是集合的上限（方程（4.7））。

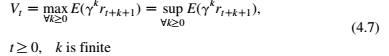
式（4.7）相当于Eq（2.6），这是最大奖励强化学习的价值函数。因此，这个最优停止问题可以用最大奖励强化学习TDM学习来近似，其中更新误差公式如公式1所示。（2.15）。

在此模拟中，最优值函数与FITSK-RL模型近似。 FITSK-RL模型由零阶FITSK作为函数逼近器组成。学习参数如表1所示。

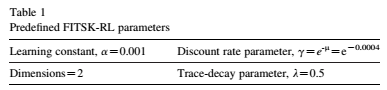
第一维和第二维表示为s（1）和s（2），其使用等式（4.6）来计算。两个状态维度的输入范围分别为 $s(1)\in(0.5,2.0)$ 和 $s(2)\in(0.0,0.6)$ 。两个维度的预分配隶属函数数量为5和3。要调整的参数总数为 $5\times 3=15$ 。所有初始可调参数都设置为零。学习重复500,000,000次。来自模型输出的近似值函数绘制在图5中。

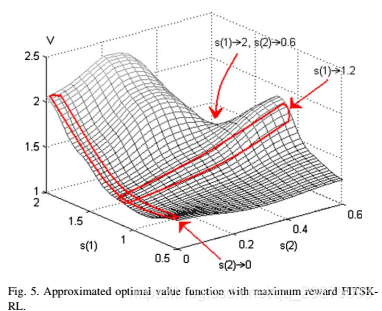
图5示出了在学习迭代之后具有所提出的最大奖励FITSK-RL模型的近似最优值函数的表面图。两个状态尺寸用X-Y轴表示，近似最佳值函数用Z轴表示。当当前股票价格接近过去100个价格（s（2）/ 0）的底部时，那么获得更好的进一步收益的机会并不大，因此期望收益率降低。当当前股票价格在s（1）中产生约1.2的增长时，支付的预期与s（2）成比例地增加。增加s（2）意味着在过去100天内存在更大的衰退和复苏，并且可能应该等待一段时间以获得更高的收益。右上角的区域（s（1）/2.0,s(2)/0.6）很少遇到（见图5），因此由于缺乏训练，他们学到的最佳值低于预期例子。但是，当发生这种情况时，该过程将立即终止，以从这些状态中获得高收益。这是因为获得任何潜在的更高回报的可能性比当前更小。

从中表示近似的最优值函数，FITSK-RL为 $\widetilde{V}(S_t)$ ，则停止时间 $\widetilde{\tau}$ 由式（4.8）计算。这类似于（Tsitsiklis，1999）定义的终止标准，它被证明是最佳停止时间。

（4.8）

对应于近似最佳值函数的预期奖励通过平均在50,000个独立轨迹上收集的奖励来估计，并且根据等式1终止。（4.8）。结果列于表2中。根据此停止标准计算的预期回报为1.289127，该样本均值的估计标准偏差为0.002856。阈值策略的预期奖励为1.238; （Tsitsiklis，1999）公式的近似最优值函数和1.282（样本均值的标准偏差为0.0022）。因此，最大奖励FITSK-RL模型的预期收益略好于Tsitsiklis的，后者为0.007127。预期奖励在数值上比阈值策略好0.051127。这意味着由最大奖励FITSK-RL模型确定的策略的最优定价比阈值策略好5％，并且比Tsitsiklis好大约1％。

4.3 讨论

在关于无折扣奖励问题的平均奖励强化学习的原始论文中，作者声称使用奖励折扣来补偿利率是不合理的（Schwartz，1993）。然而，本文研究的金融衍生品定价中的最优停止问题表明了相反的情况。 $e^{-\mu}$ 会对折扣进行补偿，以补偿合约价值未来可能的增量，以便未来的价值与当前价值一起考虑。另一方面，折扣累积奖励强化学习不适用于此问题。这是因为问题的目的是为每个状态寻找最高的预期奖励。有了这个，非累积，折扣，最大奖励强化学习公式被证明可直接应用于解决这个问题。

FITSK-RL模型在2.3节中轻松融入了最大奖励强化学习方法。使用最大奖励FITSK-RL模型模拟本节中的问题。本节中提出的公式与（Tsitsiklis，1999）中提出的公式略有不同。他们用100个状态维度来表示问题，以证明其局部基函数近似的良好缩放。本文中的公式将状态维度减小到2，这样学习结果可以很容易地可视化和检查（如图5所示）。这提高了学习结果的可解释性。此外，FITSK-RL模型的操作是系统定义的，而不是手动生成的局部基函数近似方法（Tsitsiklis，1999）。具有2个状态维度的最大奖励FITSK-RL模型的预期收益略微优于具有100个状态维度的现有方法。这表明了Eq（4.6）中的状态定义具有两个维度可以充分地为学习系统提供足够的信息。这是对现有方法的建模复杂性的重大改进。

5.结论
本文提出了一种新的最大奖励标准作为强化学习的目标。最后的奖励标准随后从马尔可夫决策过程的角度被纳入强化学习更新公式。随后，最大奖励强化学习被映射到通用强化学习框架，以解决这种新学习范式的建模问题。

最大奖励强化学习的独特特征是学习代理的非累积的，最大的奖励导向行为，而不是通常的累积奖励导向行为。它试图寻找导致最大奖励的策略，无论中间较低的奖励如何。这使其对次优策略的存在具有更高的免疫力。第3节中的示例对此进行了演示，其中最大奖励代理在最短时间内建立了与最优策略的收敛。然而，具有潜在的累积奖励导向行为的其他代理正受到次优策略和较低奖励的拖累。结果，他们遭遇较慢的收敛到最优策略。

第4节演示了最大奖励强化学习的成功应用，以渐近逼近最优停止问题中的支付值的上限。已采用2.3节中提出的最大奖励FITSK-RL模型来解决这个问题。使用通常的累积奖励强化学习范例无法有效解决这个问题，因为潜在的支付价值是非累积的。尽管将问题减少到两态维数问题，使用FITSK-RL模型的近似结果略微优于具有100个状态维度的原始公式（Tsitsiklis和Van Roy，1999）。此外，这提高了学习结果的可解释性并降低了问题的建模复杂性。可视化近似结果，以便可以容易地检查结果的基本原理。对于问题的原始公式，这是不可能的，因为状态维度太大并且难以深入了解手动定义的局部基函数的学习结果。然而，这可以通过FITSK-RL模型实现，因为操作是系统定义的，并且状态尺寸很小。

总之，最大奖励强化学习方法被提议作为一种可能的新学习范式，以表现出具有奖励价值的潜在非累积性质的问题的优越表现。提供了示例和模拟来说明这一点。通过将其映射到通用强化学习框架来解决最大奖励强化学习的建模问题。然而，最大奖励强化学习的理论研究仍处于起步阶段，特别是从最优控制角度来看。由线性函数逼近器产生的最大奖励强化学习的收敛性尚未建立。可能会从Tsitsiklis的论文（Tsitsiklis和Van Roy，1997,1999）中扩展出一些可能的收敛结果相似性，这证明需要进一步研究。与敏感折扣最优性标准的关系（Mahadevan，1996; Puterman，1994）尚未研究过，值得进一步研究。