机器学习中的分类模型和回归模型

机器学习中的分类模型

1.KNN

2.感知机

3.朴素贝叶斯法

4.决策树

5.逻辑斯谛回归模型

6.SVM

7.AdaBoost

8.随机森林

9.贝叶斯网络

10.神经网络

机器学习中的回归模型

1.线性回归

2.多项式回归

3.岭回归(Ridge Regression)

岭回归(英文名：ridge regression, Tikhonov regularization)是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。

3.1 为什么会有岭回归？

总结起来看，主要有两个原因：
①当样本少于特征（数据点少于变量个数），输入数据的矩阵x非满秩矩阵（即|xTx|≈0），求逆的时候会出问题；

②当样本之间存在共线性（也就是强相关性），普通的最小二乘法得到到的回归系数估计得方差很大，会导致估计值很不稳定；

岭回归是对最小二乘回归的一种补充，它损失了无偏性，来换取高的数值稳定性，从而得到较高的计算精度。

4.Lasso回归

Lasso回归和岭回归类似，也是在损失函数后面加上正则化项，不过不同于岭回归，Lasso回归添加的正则项是所有参数w的绝对值之和，也即是L1范数；而岭回归添加的则是所有参数的平方和，也即是L2范数。

5.弹性网络

弹性网络是结合了岭回归和Lasso回归，由两者加权平均所得。据介绍这种方法在特征数大于训练集样本数或有些特征之间高度相关时比Lasso更加稳定。其代价函数为：

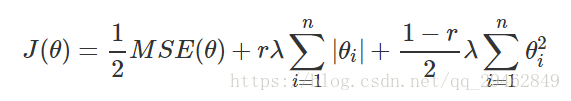
6.GBDT

7.CART

8.XGBoost