算法分析：冒泡

求和

符号是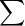，一般用法是，表示1+...+100， 表示 2*1 + ...... + 2*100

 

分析的维度

主要是有

1. 比较次数（最坏情况，最好情况，平均情况）
2. 交换次数（最坏，最好， 平均）
3. 辅助空间（最坏，最好，平均）
4. 为了方便，很多分析会把一次比较和一次交换看做耗时相同的一次操作。不过在算法执行过程中，交换次数总是少于（甚至远远少于）比较次数。所以有的分析方法只关注比较次数。

冒泡排序（选择排序）

第一趟排序要经历： 5，2比较； 2，3比较，2，3互换； 2，4比较，2,4互换； 2，1比较。

4次比较和2次互换。整个过程没有使用辅助空间。

 

经过总结可以得到：

对于长度为N数组，

第一趟排序，需要比较N-1次，在最优的情况下，需要互换0次；最坏的情况下需要互换N-1次

第二趟排序，需要比较N-2次，在最优的情况下，需要互换0次；最坏的情况下需要互换N-2次

最后一趟是第N-1趟，需要比较1次。最优情况，交换0次；最坏情况交换1次。

整个排序不需要辅助空间。

 

因此，一共需要比较次，最优的情况下，还需要交换0次‘；最坏的情况下，需要交换次。

因此冒泡排序的操作次数在与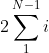之间。

冒泡排序是O(n^2)的复杂度

 

冒泡排序平均操作次数

冒泡排序中，比较次数是固定的

平均交换次数则是 (最好 + 最坏 ) /2 

因此，冒泡排序的平均操作次数是  

 

插入排序

public class InsertSort {

	private int[] data = {32, 23, 35, 1, 355, 2331, 87, 98, 800, 37, 32, 32, 37, 32, 37};

	public void sort() {
		int length = data.length;
		for (int i = 0; i < length; i++) {
			int j;
			for (j = i; j >0; j--) { // 插入元素
				if (data[j] < data[j-1]) { // 从右往左比较，交换
					int tmp = data[j];
					data[j] = data[j-1];
					data[j-1] = tmp;
				}
			}
		}
	}
	
	public void print() {
		System.out.println(Arrays.toString(data));
	}
	
	public static void main(String[] args) {
		InsertSort sort = new InsertSort();
		sort.sort();
		sort.print();
	}
}

分析

与冒泡排序是一样的。