归并排序

package test;
import java.util.Arrays;
public class MergeSort {
private static int[] DUMMY = new int[]{3, 2, 5, 7, 11, 4, 6, 9};
private int[] data;
public MergeSort() {
this(DUMMY);
}
public MergeSort(int[] data) {
this.data = data;
}
/**
* 将两个有序数组合并;左边的数组从start到middle, 右边的数组从middle + 1 到 end
* @param start
* @param middle
* @param end
*/
public void mergeSort(int start, int middle, int end) {
int[] tmp = Arrays.copyOfRange(data, start, end + 1);
int refIndex = start;
int left = start - refIndex, _refMiddle = middle - refIndex;
int right = _refMiddle + 1;
int _refEnd = end - refIndex;
int count = 0;
while (left <= _refMiddle || right <= _refEnd) {
int nextValue;
if (left > _refMiddle) { // 左边已经排完了
nextValue = tmp[right];
right ++;
} else if (right > _refEnd) { // 右边已经排完了
nextValue = tmp[left];
left++;
} else { // 都没排完
if (tmp[left] <= tmp[right]) {
nextValue = tmp[left];
left++;
} else {
nextValue = tmp[right];
right++;
}
}
data[count + refIndex] = nextValue;
count++;
}
}
public int[] sort() {
sort(0, this.data.length - 1);
return this.data;
}
/**
* 让data中的部分数据有序
*
* @param start , 数据index起
* @param end, 数据index止
*/
private void sort(int start, int end) {
if (start == end) {
return;
}
int middle = getMiddle(start, end);
sort(start, middle); // 先让左半边有序
sort(middle + 1, end); // 再让右半边有序
mergeSort(start, middle, end); // 合并
}
/**
* 获取start 和 end中间位置
* 举例: (4,5) -> 4; (0, 3) -> 1; (0, 2) -> 1
* @param start
* @param end
* @return
*/
int getMiddle(int start, int end) {
return (int)Math.floor(((float)end + start) / 2);
}
public void print() {
System.out.println(Arrays.toString(data));
}
public static void main(String[] args) {
MergeSort ms = new MergeSort(new int[]{3, 2, 5, 7, 11, 4, 6, 9});
ms.sort();
ms.print();
}
}
分析sort函数的复杂度,设长度为n的数组,sort函数复杂度为f(n);
sort函数的主要操作是3步:
-
让左半边有序,sort(0, n/2);
- 让右半边有序,sort(n/2, n);
- 合并左半边和右半边,mergeSort函数
因此 f(n) = f(n/2) + f(n/2) + O(mergeSort(n)) = 2f(n/2) + O(mergeSort(n));
先分析mergeSort(n)的复杂度。
mergeSort(n)需要长度为n的辅助空间。
只考虑比较次数,维度为:最好,最好,平均
分析发现任何情况下,mergesort函数的比较次数都是n( while循环的次数是n,而每次都有比较)
sort函数复杂度
f(n) = 2f(n/2) + n = 2[ 2*f(n/4) + (n/2) ] + n = 4f(n/4) + 2n
归纳总结可以得到
令m = n,公式可变为:
而f(1) = 0,所以
综上所述,归并排序在最坏的情况下是O(n * logn)复杂度的算法,需要使用n个辅助空间(假设排序没有使用多线程,整个程序最多只会使用n个辅助空间)
别人的分析思路
看上去跟自己的差不多,终于我也掌握了算法分析了/(ㄒoㄒ)/~~
下面文字中的O(1) 表示计算middle的复杂度。
最后补一张x^2 与 x* logx 函数的对比图
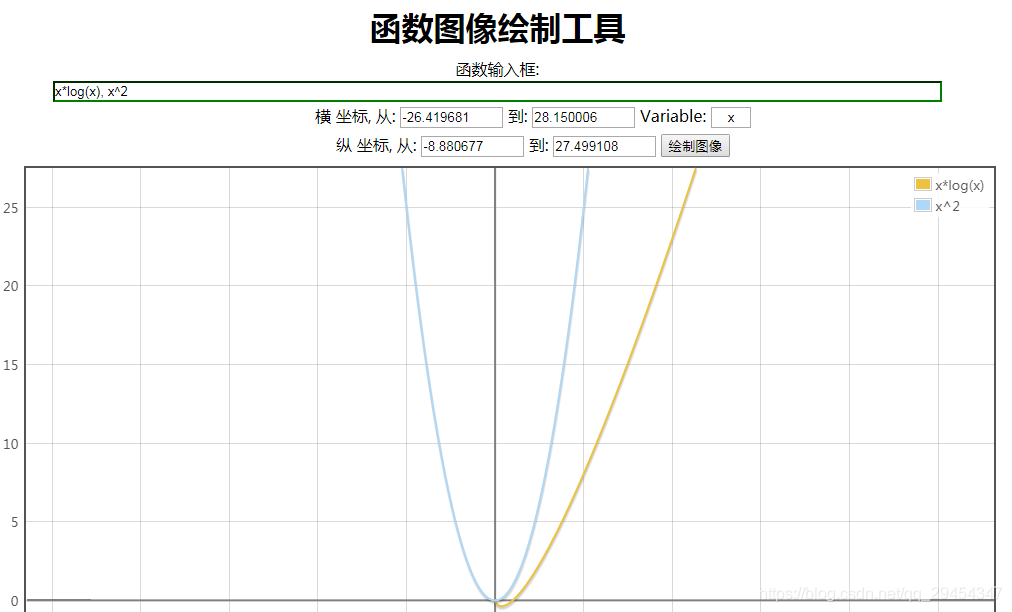







 本文详细分析了归并排序的sort函数复杂度,通过递归解析得出f(n) = 2f(n/2) + n,最终证明在最坏情况下归并排序的时间复杂度为O(n * logn),并指出需要n个辅助空间。此外,文中还提及了归并排序与其他算法复杂度的对比。
本文详细分析了归并排序的sort函数复杂度,通过递归解析得出f(n) = 2f(n/2) + n,最终证明在最坏情况下归并排序的时间复杂度为O(n * logn),并指出需要n个辅助空间。此外,文中还提及了归并排序与其他算法复杂度的对比。

















 1280
1280

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








