一、KNN和K-Means的区别?
区别
- KNN是一种监督学习算法,解决分类问题,而K-Means是非监督学习算法,解决聚类问题。
- KNN是人为选定k,含义是考察k个最近的样本,决定未知样本的所属分类,没有明显的训练过程。
- K-Means也是人为选定k,含义是k个聚类中心,计算样本到聚类中心的距离,得到初步的聚类结果,再由聚类结果更新聚类中心,迭代直至聚类中心不再变化为止。
相似点
- k值得选取会影响到分类/聚类结果。
- 都利用到了最近邻的思想(NN,Nears Neighbor)。
二、KNN的三要素是什么并解释?
-
K值的选取。
如下图所示,绿色圆形未知样本的分类与k值得选取密切相关。默认未知样本属于多数样本规则的前提下,当k选3,时结果为三角形,当k取5时,结果为正方形。
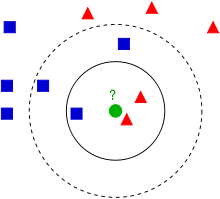
k值的选择还影响到模型的复杂度,k越小模型越复杂,k越大模型越简单。考虑极端情况,k选择整个数据集,如果用多数表决法,距离都不用算,未知样本一定属于占比最多的那类样本,模型就简单,因为每次结果都一样的。 -
距离的度量。
即采用什么样的距离度量标准,因为不同的距离计算公式,会决定未知样本最近的样本是哪些,进而影响到最终的分类结果。常见的距离度量标准
欧式距离
空间中有两个点A(x1,y1) B(x2,y2),距离d(A, B)=sqrt((x1-x2)^2 + (y1-y2)^2)。曼哈顿距离
空间中有两个点A(x1,y1) B(x2,y2),距离d(A, B)=|x1−x2|+|y1−y2|。 -
分类决策规则的选择
k值选好了,距离算出来了,怎么决定未知样本的分类呢?
默认的分类决策规则是多数表决法,就是前面用到的,谁多,未知样本就是谁那一类的。所谓近朱者赤近墨者黑。
有人可能会觉得这个规则不合理,直观上觉得绿色圆就应该属于三角形,因为图里那两个三角形离它太近了。所以又有新的分类决策规则:
加权多数表决法。
也就是说,不光考虑数量,还得考虑距离,距离近的样本获得的权重大,影响就大,远的样本权重小,影响就小。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








