统计学习方法 EM算法的一个例子

• 参考《统计学习方法》第九章

        三硬币模型 假设有3枚硬币，分别记作A,B,C.这些硬币正面出现的概率分别是π，p和q·进行如下掷硬币试验：先掷硬币A,根据其结果选出硬币B或硬币C,正面选硬币B,反面选硬币C:然后掷选出的硬币，掷硬币的结果，出现正面记作1，出现反面记作0：独立地重复n次试验（这里，n=10),观测结果如下：

1,1,0,1,0,0,1,0,1,1

        假设只能观测到掷硬币的结果，不能观测掷硬币的过程.问如何估计三硬币正面出现的概率，即三硬币模型的参数。题中一些信息我们可以用下图来表示。

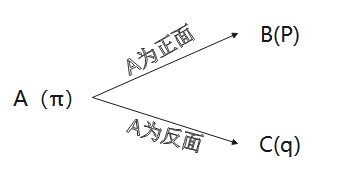
        解：设随机变量y是观测变量，表示一次试验观测的结果是1或0：随机变量z是隐变量，表示未观测到的掷硬币A的结果。那么

这是观测为正面的情况，同样的可以得到反面的情况，因此，这个模型可以写作