梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
梯度
函数:z=f(x,y)z=f(x,y)z=f(x,y) 在平面域内具有连续的一阶偏导数,对于其中每一个点 P(x,y)P(x,y)P(x,y)都有向量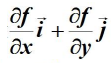
,则其称为函数在点P的梯度。

只有当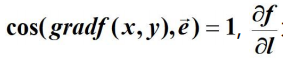
,才有最大值。
函数在某点的梯度是一个向量,它的方向与方向导数最大值取得的方向一致。 其大小正好是最大的方向导数
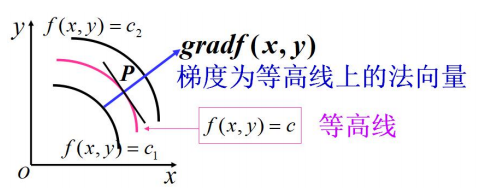
例
$设u=xyz+z^2+5,求grand $ u,并求在点u,并求在点u,并求在点M(0,1,-1)处方向导数的最大(小)值。$
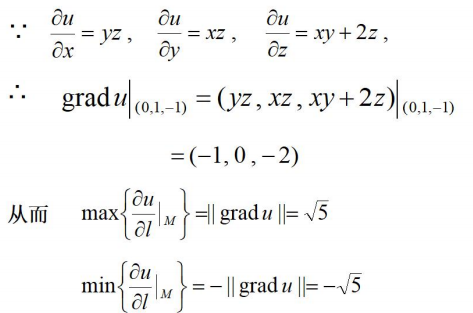





 本文介绍了高等数学中梯度的概念,它是一个向量,表示函数在某点沿其方向导数最大,变化最快。梯度的方向与最大方向导数方向一致,大小等于最大方向导数的模。举例说明了如何求解函数的梯度及在特定点的方向导数最大值。
本文介绍了高等数学中梯度的概念,它是一个向量,表示函数在某点沿其方向导数最大,变化最快。梯度的方向与最大方向导数方向一致,大小等于最大方向导数的模。举例说明了如何求解函数的梯度及在特定点的方向导数最大值。

















 2130
2130

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










