《数字滤波器的MATLAB与FPGA实现》学习笔记第四章 FIR滤波器的FPGA设计与实现

Bahair_

已于 2025-02-21 12:09:06 修改

阅读量1k

点赞数 15

分类专栏：电赛文章标签： fpga开发嵌入式硬件

于 2025-02-21 12:06:47 首次发布

本文链接：https://blog.youkuaiyun.com/qq_26923297/article/details/145746457

版权

参考文献：《数字滤波器的MATLAB与FPGA实现—Altera Verilog版》[杜勇编著] 2015年版

一、FIR滤波器的理论

$y(n)=\sum _{k=0}^{k=M}b_{n-k}x_{n-k}$

$h(n)=\sum_{k=0}^{k=M}b(n-k)$

当FIR滤波器的系数对称时，通带内满足线性相位。系数奇对称相比于系数偶对称多了90°的相移。这种在所有频率上都产生90°相移的变换称为正交变换，这种网络称为正交变换网络
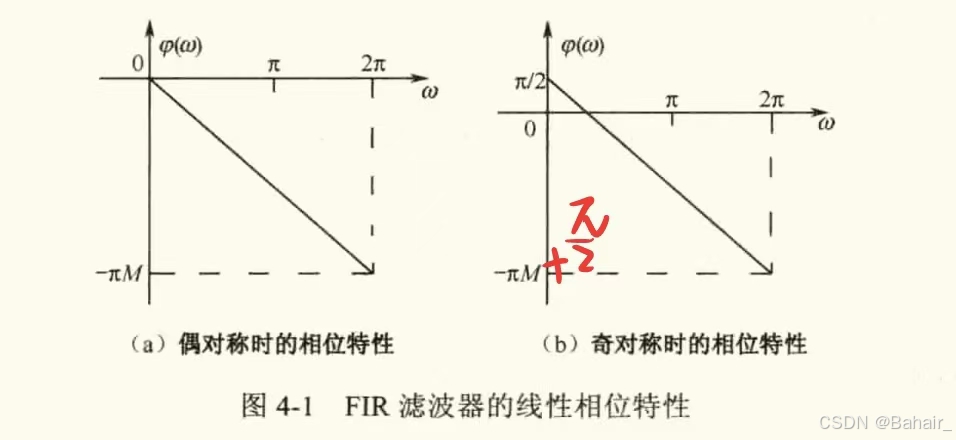
相比于IIR滤波器（无线性相位特征），在相同的性能指标下，所需要的阶数更多，实现时消耗的硬件资源也越多
FIR只在原点处存在极点，FIR滤波器总是稳定且因果的
FIR滤波器不存在反馈结构，因此在FPGA设计中无需考虑因字长无限增长而需要采取的数据截断，只需要知道计算过程中的最大字长即可

单位取样响应特征	相位特性	幅度特性	可设计滤波器种类
偶对称，偶整数	线性相位	w=0、Π、2Π偶对称	各种滤波器
偶对称，奇整数	线性相位	w=Π奇对称，w=0、2Π偶对称	低通、带通
奇对称，偶整数	线性相位，附加90°相移	w=0、Π、2Π奇对称	带通
奇对称，奇整数	线性相位，附加90°相移	w=0、2Π奇对称，w=Π偶对称	高通、带通

注：MATLAB直接设计出的FIR滤波器的系数都是偶对称的。当阶数不满足可设计滤波器的奇偶特征时，MATLAB会自动对阶数进行调整

结构图

具有线性特征时（即滤波器系数为偶对称，可以先求和，再相乘，减少乘法运算）

结构图

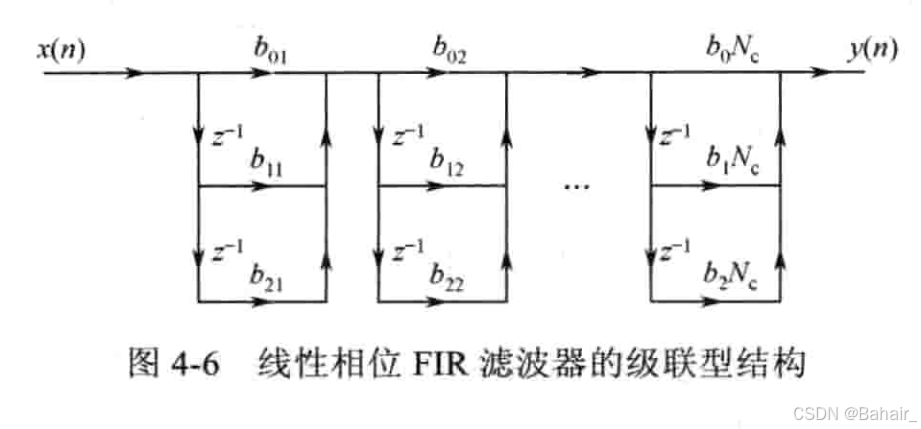
级联型需要的乘法单元比直接型多，因此FPGA实现一般不采用此结构

结构图

结构图（使用循环卷积实现线性卷积）

原理：在时域中进行，通过窗函数截取具有群延时特性为(N-1)/2的理想低通滤波器，截取范围为0~N-1，获得一个因果的N阶FIR滤波器

加窗对理想低通滤波器的影响：

窗函数选择原则：

b = fir1(n, wn)

b = fir1(n, wn, ftype)

b = fir1(n, wn, ftype, window)

b : FIR滤波器的系数，长度为N + 1
n : FIR滤波器的阶数
wn ：截止频率，范围是0~1，其中1为采样频率的一半
- 如果 Wn 是标量，则 fir1 设计的是截止频率为 Wn 的低通或高通滤波器。截止频率是滤波器的归一化增益为 -6 dB 处的频率
- 如果 Wn 是二元素向量 [w1 w2]，其中 w1 < w2，则 fir1 设计的是截止频率下限为 w1 且截止频率上限为 w2 的带通或带阻滤波器
- 如果 Wn 是多元素向量 [w1 w2 ... wn]，其中 w1 < w2 <…< wn，则 fir1 返回一个 n 阶多频带滤波器，频带为 0 < ω < w1、w1 < ω < w2、…、wn < ω < 1
ftype ：指定滤波器类型
- 如果 Wn 是标量，ftype为'high'或'low'
- 如果 Wn 是二元素向量 [w1 w2]，ftype为'bandpass'或'stop'
- 如果 Wn 是多元素向量 [w1 w2 ... wn]，ftype为'DC-0'（Wn 是多元素向量时的默认值）表示第一个频带为阻带，'DC-1'表示第一个频带为通带
window ：指定窗函数类型，如果不指定，默认使用hamming窗