Largest Plus Sign 最大的加号

在从（0,0）到（N-1，N-1）的2D网格中，每个单元格包含1，除了给定列表mines中的那些单元格是0。求在网络中最大的轴对齐加号是什么？ 返回加号的大小。 如果没有，则返回0。
“轴k对齐1的轴对齐加号”具有一些中心网格[x] [y] = 1以及4个长度为k-1的臂向上，向下，向左和向右，并且由1s组成。 这在下面的图表中说明。 请注意，加号的臂外可能有0或1，只检查加号的相关区域1秒。

Examples of Axis-Aligned Plus Signs of Order k:

Order 1:
000
010
000

Order 2:
00000
00100
01110
00100
00000

Order 3:
0000000
0001000
0001000
0111110
0001000
0001000
0000000

Example 1:

Input: N = 5, mines = [[4, 2]]
Output: 2
Explanation:
11111
11111
11111
11111
11011
In the above grid, the largest plus sign can only be order 2.  One of them is marked in bold.

Example 2:

Input: N = 2, mines = []
Output: 1
Explanation:
There is no plus sign of order 2, but there is of order 1.

Example 3:

Input: N = 1, mines = [[0, 0]]
Output: 0
Explanation:
There is no plus sign, so return 0.

Note:

1. N will be an integer in the range [1, 500].
2. mines will have length at most 5000.
3. mines[i] will be length 2 and consist of integers in the range [0, N-1].
4. (Additionally, programs submitted in C, C++, or C# will be judged with a slightly smaller time limit.)

思路：这道题是求以1为中心拓展的最大的十字，我们应该取十字中最短的边作为节点（i，j）的边，最后返回所有节点中最长的节点的十字的边。最笨的办法就是对N*N的每一个节点都遍历它的四个维度（上下左右）的边，这样的复杂度是O(N^3)，我们想想能不能把复杂度降为O(N^2)，具体思路如下图例子所示。

原数组如图所示：

1  0  1  0
1  1  1  1
1  0  1  1

我们需要维护4个二维数组分别表示上下左右的1的信息，即点（i，j）包含自身的四个方向的1的个数

left连续1的次数

1  0  1  0
1  2  3  4
1  0  1  2

right连续1的次数

1  0  1  0
4  3  2  1
1  0  2  1

up连续1的次数

1  0  1  0
2  1  2  1
3  0  3  2

down连续1的次数

3  0  3  0
2  1  2  2
1  0  1  1

那么我们选取4个二维数组对应点（i，j）的最小值最为点（i，j）的十字架的边，最后选取最大的点即可。

我们发现对于每一个确定的点（i，j），一定是up，left，right，dowm中最小的一个。那么我们能不能不用四个二维数组，只用一个二维数组来搞定呢？答案是可以的，我们来看如下代码：

vector<vector<int>> dp(N, vector<int>(N, N));    //初始化dp为N*N的，且默认值为N

对于每个点的更新，核心代码如下：

for (int i = 0; i < N; i++) {
        int l=0,r=0,u=0,d=0;
		for (int j = 0; j < N; j++) {
			dp[i][j] = min(dp[i][j], l=dp[i][j] ? l + 1 : 0);
		}
		for (int j = N-1; j >=0; j--) {
			dp[i][j] = min(dp[i][j], r=dp[i][j] ? r + 1 : 0);
		}
		for (int j = 0; j <N; j++) {
			dp[j][i] = min(dp[j][i], u=dp[j][i] ? u + 1 : 0);
		}
		for (int j = N-1; j >=0; j--) {
			dp[j][i] = min(dp[j][i], d=dp[j][i] ? d + 1 : 0);
		}
	}

其中l，r，u，d分别表示对于（i，j）点而言，左右上下的四条边的对应长度。我们来思考一下为什么只需要一个二维数组就可以完成四个数组的更新，原则是只要对于每个点（i，j），它一定是由左右上下四条边对应的值取最小得到的，那么就一定是正确的。我们通过图例的方式来看一下这段代码是如何更新点的：

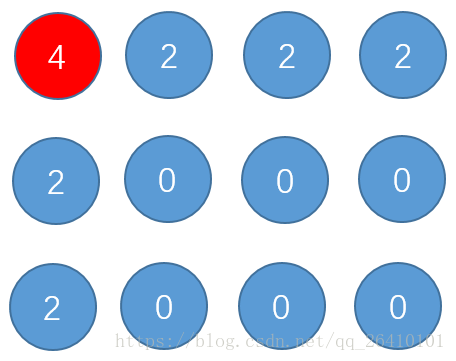
当i=0时：

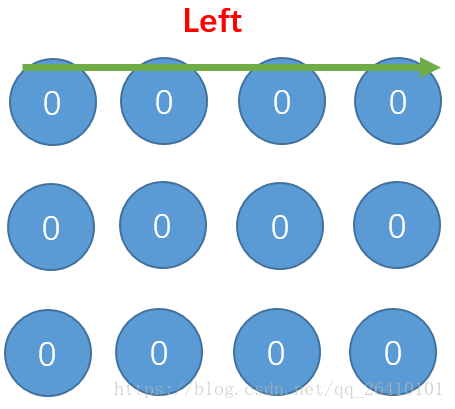
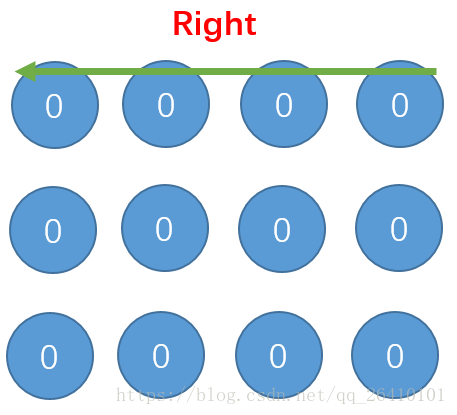
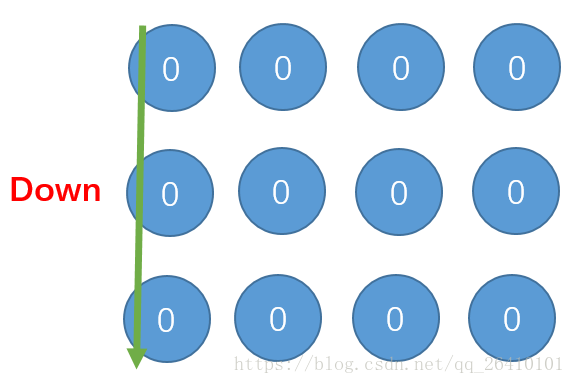
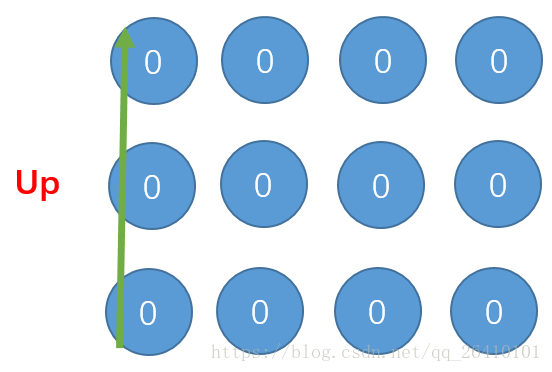
更新完我们发现只有（0,0）点经过了4次更新，即此时只有（0,0）点是正确的:

我们在来看i=1时：

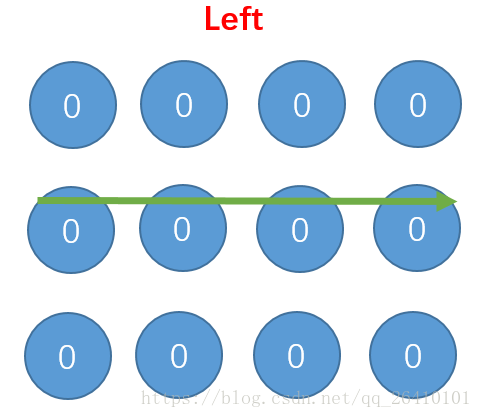
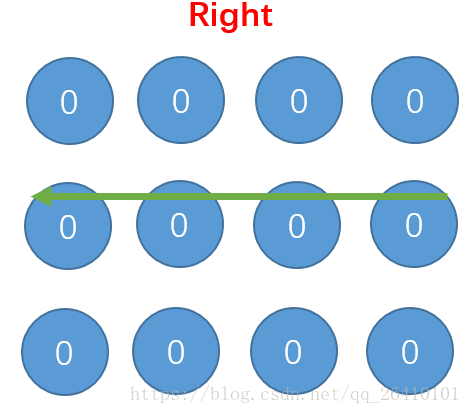
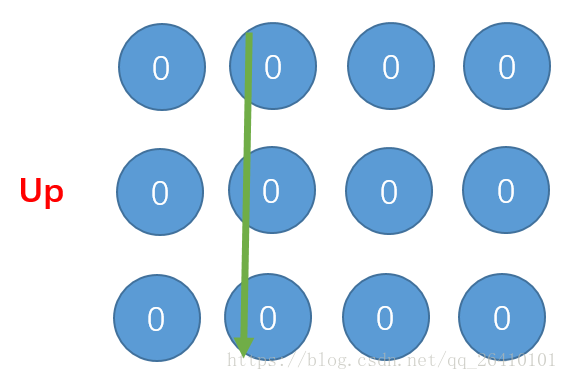
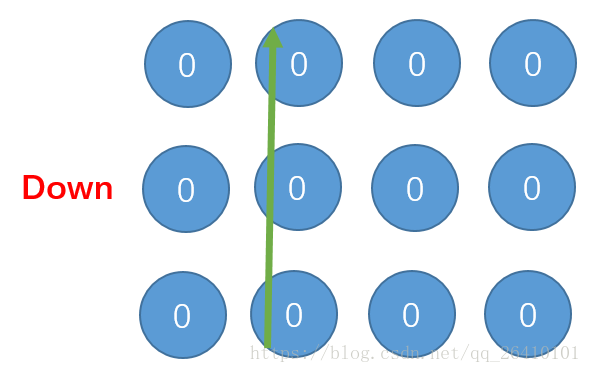
经过i=1的更新，目前有如下几个点经过了4次更新:

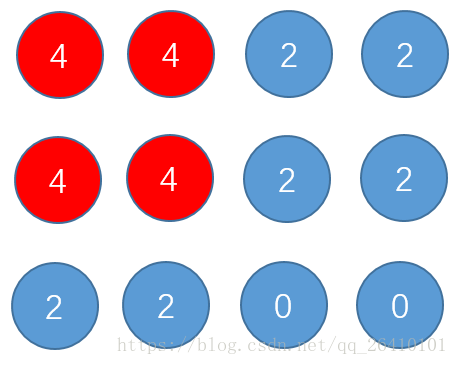
可以看出规律每次像包络一样向外扩散，所以当i=N-1时，最右下角的点也会被更新，满足4次更新，这时我们取二维数组中最大的值即可。

参考代码：

class Solution {
public:
    int orderOfLargestPlusSign(int N, vector<vector<int>>& mines) {
	int res = 0;
	vector<vector<int>> dp(N, vector<int>(N, N));
	for (int i = 0; i < mines.size(); i++) {
		dp[mines[i][0]][mines[i][1]] = 0;
	}
	for (int i = 0; i < N; i++) {
        int l=0,r=0,u=0,d=0;
		for (int j = 0; j < N; j++) {
			dp[i][j] = min(dp[i][j], l=dp[i][j] ? l + 1 : 0);
		}
		for (int j = N-1; j >=0; j--) {
			dp[i][j] = min(dp[i][j], r=dp[i][j] ? r + 1 : 0);
		}
		for (int j = 0; j <N; j++) {
			dp[j][i] = min(dp[j][i], u=dp[j][i] ? u + 1 : 0);
		}
		for (int j = N-1; j >=0; j--) {
			dp[j][i] = min(dp[j][i], d=dp[j][i] ? d + 1 : 0);
		}
	}
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			res = max(res, dp[i][j]);
		}
	}
	return res;        
    }
};