鲁棒优化（二）

目录

一、参数的不确定集

1.1  盒式不确定集（Box Uncertainty Set）

1.2  椭球不确定集（Ellipsoidal Uncertainty Set）

1.3 基数/预算不确定集（Budget uncertainty Set）

1.4 多面体不确定集（Polyhedral Uncertainty Set）

1.5 数据驱动的不确定集（Data-driven Uncertainty Set）

1.6 其他组合的不确定集合

二、对等式转换理论（Robust counterpart）

2.1 Soyster的鲁棒对等模型（矩阵A的参数不确定）

2.2 Ben-tal和Nemirovski鲁棒对等模型

2.3 Bertsimas和Sim鲁棒对等模型

一、参数的不确定集

在鲁棒优化（一）中，我们知道鲁棒优化的求解困难点在于不确定集合的确立，由于不同的不确定集对结果影响十分明显，如果不确定集越精细，模型复杂度就将会越高，求解也就会变的愈加的困难。而当不确定集越宽泛时，所求出的最优解越保守，越是不符合实际的。

因此，基于上述分分析，为了权衡精细和宽泛的关系也为了平衡求解难度和求解精度，如何选择一个适合的不确定集来求解鲁棒优化就显然更为重要了。常见的不确定集主要有如下几类:

1.1  盒式不确定集（Box Uncertainty Set）

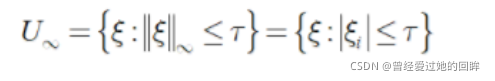
 盒式不确定集是最简单的不确定集类型，也被称之为区间集，试想一下所有参数都有一个上下界，那么不就类似于一个盒子嘛。由于鲁棒优化是考虑