剑指Offer刷题笔记——数组中的逆序对

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007。

首先是暴力的方法，算法复杂度是O(n*2)。

分治思想，采用归并排序的思路来处理：

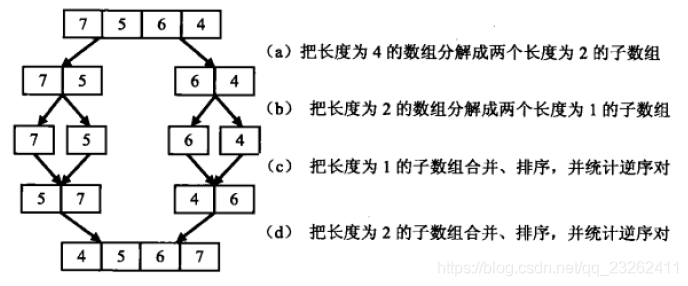
先把数组分解成两个长度为2的子数组，再把这两个子数组分解成两个长度为1的子数组。接下来一边合并相邻的子数组，一边统计逆序对的数目。在第一对长度为1的子数组{7}、{5}中7>5，因此（7,5）组成一个逆序对。同样在第二对长度为1的子数组{6}，{4}中也有逆序对（6,4），由于已经统计了这两对子数组内部的逆序对，因此需要把这两对子数组进行排序，避免在之后的统计过程中重复统计。

逆序对的总数 = 左边数组中的逆序对的数量 + 右边数组中逆序对的数量 + 左右结合成新的顺序数组时中出现的逆序对的数量。

考虑合并两个有序序列时，计算逆序对数。
对于两个升序序列，设置两个下标：两个有序序列的末尾。每次比较两个末尾值，如果前末尾大于后末尾值，(说明前面的末尾大于后面的所有值)。则有”后序列当前长度“个逆序对；否则不构成逆序对。然后把较大值拷贝到辅助数组的末尾，即最终要将两个有序序列合并到辅助数组并有序。

其实这题就是利用的就是普通的归并排序，只不过是在交换两个数字顺序的时候，要计数。

# -*- coding:utf-8 -*-
class Solution:
    def InversePairs(self, data):
        # write code here
        if not data:
            return 0
        # 这块如果temp = data,temp和data是一个变量
        # 用列表的解析方式,temp和data是两个相同的变量。
        temp = [i for i in data]
        return self.mergeSort(temp, data, 0, len(data)-1) % 1000000007
       
    def mergeSort(self, temp, data, low, high):
        # 只有分到最小区间才返回
        if low >= high:
            temp[low] = data[low]
            return 0
        mid = (low + high) / 2
        # data和temp传参数是位置变换了，一个列表被切分，另一个列表存储排序之后的结果。
        # 两个列表交替功能。
        left = self.mergeSort(data, temp, low, mid)
        right = self.mergeSort(data, temp, mid+1, high)
           
        count = 0
        i = low
        j = mid+1
        index = low
        # 找逆序数
        while i <= mid and j <= high:
            if data[i] <= data[j]:
                temp[index] = data[i]
                i += 1
            else:
                temp[index] = data[j]
                count += mid-i+1
                j += 1
            index += 1
        # 把前面的列表剩下的放过去
        while i <= mid:
            temp[index] = data[i]
            i += 1
            index += 1
        # 把后面的列表剩下的放过去
        while j <= high:
            temp[index] = data[j]
            j += 1
            index += 1
        return count + left + right