Lect3 最优化Optimization

Reference

• https://zhuanlan.zhihu.com/p/21387326?refer=intelligentunit
• https://zhuanlan.zhihu.com/p/21360434?refer=intelligentunit

简介

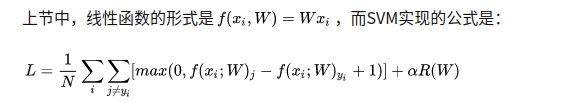
最优化是求一个最佳的$W$使得$L$最小，$L$由score function 和 loss function组成。

损失函数可视化

在两个维度上的loss值切片图，red表示large loss，blue表示small loss

最优化

• 策略#1：随机搜索

W = np.random.randn(10, 3073) * 0.0001 # generate random parameters

• 策略#2：随机局部搜索

step_size = 0.0001
  Wtry = W + np.random.randn(10, 3073) * step_size

• 策略#3：跟随梯度
  当函数有多个参数的时候，我们称导数为偏导数。而梯度就是在每个维度上偏导数所形成的向量。
  

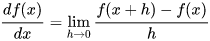
梯度计算

使用有限差值进行数值计算

def eval_numerical_gradient(f, x):
  """  
  一个f在x处的数值梯度法的简单实现
  - f是只有一个参数的函数
  - x是计算梯度的点
  """ 

  fx = f(x) # 在原点计算函数值
  grad = np.zeros(x.shape)
  h = 0.00001

  # 对x中所有的索引进行迭代
  it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
  while not it.finished:

    # 计算x+h处的函数值
    ix = it.multi_index
    old_value = x[ix]
    x[ix] = old_value + h # 增加h
    fxh = f(x) # 计算f(x + h)
    x[ix] = old_value # 存到前一个值中 (非常重要)

    # 计算偏导数
    grad[ix] = (fxh - fx) / h # 坡度
    it.iternext() # 到下个维度

  return grad

实际中用中心差值公式（centered difference formula）效果更好。

微分计算梯度

梯度告诉我们损失函数在每个维度上的斜率，以此来进行更新。

• 步长的影响（learning rate）：梯度指明了函数在哪个方向是变化率最大的，但是没有指明在这个方向上应该走多远。步长的影响，
  
• 在梯度负方向上更新

梯度下降

# 普通的梯度下降

while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # 进行梯度更新

• 小批量数据梯度下降（Mini-batch gradient descent）
  在大规模的应用中（比如ILSVRC挑战赛），训练数据可以达到百万级量级。如果像这样计算整个训练集，来获得仅仅一个参数的更新就太浪费了。一个常用的方法是计算训练集中的小批量（batches）数据。例如，在目前最高水平的卷积神经网络中，一个典型的小批量包含256个例子，而整个训练集是多少呢？一百二十万个。这个小批量数据就用来实现一个参数更新：

# 普通的小批量数据梯度下降

while True:
  data_batch = sample_training_data(data, 256) # 256个数据
  weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
  weights += - step_size * weights_grad # 参数更新

**这个方法之所以效果不错，是因为训练集中的数据都是相关的。**小批量数据的大小是一个超参数，但是一般并不需要通过交叉验证来调参。它一般由存储器的限制来决定的，或者干脆设置为同样大小，比如32，64，128等。之所以使用2的指数，是因为在实际中许多向量化操作实现的时候，如果输入数据量是2的倍数，那么运算更快。