KMP算法（无回溯字符串匹配）基于python实现

1.问题导出

给你两个字符串，一个是目标串，比如是“ababcabccacbab”，另一个是模式串，比如是“abcac”，现在想在目标串中找出是否含有模式串的子串，如果有，返回第一个字母的下标，如果无，返回-1

当运用朴素的串匹配算法去解答该题时，分为以下两步：

（1）目标串与模式串从左到右依次匹配

（2）当发现不匹配时，转去考虑考虑目标串里的下一个位置是否与模式串匹配

思路非常简单，但是当考虑复杂度时，可以发现，在在坏的情况下，比如：

目标串：“aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaab”

模式串：“aaaab”

在这里，时间复杂度达到了O（n*m），n为目标串长度，m为模式串长度。在朴素的匹配算法下，由于认为字符串前后是完全独立，所以每次匹配时，都是从头开始匹配，所以效率很低。但是，大部分的字符串都是相关联的。例如在上述的模式串“abcac”中，

 

按照朴素串匹配算法，当左图中的最后一个字符不匹配时，下一步，是目标串重新开始用另一个字符与模式串做匹配。但是完全可以如下图所示直接跳到更远的地方，拿开始的a与目标串中的a直接做匹配。

这便是KMP算法的由来。

2. KMP算法

先考虑朴素的串匹配算法和KMP匹配的过程：

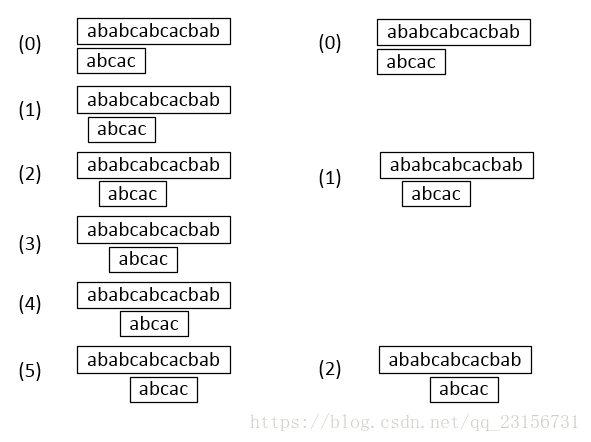
上图左边是朴素串匹配算法的一系列情况。状态0的匹配进行到模式串中字符c时失败，此前有两次成功匹配，从