深度学习之损失(Loss)函数的介绍【详解】

本文链接：https://blog.youkuaiyun.com/qq_23022733/article/details/125537249

本文详细介绍了常用的深度学习损失函数，包括CrossEntropyLoss、BinaryCrossEntropyLoss、FocalLoss、smoothL1Loss以及针对目标检测优化的IOU、GIOU、CIOU损失。重点阐述了这些损失函数的数学公式、应用场景及优缺点，特别是针对正负样本不平衡和定位精度提升的解决方案。通过实例代码对比了自定义的smoothL1Loss与PyTorch内置实现的差异。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

1、Cross Entropy Loss（交叉熵）

公式：
$L=-\sum _i y_i \cdot log(p_i)$

其中 $y_i$ 为人工标注的， $p_i$ 为预测的概率；

参考：链接1，链接2，这个链接解释的最清晰链接3

2、Binary Cross Entropy Loss（二元交叉熵）

公式：
$H_{p(q)}=-\frac{1}{N}[\sum^N_{i=1}y_i \cdot log(p(y_i))+(1-y_i) \cdot log(1-p(y_i))]$
$[]$ 里面表示的是单个样本分别预测正样本和负样本的概率。

3、Balance Binary Cross Entropy Loss（平衡二元交叉熵）

在这里插入图片描述
目的：解决正负样本不平衡的问题。

4、Focal Loss

在这里插入图片描述
$(1-p)^\gamma$ 用于难样本的挖掘，如一个样本预测正样本的概率较低，则 $(1-p)^\gamma$ 会加大正样本的权重， $p^\gamma$ 会减少负样本的权重；

5、smoothL1 Loss

smoothL1 Loss手写代码与torch封装的smoothL1 Loss比较：

import torch
import torch.nn.functional as F
# 自己设计的smooth_l1_loss
def smooth_l1_loss(a, b):
    loss_part1 = torch.abs(a - b)
    loss_part2 = loss_part1 ** 2
    loss_part2 = loss_part2 * 0.50
    loss2 = torch.where(loss_part1 >= 1, loss_part1 - 0.5, loss_part2)
    #下面是统计每个预测框的loss
    #loss2 = torch.sum(loss2, dim = 1) 
    #最终返回的是所有预测框的loss
    loss2 = torch.sum(loss2)
    return loss2

def test_smmoth_l1_loss():
    loc_p = torch.tensor([1, 5, 3, 0.5])
    loc_t = torch.tensor([4, 1, 0, 0.4])
    loss_1 = F.smooth_l1_loss(loc_p, loc_t, size_average=False)
    print ("F.smooth_l1_loss:", loss_1)
    loss_2 = smooth_l1_loss(loc_p, loc_t)
    print ("smooth_l1_loss:", loss_2)

参考：链接1，链接2

6、IOU，GIOU，CIOU

6.1 IOU损失

如下图，绿色框是ground truth，蓝色框是预测框，则，
$IOU=\frac{绿色框面积\cap蓝色框面积}{绿色框面积\cup蓝色框面积}$
IOU损失一般用 $l oss = 1 - I O U$ 即可

IOU损失存在的问题：

没有相交则IOU=0无法梯度计算，
相同的IOU却反映不出实际情况到底咋样

在这里插入图片描述

6.2 GIOU损失

为了解决IOU损失产生的问题，引入了GIOU
GIOU的计算公式：
$L_{GIoU}=1-IoU+\frac{\mid C-B\cup B^{gt}\mid}{\mid C\mid}$

引入了最小封闭形状C (C可以把A，B包含在内)，在不重叠情况下能让预测框尽可能朝着真实框前进

在这里插入图片描述

GIOU存在的问题，如果预测框和真实框重叠，也会出现IoU一样，但预测框与真实框的分布不一样，

在这里插入图片描述

6.3 DIoU损失

DIoU公式：
$L_{DIoU}=1-IoU+\frac{\rho^2(b,b^{gt})}{c^2}$

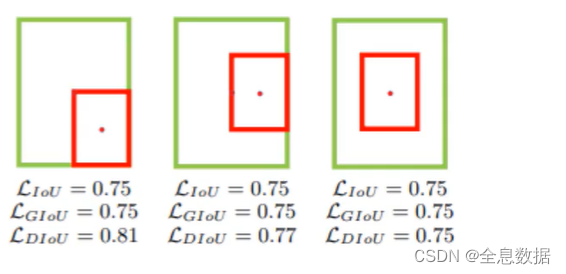
其中分子计算预测框与真实框的中心点欧式距离 d，分母是能覆盖预测框与真实框的最小BOX的对角线长度 c，直接优化距离，速度更快,并解决GIOU问题，如下图所示，

在这里插入图片描述

6.4 CIOU损失

CIOU公式：
$L_{CIoU}=1-IoU+\frac{\rho^2(b,b^{gt})}{c^2}+\alpha \nu$
$\alpha=\frac{\nu}{(1-IoU)+\nu}$
$\nu=\frac{4}{\pi^2}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h})^2$