CUDA学习笔记（LU分解）

最新推荐文章于 2025-06-15 23:22:42 发布

原创

最新推荐文章于 2025-06-15 23:22:42 发布 · 6.5k 阅读

37 ·

CC 4.0 BY-SA版权

文章标签：

#笔记

本文介绍了CUDA环境下实现LU分解的过程，包括基本的LU算法、并行化策略，特别是right-looking算法的CUDA实现。文章讨论了CUDA编程中遇到的问题，如线程同步、累计操作和矩阵大小对性能的影响，并给出了64*64矩阵的运行时间。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

最近在学习LU的并行加速，从paper中得到了一些idea，就想着用GPU来实现一下。学习CUDA的过程中踩了不少坑，不过最终还是完成了测试。

一、LU基本算法

1、LU 分解是计算机做矩阵运算过程中重要的一步，通过将矩阵分解为一个上三角矩阵U和下三角矩阵L，能够有效的缩短计算时间。

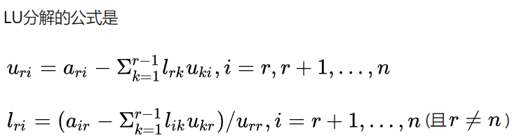
LU分解的计算过程如下，采用高斯消元法。
源自知乎

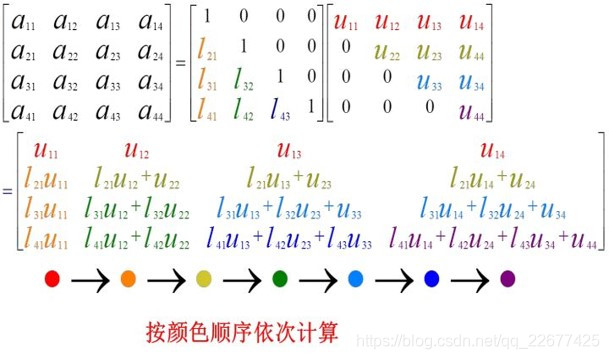
2、基本算法

每一次循环都将A的第i行和第i列更新为L\U的一部分。
每一次循环分为三个部分。如果先计算左上角的元素，则下侧的L矩阵部分和右侧的U矩阵部分可以同时运算，没有干扰。比如当i==1时，因为更新L的第一列（l32、l42）需要先得到u22的值，而u22要通过更新U的第二行得到，所以如果先计算出u22，L和U的更新就可以并行了。

void lud_base(int *a, int size)
{
     int i,j,k;
     int sum;
     for (i=0; i<size; i++)
     {
        //先计算左上角的U元素
        sum=a[i*size+i];
        for (k=0; k<i; k++) sum -= a[i*size+k]*a[k*size+i];
        a[i*size+i]=sum;
        //计算下侧的L矩阵部分
        for (j=i+1;j<size; j++)
        {
             sum=a[j*size+i];
             for (k=0; k<i; k++) sum -=a[j*size+k]*a[k*size+i];
             a[j*size+i]=sum/a[i*size+i];
        }
        //计算右侧的U矩阵部分
        for (j=i+1; j<size; j++)
        {
             sum=a[i*size+j];
             for (k=0; k<i; k++) sum -=