网络流最大流+拆点+路径输出

最新推荐文章于 2020-07-31 20:55:39 发布

原创最新推荐文章于 2020-07-31 20:55:39 发布 · 882 阅读

0 ·

CC 4.0 BY-SA版权

网络流专栏收录该内容

9 篇文章

订阅专栏

本文通过网络流模型解决了一个关于电脑公司如何最大化单位时间产量的问题。具体地，通过建立一个包括原点S、汇点T和各个机器节点的网络，利用Dinic算法求解最大流，并进一步确定了哪些机器之间存在协作关系。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：http://poj.org/problem?id=3436
题目大意：
电脑公司生产电脑有N个机器，每个机器单位时间产量为Qi。电脑由P个部件组成，每个机器工作时只能把有某些部件的半成品电脑(或什么都没有的空电脑）变成有另一些部件的半成品电脑或完整电脑(也可能移除某些部件）。求电脑公司的单位时间最大产量，以及哪些机器有协作关系，即一台机器把它的产品交给哪些机器加工。

Sample input

3 4

15 0 0 0 0 1 0

10 0 0 0 0 1 1

30 0 1 2 1 1 1
3 0 2 1 1 1 1

Sample output

25 2

1 3 15

2 3 10

输入：电脑由3个部件组成，共有4台机器，1号机器产量15, 能给空电脑加上2号部件，2号机器能给空电脑加上2号部件和3号部件, 3号机器能把有1个2号部件和3号部件有无均可的电脑变成成品（每种部件各有一个）
输出：单位时间最大产量25,有两台机器有协作关系，
1号机器单位时间内要将15个电脑给3号机器加工
2号机器单位时间内要将10个电脑给3号机器加工

思路：

网络流模型：

添加一个原点S,S提供最初的原料 00000…
添加一个汇点T, T接受最终的产品 11111…
将每个机器拆成两个点: 编号为i的接收节点，和编号为i+n的产出节点（n是机器数目），前者用于接收原料，后者用于提供加工后的半成品或成品。这两个点之间要连一条边，容量为单位时间产量Qi
S 连边到所有接收 “0000…” 或 “若干个0及若干个2” 的机器，容量为无穷大
产出节点连边到能接受其产品的接收节点，容量无穷大
能产出成品的节点，连边到T，容量无穷大。
求S到T的最大流

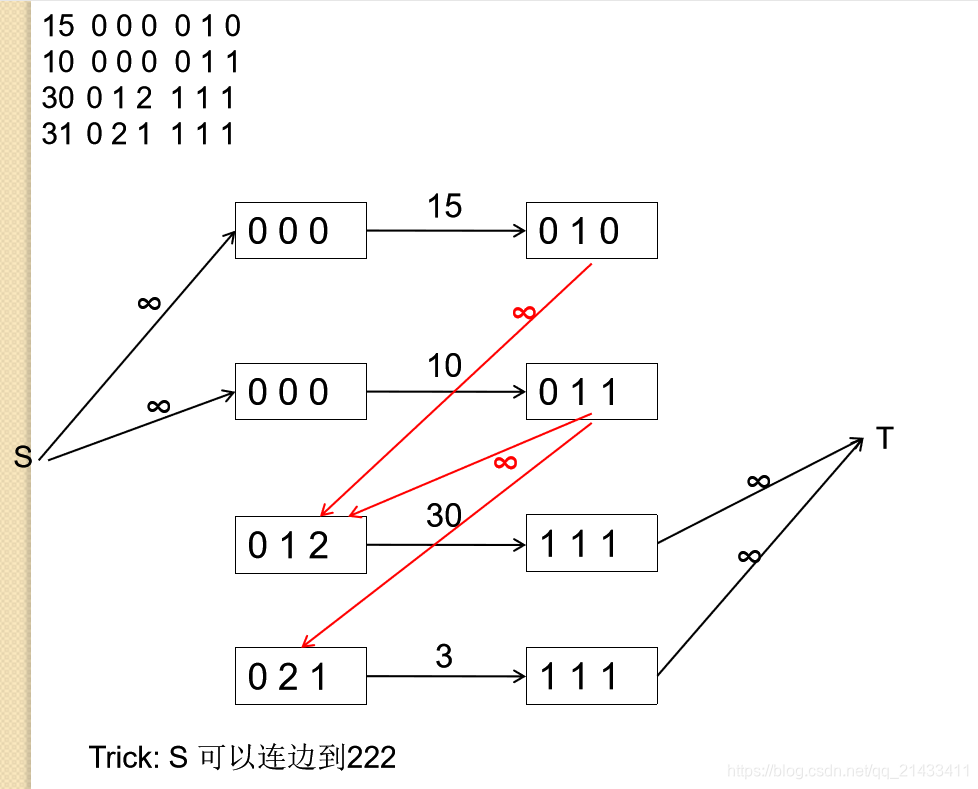
坑点：s可以与只包含0和2的连接。

路径输出：残流网络反向边。

#include<bits/stdc++.h>
using namespace std;

int s[2][55][15];
int L[55];

const int maxn=1e5+10;
const int maxm=2e5+10;

struct E
{
    int v;   //每一条边指向的点
    int next;//指向对应点的前一条边
    int w;   //每一条边的残量

}e[maxm];

int ss, tt;//源点和汇点
int cut;//边的数量，从0开始编号
int head[maxm];//每一个点最后一条边的编号
int d[maxn];//分层图中标记深度
int inf=(1<<31)-1;
int cur[maxn];//cur就是记录当前点u循环到了哪一条边
int n, m;

void init()
{
    cut=-1;
    memset(head, -1, sizeof(head));
}

void addEdge(int u, int v, int w)
{
    cut++;
    e[cut].next=head[u];
    e[cut].v=v;
    e[cut].w=w;
    head[u]=cut;
}

void add(int u, int v, int w)
{
    addEdge(u, v, w);
    addEdge(v, u, 0);
}

int bfs()
{
    queue<int> q;
    while(!q.empty())
    {
        q.pop();
    }
    memset(d, 0, sizeof(d));
    d[ss]=1;
    q.push(ss);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i!=-1;i=e[i].next)
        {
            int v=e[i].v, w=e[i].w;
            if(w>0&&d[v]==0)
            {
                d[v]=d[u]+1;
                q.push(v);
            }
        }
    }
    if(d[tt]==0)
    {
        return 0;
    }

    return 1;
}

int dfs(int u, int dis)
{
    if(u==tt)
    {
        return dis;
    }

    for(int &i=cur[u];i!=-1;i=e[i].next)
    {
        int v=e[i].v, w=e[i].w;
        if((d[v]==d[u]+1)&&w!=0)
        {
            int di=dfs(v, min(dis, w));
            if(di>0)
            {
                e[i].w-=di;
                e[i^1].w+=di;
                return di;
            }
        }
    }

    return 0;
}

int Dinic()
{
    int ans=0;
    while (bfs())
    {
        for(int i=ss;i<=tt;i++)
        {
            cur[i]=head[i];
        }
        while (int d=dfs(ss,inf))
        {
            ans+=d;
        }
    }
    return ans;
}

int main()
{
    int p, n;
    while(scanf("%d%d",&p,&n)!=EOF)
    {
        init();
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&L[i]);
            for(int j=0;j<p;j++)
            {
                scanf("%d",&s[0][i][j]);
            }
            for(int j=0;j<p;j++)
            {
                scanf("%d",&s[1][i][j]);
            }
        }
        for(int i=1;i<=n;i++)
        {
            add(i, i+n, L[i]);
            for(int j=1;j<=n;j++)
            {
                if(i==j)
                {
                    continue;
                }
                else
                {
                    int q=0;
                    for(int k=0;k<p;k++)
                    {
                        if(s[0][j][k]!=2)
                        {
                            if(s[1][i][k]!=s[0][j][k])
                            {
                                q=1;
                                break;
                            }
                        }
                    }
                    if(q==0)
                    {
                        add(i+n, j, inf);
                    }
                }
            }
        }
        for(int i=1;i<=n;i++)
        {
            int q=0;
            for(int j=0;j<p;j++)
            {
                if(s[0][i][j]==1)
                {
                    q=1;
                    break;
                }
            }
            if(q==0)
            {
                add(0, i, inf);
            }
            q=0;
            for(int j=0;j<p;j++)
            {
                if(s[1][i][j]!=1)
                {
                    q=1;
                    break;
                }
            }
            if(q==0)
            {
                add(i+n, 2*n+1, inf);
            }
        }
        ss=0, tt=2*n+1;
        cout<<Dinic()<<" ";

        int ans=0;
        for(int i=1;i<=n;i++)
        {
            for(int j=head[i];j!=-1;j=e[j].next)
            {
                if(e[j].w!=0&&e[j].v!=0&&e[j].v!=i+n)
                {
                    ans++;
                }
            }
        }
        cout<<ans<<endl;
        for(int i=1;i<=n;i++)
        {
            for(int j=head[i];j!=-1;j=e[j].next)
            {
                if(e[j].w!=0&&e[j].v!=0&&e[j].v!=i+n)
                {
                    printf("%d %d %d\n",e[j].v-n,i, e[j].w);
                }
            }
        }
    }

    return 0;
}

/*
1 3
10 0 1
10 2 1
20 1 0
*/