【论文阅读笔记】Performance Guaranteed Network Accelerationvia High-Order Residual Quantization

方法概括

  该方法在总结前人的基础上（BNN,Binarized Neural Network；Xnor-Net），提出了一个High-Order（高阶）的二元逼近方法。高阶的定义在于，原始的逼近会存在量化残差(Residual Quantization)，而用另一个矩阵去逼近“遗失”的参数，这是一个迭代的过程，也就是越来越高阶的过程。最后得到的逼近矩阵，是原始逼近 + 迭代“遗失”逼近。
  经过速度和精度的综合思考，作者选择 将 W 进行一阶量化（BWH已经证明权重的二值化可以在大型数据集 ImageNet达到state-of-art的结果），而将 layer input 进行二阶量化。

注意，作者说是为了解决XNOR-Net的量化问题（展示的结果，只是在简单网络上的量化比XNOR-Net好一点），但其检验结果只展示了在 Mnist 和 CIFAR-10 两个数据集上，可能在大数据集上(ImageNet)的结果不太好。

---

Introduction

  Network Pruning不能提供一个统一的方法去让网络推测加速和压缩，其需要“专业知识”去完成。Network Binarization也是一个网络加速和压缩的方法(BinaryConect-Network可以在小型数据集，如CIFAR-10和SVHN达到好结果；Binary-Weights-Network, BWN在大型网络ImageNet数据集达到state-of-art结果，且达到了约32倍的模型压缩)。
  考虑到，若weight 和 layer input都为二值化，则乘法操作会变成异或操作，这能进一步的加速。但先前的网络二值化方法，如BNN和XNOR-NET，在极大加速的同时（58倍加速），也剧烈地降低了准确率(在ImageNet上分别从56.6%掉到27.9%和44.2%)。
  所以，作者想到了递归地通过近似权重逼近留下的残差，来增加二元逼近的效果。

---

Related Work

  不同于 Parameter Pruning的方法，作者的High-Order Residual Quantization【HORQ】方法并不依赖于已经预训练好的网络。
  对于网络二值化的方法，BWN(Binary-Weights-Networks，对weight进行二值化)和 XNOR-Networks(对 weight 和 layer input进行二值化) 比 BC (BinaryConnect) 和 BN (BinaryNet)更好的一点在于，其有一个重要的创新点：引入了尺度因子 (scaling factor). XNOR-Networks 进一步加速了网络推测过程，但其精确度也损失严重(因为对 layer input也进行了量化，其带来了信息损失)。
  作者提出的HORQ方法的目的就是减少这个量化损失。

---

HORQ Network

  HORQ方法利用 Residual进行递归利用，将 layer input 量化成一系列不同尺度的 binary inputs的和。

XNOR-Network Revisited

  假设 $I$ 是 input tensor，$W$ 是 weight filter，$\ast$是卷积过程。
  XNOR-Net 使用 KaTeX parse error: Expected 'EOF', got '\alphaB' at position 1: \̲a̲l̲p̲h̲a̲B̲来逼近 $W$ ，其中 $\alpha \in R^{+}$ 是尺度因子，B∈{−1,+1}c∗w∗hB \in \{ -1, +1\}^{c*w*h}B∈{−1,+1}c∗w∗h，则二元卷积变成了：$$I\ast W\approx \alpha (I\oplus B)$$  其中，$\oplus$代表不用乘法的二元卷积操作。

  而求解 $\alpha$ 和 $B$ 的优化过程如下：$${\alpha }^{\ast }，B^{\ast }=argmi{n}_{\alpha ，B}J(B,\alpha )=argmi{n}_{\alpha ,B}\Vert W-\alpha B{\Vert }^2$$
  该优化问题的解为：$$\{\begin{array}{l}{B}^{\ast }=sign(W)\\ {\alpha }^{\ast }=\frac{1}{n}\Vert W{\Vert }_{l_1}\end{array}$$
  同样的，XNOR使用 $\beta H$ 来逼近 input tensor $X$：$X\approx \beta H$，而它们的优化问题变为：$${\alpha }^{\ast },B^{\ast },{\beta }^{\ast },H^{\ast }=argmi{n}_{\alpha ,B,\beta ,H}\Vert X\odot W-\alpha \beta H\odot B{\Vert }^2$$
  该优化问题的解为：$$\{\begin{array}{l}{\alpha }^{\ast }{B}^{\ast }=\frac{1}{n}\Vert W{\Vert }_{l_1}sign(W)\\ {\beta }^{\ast }{H}^{\ast }=\frac{1}{n}\Vert X{\Vert }_{l_1}sign(H)\end{array}$$

High-Order Residual Quantization

  HORQ方法，在进行卷积之前，需要将 Tensors Reshape 成 Matrices。其逼近是以向量为单位进行的。对于输入向量 $X\in R^n$，我们像XNOR-Net 一样量化$X$：$$X\approx {\beta }_1{H}_1\text{\hspace{1em}(1)}$$  其中β1∈R，H1∈{+1,−1}\beta_1 \in R，H_1 \in \{ +1, -1 \}β1​∈R，H1​∈{+1,−1}。可以得到解为：$$\{\begin{array}{l}{H}_1^{\ast }=sign(X)\\ {\beta }_1^{\ast }=\frac{1}{n}\Vert X{\Vert }_{l_1}\end{array}\text{\hspace{1em}(2)}$$  我们可以将 公式$(1)$作为 一阶二值量化。因此可以得到一阶残差张量(真实输入值和二值逼近值之间的差)$$R_1(X)=X-{\beta }_1{H}_1$$  我们可以像公式$(1)$一样，二值逼近$R_1(X)$，逼近结果为：$$R_1(X)\approx {\beta }_2{H}_2$$  其中，β2∈R，H2∈{+1，−1}n\beta_2 \in R，H_2 \in \{+1，-1\}^nβ2​∈R，H2​∈{+1，−1}n。这个逼近，可以认为是二阶Residual Quantization 。所以，输入$X$可以被认为是如下逼近：$$X={\beta }_1{H}_1+R_1(X)\approx {\beta }_1{H}_1+{\beta }_2{H}_2$$  其中，${\beta }_1，{\beta }_2$是实数值，而$H_1，H_2$是二值$tensors$，${\beta }_1{H}_1$成为一阶二值输入，${\beta }_2{H}_2$是二阶二值输入，二阶二值输入的结果可以同样由公式$(2)$得出。

  事实上，我们可以递归的计算高阶的residual tensor，但是随着阶数的变高，计算也随之变得昂贵。作者发现二阶/三阶的量化结果已经足够好。

The HORQ Network

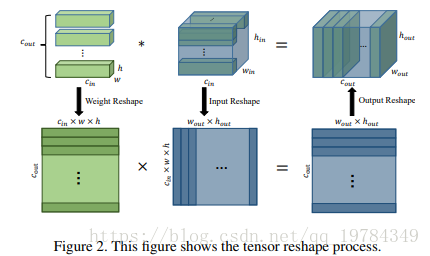
Tensor Reshape

  对于每一个 weight filter $W$而言，其 shape 为 $c_{in}\ast w\ast h$，则可以直接将每个卷积核 reshape 成一个向量 $1\ast (c_{in}\ast w\ast h)$。则对于每层的 weight tensor 而言，可以 reshape 成 $c_{out}\ast (c_{in}\ast w\ast h)$。
  对于卷积层的输出 $Y$而言，其大小为 $<X,W,\ast >$，Y∈{Rcout∗wout∗hout}Y \in \{ \mathcal{R}^{c_{out}*w_{out}*h_{out}} \}Y∈{Rcout​∗wout​∗hout​}，其中$w_{out}=\frac{w_{in}+2\ast p-w}{s}+1$，$h_{out}=\frac{h_{in}+2\ast p-h}{/}s+1$，其中 $p$ 和 $s$ 分别代表 padding 和 stride。
  对于 input tensor $X$，我们可以将每个与卷积核对应大小的 sub-tensor 展开成向量，然后将他们集合成 Matrix $X$。一共有 $w_{out}\ast h_{out}$个 sub-tensor。所以，X的形状为 $(c_{in}\ast w\ast h)\ast (w_{out}\ast h_{out})$

Convolution Using Order-Two Residual Quantization

  对 $W_r$ 的每一行 $W_{r_i}$都进行一阶二值逼近：$$\begin{gathered} W_{r(i)}\approx {\alpha }_i{B}_i(i=1，2，...，c_{out}) \\ \{\begin{array}{l}{B}_i=sign(W_{r(i)})\\ \alpha =\frac{1}{c_{in}\ast w\ast h}\Vert W_{r(i)}{\Vert }_{l_1}\end{array} \end{gathered}$$

  对每一层的 input matrix $X$的每一列进行二阶残差量化：$$X_{r(i)}\approx {\beta }_{1(i)}{H}_{1(i)}+{\beta }_{2(i)}{H}_{2(i)}(i=1，2，...，w_{out}\ast h_{out})$$$$\{\begin{array}{l}{H}_{1(i)}=sign(X_{r(i)})\\ {\beta }_{1(i)}=\frac{1}{c_{in}\ast w\ast h}\Vert X_{r(i)}{\Vert }_{l_1}\\ R_1(X_{r(i)})=X_{r(i)}-{\beta }_{1(i)}{H}_{1(i)}\\ H_{2(i)}=sign(R_1(X_{r(i)}))\\ bet{a}_{2(i)}=\frac{1}{c_{in}\ast w\ast h}\Vert R_1(X_{r(i)}){\Vert }_{l_i}\end{array}$$

Training HORQ

  HORQ的训练方法和平常的量化网络训练方法没什么不同：利用连量化好的权值和输入进行 Forward 和 Backward，在全精度上进行 参数更新。在训练流程上，作者特意说出了学习率 $lr$ 的衰减，但没给公式，不知道有没什么特殊的地方。

---

Experiments

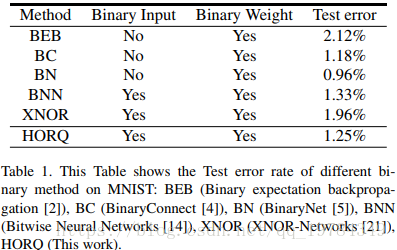
Mnist

  为了和BC、BN比较，这个网络使用了 3层的MLP，使用Adam从头训练。

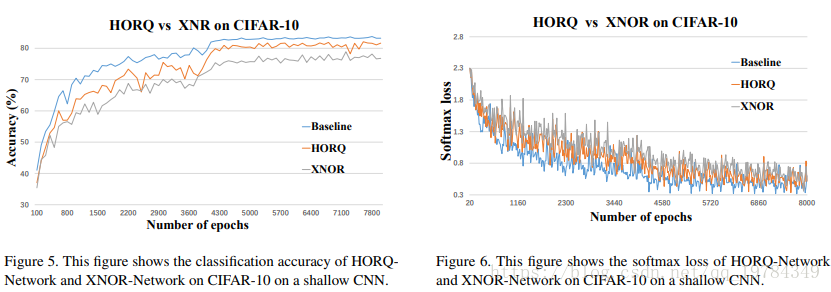
CIFAR-10

  在CIFAR数据集，在一个较为简单的网络（3个卷积层，一个全连接层），比XNOR-Net好3%左右。