有权图

最新推荐文章于 2022-07-07 08:25:31 发布

刘扬俊

最新推荐文章于 2022-07-07 08:25:31 发布

阅读量6.4k

点赞数 3

CC 4.0 BY-SA版权

分类专栏：数据结构与算法

本文链接：https://blog.youkuaiyun.com/qq_19782019/article/details/82759650

数据结构与算法专栏收录该内容

39 篇文章

订阅专栏

本文介绍了有权图的基本概念及其两种常见的数据结构表示方法——邻接矩阵和邻接表，并详细阐述了在这两种表示方法中如何具体实现边的权值。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

有权图

前言

在前面一次讨论中，我们知道了无权图如何进行深度遍历以及广度遍历。但是，在现实生活中，图大多数都是“有权图”，即节点与节点之间的边上存在一定的“权值”。通常这个“权值”一般是数字，比如下图这张“有权图”：

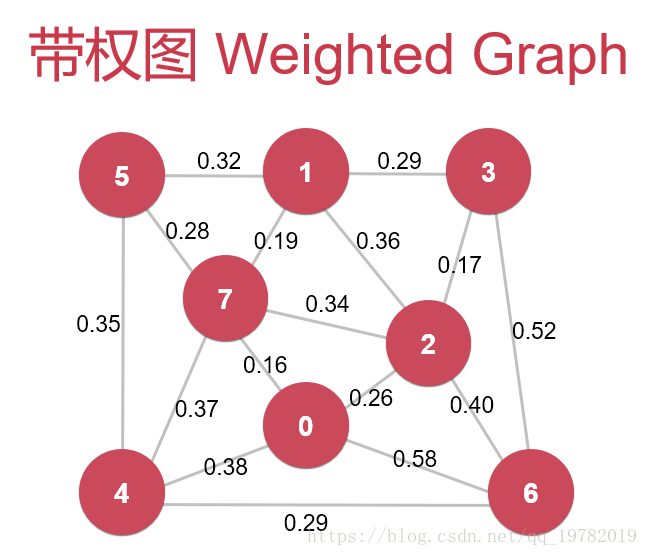
其中，边上面的数字就是所谓的“权值”，例如，我们可以把这张图看做不同的几个城市，边上数值代表着两城市之间的距离。但是“权值”也不仅仅只能用数组表示，也可能是一些其他的数据结构，其中存储着更为复杂的信息。

带权图的数据结构

我们知道，图有两种表示表示方法：1.邻接矩阵表示法和2.邻接表表示法。前面分别使用这两种方法描述了无权图，那么用这两种方法再来描述“有权图”有没有什么差别呢？

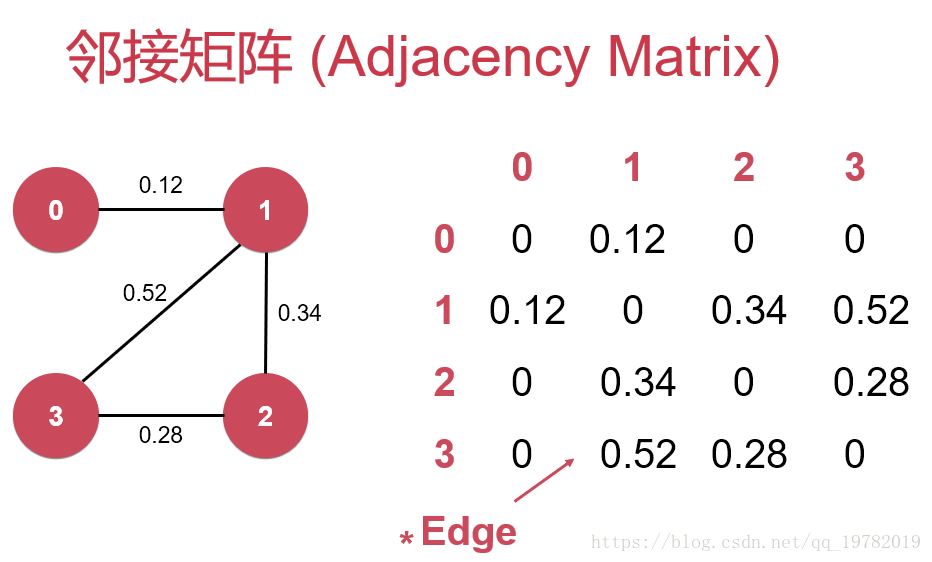
对于邻接矩阵来说，我们只需要进行如下改造即可：

即把原来的bool类型改为具体的权重类型，在这里我们的权重用double类型来表示，比如0与1节点之间的权重查邻接矩阵为0.12，这样就能很容易的知道任意两个节点之间的权重了。

这样看上去貌似很容易就实现了“有权图”，但是我们再来看看用邻接表实现“有权图”又会是怎样呢？

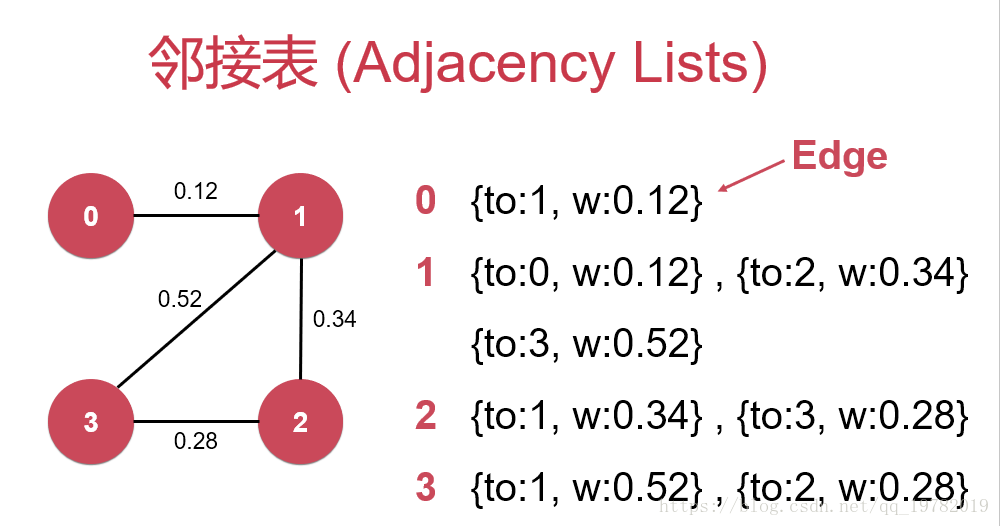
因为邻接表不像邻接矩阵一样是通过节点之间的布尔值来判断是否相连，因此为了能够表达出“权值”，在邻接表中，每个节点的右边由节点要变成带有权值的边，因此我们需要再设计一个数据结构Edge给抽象出边的表示，这样才能解决邻接表无法表现边“权值”的问题。Edge主要包含了两个节点的数值以及这两节点之间边上的权值。因此，为了统一，我们给邻接矩阵也加上Edge这个数据结构，如下图所示：

边Edge的结构设计

首先，边的数据结构Edge需要储存的相关数据有1.边是哪两个节点之间组成的边？2.边上的权值大小是多少？

因此，Edge的基础字段如下：

class Edge {
private:
    int a, b;//分别为边的两个端点
    Weight weight;//两端点之间边的权重

Edge的构造函数如下：

public:
    Edge(int a, int b, Weight weight) : a(a), b(b), weight(weight) {}

Edge对外提供的接口如下：

 int V() {//返回第一个端点
        return a;
    }

    int W() {//返回第二个端点
        return b;
    }

    Weight wt() {//返回边的权值
        return weight;
    }

此外，还提供一个重要的方法，接收一个节点，返回这条边上的另一个节点的方法，这将在后面有重要的作用：

 int other(int x) {//返回给定端点的另一个端点
        return x == a ? b : a;//若x为a,则返回b;若x为b则返回a
    }

剩下的就是输出边的信息使用的方法：

 // 输出边的信息
friend ostream &operator<<(ostream &os, const Edge &e) {
    os << e.a << "-" << e.b << ": " << e.weight;
    return os;

邻接矩阵的结构改造

首先对于邻接矩阵表示的图来说，其基本的结构如下：

template<typename Weight>
class DenseGraph {//构建稠密图类，使用邻接矩阵法表示
private:
    int n, m;//n为图的顶点数量，m为边的数量
    bool directed;//是否为有向图
    vector<vector<Edge<Weight> *>> g;//构建二维数组g作为邻接表的结构基础，其存储类型为布尔类型

其中，对于描述图的基础结构，我们依然使用了二维Vector向量来表示，但是向量中存储的类型变为了Edge的指针，之所以使用指针是因为如果两点之间不存在边Edge,则可用NULL空指针来代替。

其构造函数如下所示：

 DenseGraph(int n, bool directed) {//构造函数
        this->n = n;
        this->directed = directed;
        this->m = 0;
        //下面为初始化n*n的矩阵，每一个g[i][j]指向一个Edge，即一条边的信息
        g = vector<vector<Edge<Weight> *>>(n, vector<Edge<Weight> *>(n, NULL));

    }

添加新边的方法也必须相应的修改，如果添加一条已经存在的边，则执行覆盖操作，删除原来的边，加入新边：

 void addEdge(int v, int w, Weight weight) {//在v节点和w节点之间建立连接关系
        assert(v >= 0 && v < n);
        assert(w >= 0 && w < n);//防止数组越界访问
        if (hasEdge(v, w)) {//若重复连边，则进行替换操作，删除原来的边信息，重置边信息
            delete g[v][w];
            if (v != w && !directed) {//如果为无向图，则另一对边信息也需要删除
                delete[] g[w][v];
            }
            m--;
        }
        //添加一个新边
        g[v][w] = new Edge<Weight>(v, w, weight);
        //如果是无向图的话另一条边也要加上去
        if (v != w && !directed) {
            g[w][v] = new Edge<Weight>(w, v, weight);
        }
        m++;

    }

在图中最为重要的迭代器也需要做一定的修改，比如返回类型不能再是单纯的返回相邻节点序列号了，而应该是与之相邻的边Edge的指针：

 public:
        adjIterator(DenseGraph &graph, int v) : G(graph) {//生成一个迭代器的构造函数
            assert(v >= 0 && v < G.n);
            this->index = -1;
            this->v = v;
        }

        ~adjIterator() {};

//因为邻接矩阵结构的特殊性，即邻接矩阵中的一个节点其关联链表中的元素并不是都有效
        //必须值为true才有效，因此并不能保证直接从第一个元素开始访问，所以index初始化为-1
        Edge<Weight> *begin() {
            index = -1;
            return next();
        }

        Edge<Weight> *next() {
            for (index += 1; index < G.V(); index++) {
                if (G.g[v][index] == true) {//只把真正有效的元素返回出去
                    return G.g[v][index];
                }
            }
            return NULL;
        }

        bool end() {
            return index >= G.V();//判断是否遍历完成
        }

    };

邻接表的结构改造

对于邻接表来说，与邻接矩阵的改变差不多是相同的，只不过原来每个节点后都跟着一群与之相邻的节点，现在变成了一群与之相邻的边Edge,更确切的来说是一群指向Edge的指针。

邻接表的构造函数如下：

template<typename Weight>
class SparseGraph {//构建稀疏图，并使用邻接表结构
private:
    int n, m;//n为图的节点数量,m为图的边数量
    bool directed;//表示图是否为有向图
    vector<vector<Edge<Weight> *>> g;//使用二维数组来表示邻接表,且数据类型为int类型

添加边与判断边的方法分别如下：

//在v与w节点之间加上一条边
    void addEdge(int v, int w, Weight weight) {
        assert(v >= 0 && v < n);
        assert(w >= 0 && w < n);//防止越界
        //由于邻接表的特殊性，相比邻接矩阵来说，查询是否加入的为重边需要遍历整个链表
        //为提高效率，在此处允许加入重边
        g[v].push_back(new Edge<Weight>(v, w, weight));//在v的邻接表中加入w节点
        if (v != w && !directed) g[w].push_back(new Edge<Weight>(w, v, weight));//v与w不是同一个节点
        // 且图不是有向图，才需要执行改该步骤
        m++;
    }

    bool hasEdege(int v, int w) {//判断v节点与w节点之间是否存在边
        assert(v >= 0 && v < n);
        assert(w >= 0 && w < n);
        for (int i = 0; i < g[v].size(); i++) {//遍历与v节点相连的节点
            if (g[v][i]->other(v) == w) return true;//查找与g[v]所有Edge中除节点V的另一个节点是否为w
            // ，则表明v节点与w节点之间已经存在边
        }
        return false;
    }


    void show() {

        for (int i = 0; i < n; i++) {
            cout << "vertex " << i << ":\t";
            for (int j = 0; j < g[i].size(); j++)
                cout << "( to:" << g[i][j]->w() << ",wt:" << g[i][j]->wt() << ")\t";
            cout << endl;
        }
    }

同样，对于迭代器来说，返回的也不仅仅是节点了，而是与之相连所有的边。

class adjIterator {//构建稀疏图迭代器
    private:
        SparseGraph &G;//存储图的引用
        int v;
        int index;//index起指示作用，指向目前迭代器正在访问的节点
    public:
        adjIterator(SparseGraph &graph, int v) : G(graph) {//传入图的引用以及需要遍历的节点
            this->v = v;
            this->index = 0;
        }

        ~adjIterator() {

        }

        Edge<Weight> *begin() {
            index = 0;
            if (G.g[v].size())//如果需要遍历的图中的v节点存在着邻边，则返回邻边表中的第一个值
                return G.g[v][index];
            return NULL;
        }

        Edge<Weight> *next() {//从当前迭代的元素向下一个元素移动
            index++;
            if (index < G.g[v].size())//确保访问时不会发生越界
                return G.g[v][index];//返回需要的元素
            return NULL;
        }

        bool end() {//判断迭代是否要结束了
            return index >= G.g[v].size();//目前访问的节点的索引没有
            // 超过邻边表中的最大索引值，则没结束
        }
    };